



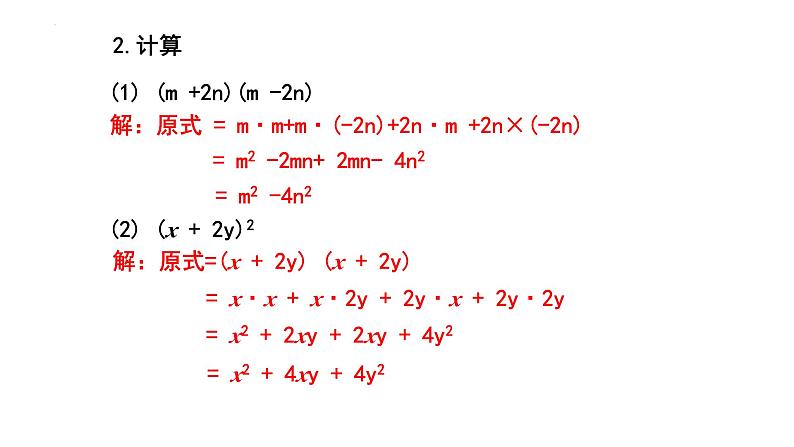
北师大版(2024)七年级下册(2024)第一章 整式的乘除4 整式的除法集体备课课件ppt
展开
这是一份北师大版(2024)七年级下册(2024)第一章 整式的乘除4 整式的除法集体备课课件ppt,共17页。PPT课件主要包含了多项式乘多项式,第一章整式的乘除,a+bm+n,+an,+bm,+bn等内容,欢迎下载使用。
1.4.3 整式的乘法
北师大版七年级数学下册
1、理解多项式乘多项式法则;
2、会利用多项式乘法法则进行计算.中考考点:多项式与多项式相乘
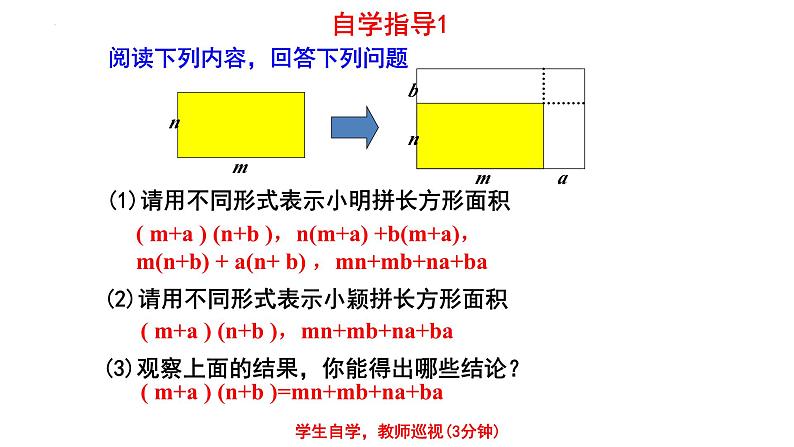
阅读下列内容,回答下列问题
(1)请用不同形式表示小明拼长方形面积
(2)请用不同形式表示小颖拼长方形面积
学生自学,教师巡视(3分钟)
(3)观察上面的结果,你能得出哪些结论?
( m+a ) (n+b ),n(m+a) +b(m+a),m(n+b) + a(n+ b) ,mn+mb+na+ba
( m+a ) (n+b ),mn+mb+na+ba
( m+a ) (n+b )=mn+mb+na+ba
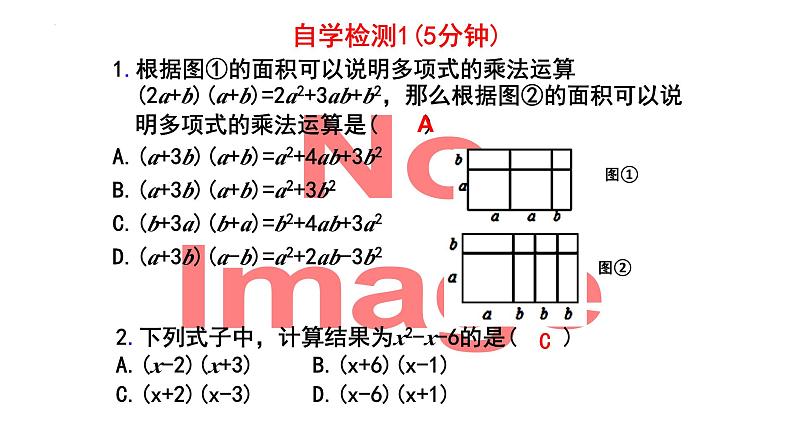
1.根据图①的面积可以说明多项式的乘法运算(2a+b)(a+b)=2a2+3ab+b2,那么根据图②的面积可以说明多项式的乘法运算是( )A.(a+3b)(a+b)=a2+4ab+3b2B.(a+3b)(a+b)=a2+3b2C.(b+3a)(b+a)=b2+4ab+3a2D.(a+3b)(a-b)=a2+2ab-3b2
2.下列式子中,计算结果为x2-x-6的是( )A.(x-2)(x+3) B.(x+6)(x-1)C.(x+2)(x-3) D.(x-6)(x+1)
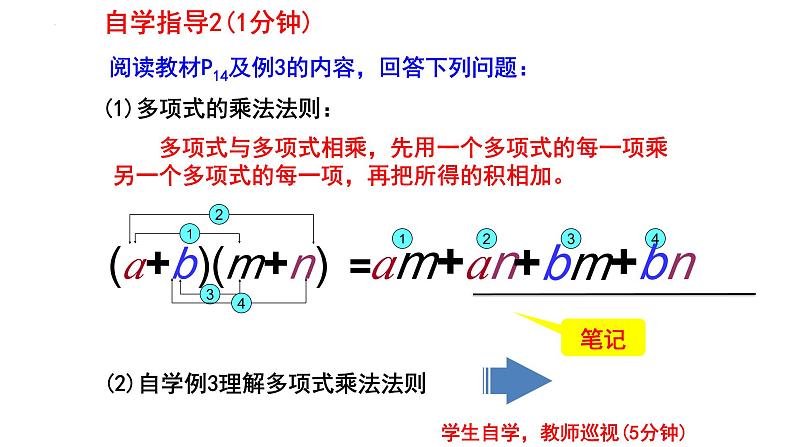
阅读教材P14及例3的内容,回答下列问题:
(2)自学例3理解多项式乘法法则
学生自学,教师巡视(5分钟)
(1)多项式的乘法法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加。
(2) (x + 2y)2
3.如果(x-2)(x+1)= x2 + mx + n,求 m + n的值.
(1) (m+2n)(m-2n)
解:原式 = m·m+m·(-2n)+2n·m +2n×(-2n)
= m2 -2mn+ 2mn- 4n2
解:原式=(x + 2y) (x + 2y)
= x·x + x·2y + 2y·x + 2y·2y
= x2 + 2xy + 2xy + 4y2
= x2 + 4xy + 4y2
(1) (m +2n)(m -2n)
分析:根据多项式乘多项式法则把等式的左边展开,根据题意求出m、n的值,计算即可。
= x·x + x·1 + (-2)·x + (-2)×1
= x2 + x – 2x - 2
= x2– x - 2
∴ m = -1 n = -2
∴ m + n =(-1)+(-2)= -3
故 m + n 的值为-3.
∵ x2 + mx + n = x2– x - 2
讨论、更正、点拨(5分钟)
多项式乘以多项式要注意什么?
分析:先弄清楚两个多项式中的每一项
分析:先将(x + 2y)2变式为(x + 2y) (x + 2y)
注意每一项的符号,特别是负号时不要遗漏
结果有同类项的要合并同类项
1.多项式的乘法法则:
2.多项式乘以多项式要注意:
(1)注意每一项的符号,特别是负号时不要遗漏;
(2)结果有同类项的要合并同类项。
2.若(y+3)(y-2)=y²+my+n,则m= ,n= .
1.若(x+m)(x-8)中不含x的一次项,则m的值为( )A.8 B.-8 C.0 D.8或-8
(变式)若(x-3)(x2+ax+b)的积中不含x的二次项和一次项,则a和b的值( )A.a=0;b=2 B.a=3;b=9C.a=-1;b=2 D.a=2;b=4
(2) (-2m-1)(3m-2)
(1) (x+y)(a+2b)
(3) (-2x+3)2
(变式)若(x+3)(x+n)=x2+mx-15,则m的值为( ) A.-5 B.-2 C.5 D.2
解:原式= x·a + x·2b + y·a + y·2b
= ax + 2bx + ay + 2by
解:原式= -2m·3m – 2m·(-2) -1×3m -1×(-2)
= -6m²+ 4m–3m +2
= -6m² + m +2
解:原式=(-2x + 3) (-2x + 3)
= (-2x)·(-2x) + (-2x)·3 + 3·(-2x) + 3×3
= 4x2 - 6x – 6x + 9
= 4x2 – 12x + 9
4.已知a+b=m,ab=-4,求(a-2)(b-2)的值.
解:原式= a·b + a·(-2) + (-2)·b + (-2)×(-2) = ab–2a - 2b + 4 = ab –2(a+b) + 4
当 a + b = m,ab = -4 时,原式= (-4) – 2m + 4 = -2m
5.关于y的代数式(y-n)(y+8)的积中的常数项为16,则n的值为多少?
解:(y-n)(y+8) = y·y + y·8 + (-n)·y + (-n) ·8 = y² + 8y –ny - 8n = y² + (8–n)y - 8n
即常数项为-8n,则 -8n = 16解得 n = -2 故n的值为-2.
(选做题) (课本P17习题1.2 第8题)
计算(a+b+c)(c+d+e)
解:方法一:(a+b+c)(c+d+e)
= (a+b+c)c+(a+b+c)d+(a+b+c)e= ac+bc+c²+ad+bd+cd+ae+be+ce 方法二: (a+b+c)(c+d+e)= (c+d+e)a+ (c+d+e)b+ (c+d+e)c=ca+da+ea+cb+db+eb+c2+dc+ec
分析:运用整体思想:把(a+b+c)看成整体或把(c+d+e)看成整体,再运用乘法分配律最后得到结果.
相关课件
这是一份初中数学北师大版七年级下册4 整式的乘法授课课件ppt,共27页。PPT课件主要包含了学习目标,情境导入,①不能漏乘,探究新知,多项式乘多项式,+mb,+an,+ab,归纳总结,多项式与多项式相乘等内容,欢迎下载使用。
这是一份初中数学北师大版七年级下册第一章 整式的乘除4 整式的乘法教学演示课件ppt,共27页。PPT课件主要包含了学习目标,情境导入,①不能漏乘,探究新知,多项式乘多项式,+mb,+an,+ab,归纳总结,多项式与多项式相乘等内容,欢迎下载使用。
这是一份北师大版七年级下册4 整式的乘法课堂教学课件ppt,共19页。PPT课件主要包含了a+bm+n,+an,+bm,+bn,-06•x,x•x,两项相乘时先定符号,-2x•y,+y•x,y•y等内容,欢迎下载使用。









