初中数学第9章 轴对称、平移与旋转9.3 旋转3.旋转对称图形示范课课件ppt

这是一份初中数学第9章 轴对称、平移与旋转9.3 旋转3.旋转对称图形示范课课件ppt，共35页。PPT课件主要包含了旋转的特征，对应线段相等，对应角相等，旋转对称图形的画法，旋转对称图形等内容，欢迎下载使用。
旋转前后图形相同线：每对对应点到旋转中心的 距离相等角：旋转角彼此相等
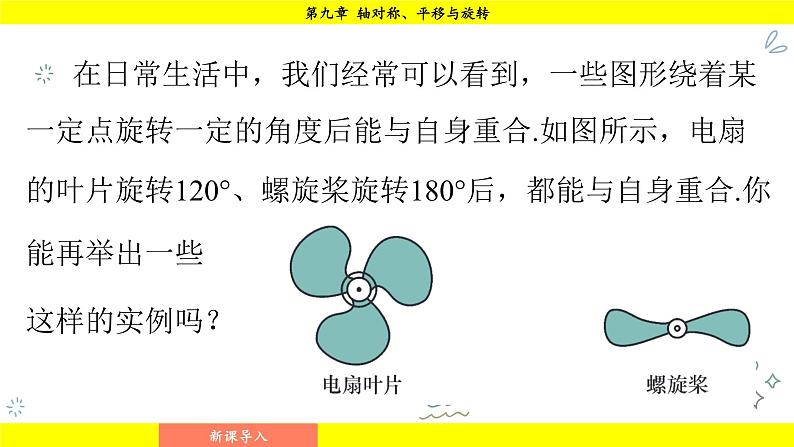
在日常生活中，我们经常可以看到，一些图形绕着某一定点旋转一定的角度后能与自身重合.如图所示，电扇的叶片旋转120°、螺旋桨旋转180°后，都能与自身重合.你能再举出一些这样的实例吗？
用一张半透明的薄纸，覆盖在如图所示的图形上，在薄纸上画这个图形，使它与如图所示的图形重合.然后用一枚图钉在圆心处穿过，将薄纸绕着图钉旋转，观察旋转多少度（小于周角）后，薄纸上的图形能与原图形再一次重合.
由上述操作可知，该图形绕圆心旋转60°后，能与自身重合（绕圆心旋转120°、180°、240°或300°后，也能与自身重合）.像这样旋转一定角度后能与自身重合的图形叫做旋转对称图形.
旋转对称图形顺时针或逆时针旋转一定角度后，均能与原图形重合，因此可淡化旋转方向.旋转角度可以在0°到360°之间.
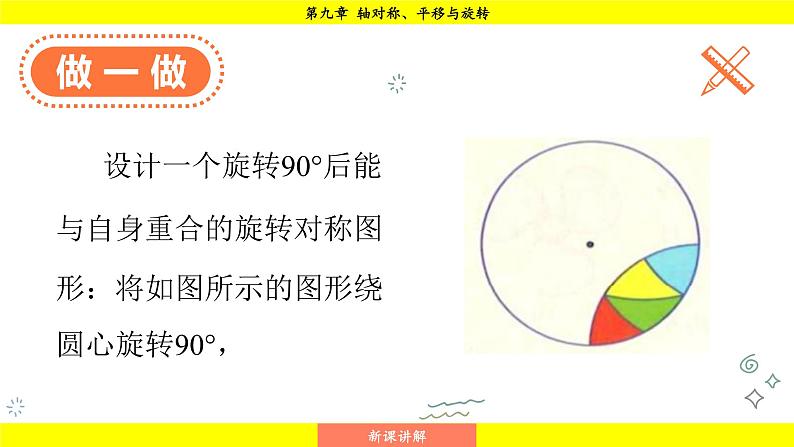
设计一个旋转90°后能与自身重合的旋转对称图形：将如图所示的图形绕圆心旋转90°，
再将旋转后所得到的图形绕圆心旋转90°，然后再重复旋转一次，可以得到如图所示的图形.
将上面的图形绕圆心旋转90°后，可以发现旋转以后的图形能与原来位置上的原图形重合，因此该图形是旋转对称图形.当然该图形绕圆心旋转180°或270°后的图形也能与原图形重合，也可得出该图形是旋转对称图形.你能设计一个旋转30°后能与自身重合的图形吗？
旋转对称图形的定义：在平面内，将一个图形绕着一定点旋转一定角度（小于周角）后能与自身重合的图形叫做旋转对称图形.旋转的度数称为旋转角度.一般来说，旋转角度可以多个，但旋转中心只有一个.
下列各图形是不是旋转对称图形？如果是，请找出旋转中心、旋转角度.这些图形是轴对称图形吗？
(1) 如果一个图形既是旋转对称图形，又是轴对称图形，那么它的旋转中心就是对称轴的交点；
(2) 正 n 边形既是旋转对称图形，又是轴对称图形，所以它的旋转中心就是对称轴的交点，并且旋转角度就等于 360°除以 n 所得的商.
下列图形是旋转对称图形吗？如果是，旋转中心在哪里？旋转角度是多少？再想一想它们是轴对称图形吗？
三个图形都是旋转对称图形，也都是轴对称图形；它们的旋转中心为对称轴的交点；最小旋转角分别为 60°，72°，90°.
思考：旋转对称图形与以前学过的轴对称图形相同吗？1. 旋转对称图形与轴对称图形是两种不同的对称图形，旋转对称图形不一定是轴对称图形，轴对称图形不一定是旋转对称图形，它们是两个不同的概念.2. 旋转对称图形是旋转一定的角度得到，轴对称图形是翻折得到.
如下图是某一种花的花瓣和中心，现以 O 为旋转中心画出分别旋转 45°， 90°，135°，180°， 225°， 270°，315°的这种花的图形。
1. 任意定一点旋转中心 O；
2. 按设计需要，把周角 360°分成 n 等份；
3. 以 O 为旋转中心，360°除以 n 的商为旋转角做顺时针或逆时针旋转 n-1次即可得到一个旋转对称图形.
古建筑中的旋转对称——从敦煌洞窟到欧洲教堂敦煌的佛教洞窟与欧洲的基督教堂相距数千千米，文化和宗教背景截然不同，然而，在相距几百年的时间里，却先后出现了完全相同的一种图案：三只兔子相互追逐
形成一环.大英博物馆《国际敦煌学项目》首次披露了这一新发现.
敦煌佛教洞窟中，至少有16个洞窟中出现了这一图案：三只兔子位于莲花的中心，耳朵相连，朝着不同方向，互相追逐，有的是顺时针（如305窟），有的是逆时针（如407窟）.这些洞窟建于隋朝和晚唐时期.但是，敦煌学文献中却找不到关于这一图案相关研究的记录.
而到了13世纪，在欧洲的德国、法国和英国某些基督教堂的屋顶浮雕等处，都发现了相同或相似的图案.
这三只兔子是如何从中国传到欧洲的，一时成为敦煌学界的一大研究热点.有专家指出，这一图案是通过中国的纺织品经由丝绸之路传到欧洲的，但目前还没有确切的证据证实这一观点.对此，专家们还在进行研究，以期解开“三只兔子之谜”.
1.举出日常生活中旋转对称图形的几个实例.
2.找找看，下面这幅古代艺术品图形中有几匹马？它们的位置关系大致如何？
3.如图所示的图形绕哪一点旋转多少度后能与自身重合？（1） （2）
4.任意作一个△ABC，再任意作一个点P，然后作出△ABC绕点P逆时针旋转60°后的三角形.
1. 下列英文字母属于旋转对称图形的是 ( )
A B C D
2. 下列图形中，绕旋转中心旋转 60°后能与自身 重合的是 ( )
3. 下列各个说法正确的是 ( ) A. 是旋转对称图形，肯定不是轴对称图形 B. 是轴对称图形，肯定是旋转对称图形 C. 一些图形可能既是旋转对称图形，又是轴对 称图形
4. 在梯形、正三角形、等腰三角形、正方形、线段、正六边形、圆中，是旋转对称图形的是 .
正三角形、正方形、线段、正六边形、圆
定义与轴对称图形的区别画法
定义：在平面内，将一个图形绕着一定点旋转一定角度（小于周角）后能与自身重合的图形叫做旋转对称图形.旋转的度数称为旋转角度.一般来说，旋转角度可以多个，旋转中心只有一个.
与轴对称图形的区别：1. 是两种不同的对称图形，旋转对称图形不一定是轴对称图形，轴对称图形不一定是旋转对称图形，它们是两个不同的概念.2. 旋转对称图形是旋转一定的角度得到，轴对称图形是翻折得到.
2. 按设计需要，把周角 360°分成n等份；