华师大版七年级下册3 旋转对称图形一等奖ppt课件

这是一份华师大版七年级下册3 旋转对称图形一等奖ppt课件，文件包含1033旋转对称图形pptx、1033旋转对称图形教学设计doc、1033旋转对称图形学案doc等3份课件配套教学资源，其中PPT共27页， 欢迎下载使用。

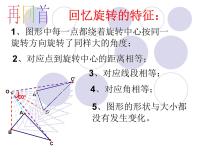
图形旋转的特征是什么?
图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状与大小不变.
在日常生活中,我们经常可以看到,一些图形绕着某一定点旋转一定的角度后能与自身重合.如图所示,电扇的叶片旋转120°、螺旋桨旋转180°后,都能与自身重合.
你能再举出一些这样的实例吗?
用一张半透明的薄纸,覆盖在如图所示的图形上,在薄纸上画这个图形,使它与如图所示的图形重合.
然后用一枚图钉在圆心处穿过,将薄纸绕着图钉旋转,观察旋转多少度(小于周角)后,薄纸上的图形能与原图形再一次重合。
若顺时针或逆时针旋转一定角度,该图形都能与原图形重合,则可以淡化旋转方向。
由上述操作可知,该图形绕圆心旋转60°后,能与自身重合,而且绕圆心旋转120°或180°后,都能与自身重合。
像这样旋转一定角度后能与自身重合的图形就称为旋转对称图形.
用类似上述的操作方法对如图所示的图形进行探索,看看它是不是旋转对称图形.
若是,想一想旋转中心在何处,需要旋转多少度后,能与自身重合.该图形还是轴对称图形吗?
这是一个旋转对称图形.旋转中心是正方形对角线的交点.绕着中心顺时针或逆时针旋转90°或180°后，能与自身重合.但它不是轴对称图形.
下图所示的图形是轴对称图形.用类似上述的操作方法对下图所示的图形进行探索,它能通过旋转与自身重合吗?
这是一个轴对称图形，同时也是一个旋转对称图形.绕着它的中心旋转180°后，可以与自身重合.
易错点：旋转对称图形不一定都是轴对称图形，也不是所有的轴对称图形都是旋转对称图形，它们都是具有特殊性质的图形。如果一个图形既是旋转对称图形，又是轴对称图形，那么它的旋转中心就是对称轴的交点。
你能设计一个旋转30°后能与自身重合的图形吗?
正十二边形，除了旋转30°，还有旋转多少度能与自身重合的图形呢?
1. 一个旋转对称图形旋转的角度可能不止一种．2. 旋转角不确定时，先在0°～360°范围内找出其旋转后能与自身重合的最小角度，那么这一图形旋转这一最小角度的整数倍数后均与原图形重合．
如图,画△ABC和过点P的两条直线PQ、PR.画出△ABC关于PQ对称的三角形A'B'C',再画出△A'B'C'关于PR对称的三角形A"B"C".
观察△ABC和△A"B"C”,你能发现这两个三角形有什么关系吗?
△A"B"C”是由△ABC绕点P旋转得到的。
1、2022年2月4日-2月20日，北京冬奥会隆重举行，如图是在北京冬奥会会徽征集过程中征集到的一幅图片．旋转图片中的“雪花图案”，旋转后要与原图形重合，至少需要旋转( )A.180° B.120° C.90° D.60°
解：360°÷6=60°该图形绕中心至少旋转度后能和原来的图案互相重合．故选：D．
2、下列四个圆形图案中，分别以它们所在圆的圆心为旋转中心，顺时针旋转120°后，能与原图形完全重合的是（ ）   
A. B. C. D.
解：A、最小旋转角度360°÷3=120°B、最小旋转角度360°÷4=90°;C、最小旋转角度360°÷2=180°;D、最小旋转角度360°÷5=72°;综上可得:顺时针旋转120°后，能与原图形完全重合的是A.
3、如图所示的正六边形花环绕中必至少旋转α度能与自身重合，则α为（ ）A. 30 B.60 C.120 D.180
解:该图形围绕自己的旋转中心，至少针旋转360°÷6=60°后，能与其自身重合．故选：B．
如果一个图形既是旋转对称图形，又是轴对称图形，那么它的旋转中心就是对称轴的交点。正n边形既是旋转对称图形，又是轴对称图形，所以它的旋转中心就是对称轴的交点，并且旋转角度就等于360°除以n所得的。
10.3.3 旋转对称图形
1、定义2、旋转中心与旋转角