初中数学浙教版（2024）七年级下册（2024）1.1 直线的相交优质课件ppt

这是一份初中数学浙教版（2024）七年级下册（2024）1.1 直线的相交优质课件ppt，共30页。PPT课件主要包含了教学目标，垂线段等内容，欢迎下载使用。
理解垂线、垂线段等概念
能用三角尺或量角器过一点画已知直线的垂线
掌握基本事实：在同一平面内，过一点有且只有一条直线与已知直线垂直
理解点到直线的距离的意义，能度量点到直线的距离
把一张正方形纸片按图折叠，就得到一个角∠1。∠1是什么角？
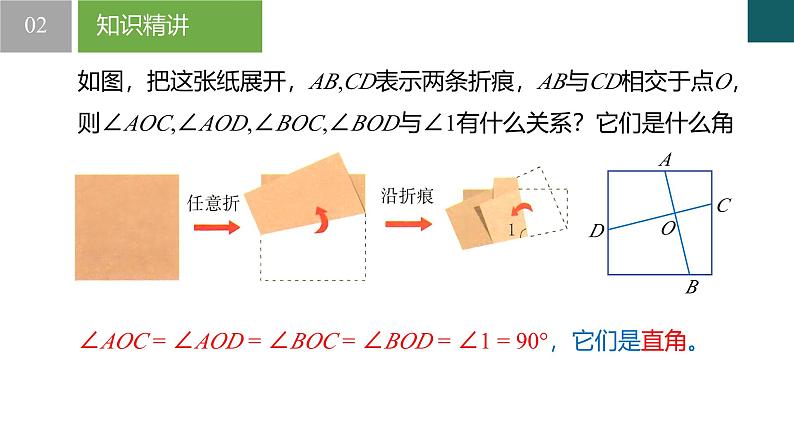
如图，把这张纸展开，AB,CD表示两条折痕，AB与CD相交于点O，则∠AOC,∠AOD,∠BOC,∠BOD与∠1有什么关系？它们是什么角？
∠AOC = ∠AOD = ∠BOC = ∠BOD = ∠1 = 90°，它们是直角。
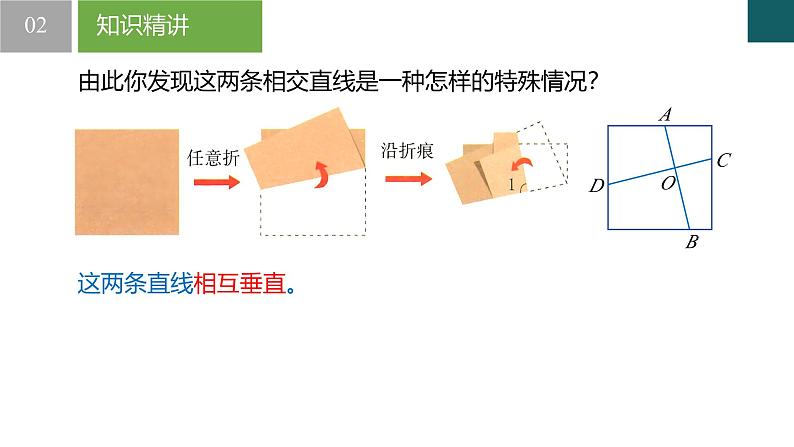
由此你发现这两条相交直线是一种怎样的特殊情况？
互相垂直、垂线、垂足： 当两条直线相交所构成的四个角中有一个是直角时， 我们就说这两条直线互相垂直， 其中的一条直线叫作另一条直线的垂线， 它们的交点叫作垂足。
在生活中，你能找到哪些可看成两条直线互相垂直的例子？
墙、门、黑板、课桌、书本等的相邻两边。
垂直是相交的一种特殊情况。
如图，直线AB与CD垂直，记作AB⊥CD ( 或CD⊥AB )。如果用l,m分别表示这两条直线，那么直线l与m垂直，记作l⊥m。交点O是垂足。
图左和图右分别表示用三角尺和量角器过直线l外一点A画直线l的垂线的方法。
当点A在直线l上时，可以怎么画？
如图，A是直线l上一点，B是直线l外一点。分别过点A,B画直线l的垂线。这样的垂线能画几条？( 请与你的同伴交流 )
基本事实： 一般地， 在同一平面内，过一点有且只有一条直线与已知直线垂直。
公理详解：( 1 ) 在同一平面内是前提；( 2 ) 过一点可以是过已知直线外一点，也可以是过已知直线上一点。
若缺少了“在同一平面内”这一前提，会出现怎样的情况？
直线b和c都符合要求，即过一点不止有一条直线与已知直线垂直。
如图，过点P作直线a的垂线。
例3 如图，直线AB与直线CD相交于点O，OE⊥AB。已知∠BOD = 45°，求∠COE的度数。
解：∵OE⊥AB，∴∠AOE = 90°( __________ )。又∵∠AOC与∠BOD是对顶角，根据“对顶角相等”，得∠AOC = ∠BOD = 45°，∴∠COE = ∠AOC + ∠AOE = 45° + 90° = 135°。
如图，过点P作线段AB的垂线，垂足在（　　）A．线段AB上 B．线段AB的延长线上C．线段AB的反向延长线上 D．直线AB外
如图，直线AB与直线CD相交于点O，EO⊥AB，∠EOD = 25°，则∠AOC = __________。
∵EO⊥AB，∴∠AOE = 90°，∴∠AOC = 180° - 25° - 90° = 155° - 90° = 65°。
已知三条射线OA，OB，OC，OA⊥OC，∠AOB = 60°，则∠BOC = ____________。
如图1，∵OA⊥OC，∴∠AOC=90°，∴∠BOC = ∠AOC - ∠AOB = 90° - 60° = 30°；
如图2，∵OA⊥OC，∴∠AOC=90°，∴∠BOC = ∠AOC + ∠AOB = 90° + 60° = 150°；综上，∠BOC的度数为30°或150°。
如图，P是直线l外一点，画PO⊥l于点O，线段PO称为点P到直线l的垂线段。点P与直线l上所有各点之间的距离中，哪一个距离最小？请设计一个实验来验证。( 请与你的同伴交流 )
用直尺分别测量PO、PA1、PA2、PA3、PB1、PB2、PB3的长度，可知：PO距离最小。
垂线段： 一般地， 连结直线外一点与直线上各点的所有线段中，垂线段最短。点到直线的距离： 从直线外一点到这条直线的垂线段的长度， 叫作点到直线的距离。
eg：如图，垂线段PO的长度就是点P到直线l的距离。
课内练习 1. 如图，CD⊥EF，∠1=∠2，则AB⊥EF。解：∵CD⊥EF，根据_________________，∴∠1 = _________，∵∠2 = ∠1 = _________，根据_________________，所以AB_____EF。
课内练习 2. 如图，工人师傅常用角尺来画工件边缘的垂线。你能说明其中的理由吗？
角尺的两条边是互相垂直的，可以用它画互相垂直的直线。
课内练习 3. 如图，P是∠AOB内的一点。画出点P到∠AOB两边的垂线段。
例1、如图，计划把河水引到水池A中，可以先引AB⊥CD，垂足为B，然后沿AB开渠，则能使所开的渠最短，这样设计的依据是（　　）A．垂线段最短B．两点之间线段最短C．两点确定一条直线D．过两点有且只有一条直线
( 1 ) 如图，AC⊥BC，CD⊥AB，垂足分别为C、D，线段CD的长度是（　　）A．点A到BC的距离B．点B到AC的距离C．点C到AB的距离D．点D到AC的距离
( 2 ) 如图，AC⊥BC于点C，CD⊥AB于点D，图中能用现有字母表示的线段中，长度能表示点到直线 ( 或线段 ) 的距离的线段有________条。
如图，线段BC的长是点B到AC的距离，线段AC的长是点A到BC的距离，线段CD的长是点C到AB的距离，线段BD的长是点B到CD的距离，线段AD的长是点A到CD的距离，故图中能表示点到直线距离的线段共有5条。
( 1 ) 点P为直线m外一点，点A，B，C为直线m上三点，PA = 4cm，PB = 5cm，PC = 2cm，则点P到直线m的距离为（　　）A．4cm B．2cmC．小于2cm D．不大于2cm
( 2 ) 如图，CD⊥AB，垂足是点D，AC = 8，BC = 6，CD = 4，点E是线段AB上的一个动点 ( 包括端点 )，连接CE，那么CE的长为整数值的线段有（　　）A．3条B．8条C．7条D．5条
∵CD⊥AB，垂足是点D，AC = 8，BC = 6，CD = 4，∴CE长的范围是4 ≤ CE ≤ 8，当点E由A向B运动时，CE的整数值线段长度分别为：8、7、6、5、4、5、6，共7条。
互相垂直、垂线、垂足： 当两条直线相交所构成的四个角中有一个是直角时，我们就说这两条直线互相垂直， 其中的一条直线叫作另一条直线的垂线，它们的交点叫作垂足。
基本事实： 一般地，在同一平面内，过一点有且只有一条直线与已知直线垂直。
垂线段： 一般地，连结直线外一点与直线上各点的所有线段中，垂线段最短。点到直线的距离： 从直线外一点到这条直线的垂线段的长度，叫作点到直线的距离。