2025年九年级中考数学一轮专题复习 平方根综合 课件

这是一份2025年九年级中考数学一轮专题复习 平方根综合 课件，共38页。PPT课件主要包含了知识点1算术平方根，知识点1平方根，±25，解1±3，±19等内容，欢迎下载使用。
题组一: 算术平方根、平方根的计算
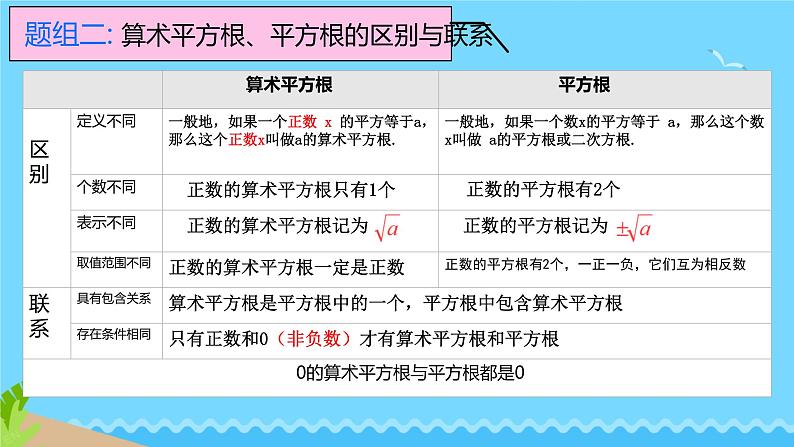
题组二: 算术平方根、平方根的区别与联系
1．下列说法正确的是（ ）A．9的算术平方根是－3 B． 16的算术平方根是4C．－16的算术平方根是－4 D．－9的算术平方根是3
2. 已知x有算术平方根，则x的取值范围是（ ） A、x≥0； B、x＜0； C、x≥1； D、x＞0.
9．下列说法正确的是（ ）A．4的平方根是2 B．4的算术平方根是-2 C．8的平方根是4 D．9的平方根是
12、若一个正数的算术平方根是a，则比这个数大3的正数的平方根 是（ ）
13、一个数的平方根是2m+1和m-4，则m=_______，这个数是______.
14、若x+3是4的平方根，则x=________.
18、根据下表回答下列问题：
(1) 268.96的平方根是多少？
4．(南充中考)0.49的算术平方根的相反数是( )A．0.7 B．－0.7 C．±0.7 D．0
7．下列说法正确的是( )A．因为52＝25，所以5是25的算术平方根B．因为(－5)2＝25，所以－5是25的算术平方根C．因为(±5)2＝25，所以5和－5都是25的算术平方根D．以上说法都不对
知识点2　估计算术平方根
10．一个正方形的面积为50平方厘米，则正方形的边长约为( )A．5厘米 B．6厘米 C．7厘米 D．8厘米
知识点3　用科学计算器求一个正数的算术平方根
解：28.284. 0.762. 49.000.
16．设a－3是一个数的算术平方根，那么( )A．a≥0 B．a＞0 C．a＞3 D．a≥3
19．若一个数的算术平方根等于它本身，则这个数是( )A．1 B．－1 C．0 D．0或1
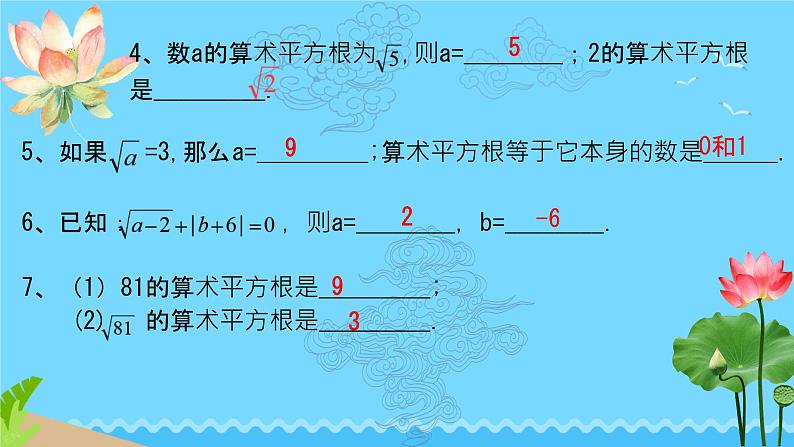
22．若一个数的算术平方根是11，则这个数是__________．
23．若x－3的算术平方根是3，则x＝_______．
29．兴华的书房面积为10.8 m2，她数了一下地面所铺的正方形地砖正好是120块，请问每块地砖的边长是多少？
28．求下列各式中的正数x的值：(1)x2＝(－3)2； (2)x2＋122＝132.
解：x＝3. x＝5.
解：设每块地砖的边长是xm，则有 120x2＝10.8，即x2＝0.09. ∵x>0，∴x＝0.3.答：每块地砖的边长为0.3m.
3．下面说法中不正确的是( )A．6是36的平方根 B．－6是36的平方根C．36的平方根是±6 D．36的平方根是6
1．(黄冈中考)9的平方根是( )A．±3 B．±13 C．3 D．－3
2．(绵阳中考)±2是4的( )A．平方根 B．相反数 C．绝对值 D．算术平方根
4．下列说法正确的是( )A．任何非负数都有两个平方根 B．一个正数的平方根仍然是正数C．只有正数才有平方根 D．负数没有平方根
知识点2　平方根与算术平方根的关系
解：平方根分别是：(1)±5；(2)0；(3)没有平方根；(4)±2.算术平方根分别是：(1)5；(2)0；(3)没有算术平方根；(4)2.
17．如果某数的一个平方根是－6，那么这个数的另一个平方根是______，这个数是_______．
21．已知2a－1的平方根是±3，3a＋b－1的平方根是±4， 求a＋2b的平方根．
解：根据题意，分以下两种情况：①当a－1与5－2a是同一个平方根时，a－1＝5－2a.解得a＝2.此时，m＝12＝1；
22．(1)一个非负数的平方根是2a－1和a－5，这个非负数是多少？
解：根据题意，得(2a－1)＋(a－5)＝0. 解得a＝2.∴这个非负数是(2a－1)2＝(2×2－1)2＝9.
(2)已知a－1和5－2a都是m的平方根，求a与m的值．
②当a－1与5－2a是两个平方根时，a－1＋5－2a＝0.解得a＝4.此时，m＝(4－1)2＝9.综上所述，当a＝2时，m＝1； 当a＝4时，m＝9.
小方家新买了一张边长是1.3米的正方形的桌子，原有边长是1米的两块台布都不适用了，丢掉又太可惜了，小方的姥姥按如图所示的方法，将两块台布拼成一块正方形大台布.请你帮小方的姥姥算一算，这块大台布能盖住现在的新桌子吗?