2025年九年级中考数学一轮专题复习 平行线及其判定节 课件

这是一份2025年九年级中考数学一轮专题复习 平行线及其判定节 课件，共38页。PPT课件主要包含了一“落”，二“靠”，三“推”，四“画”等内容，欢迎下载使用。
问题1:如何判断两条直线是否平行?
画图过程中,什么角始终保持相等?
由此你得出什么样的结论呢?
问题2:用直尺和三角尺画平行线?
平行线的判定方法1： 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单的说：同位角相等,两条直线平行.
几何语言：∵∠1=∠2(已知)∴AB∥CD(同位角相等,两直线平行)
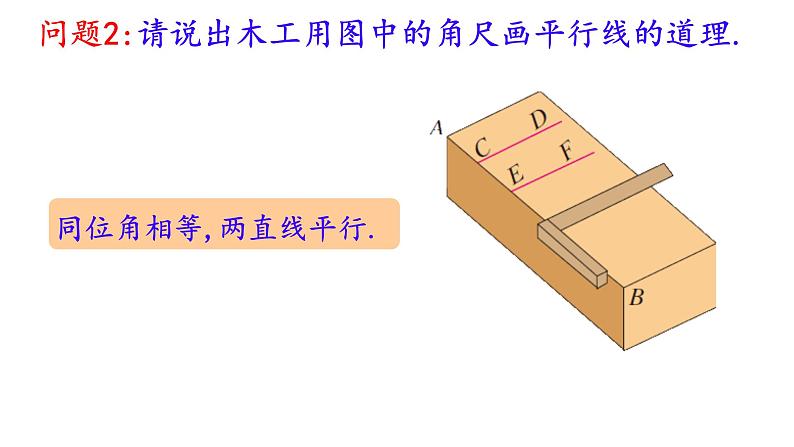
问题2:请说出木工用图中的角尺画平行线的道理.
同位角相等,两直线平行.
问题3:如果两条直线被第三条直线所截,那么能否利用内错角来判定两条直线平行呢?
如图,已知∠3=∠2,求证:a∥b.
证明：∵ ∠2=∠3(已知),∠3=∠1(对顶角相等),∴ ∠1=∠2.∴ a//b(同位角相等,两直线平行）.
平行线的判定方法2： 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单的说：内错角相等,两条直线平行.
几何语言：∵∠2=∠3(已知)∴AB∥CD(内错角相等两直线平行)
问题4:如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢?
如图,已知∠2+∠4=180°,求证:a∥b.
证明：∵∠2+∠4=180° (已知) ∠1+∠4=180° (邻补角的性质)∴∠1=∠2 (同角的补角相等)∴ AB//CD (内错角相等,两直线平行)
平行线的判定方法3： 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单的说：同旁内角互补,两条直线平行.
几何语言：∵∠2+∠4=180°(已知)∴AB∥CD(同旁内角互补,两直线平行)
例：在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?
同一平面内,垂直于同一条直线的两直线平行.
答：这两条直线平行.理由如下：∵ b⊥a， ∴ ∠1= 90°.同理∠2= 90°. ∴∠1=∠2.∵ ∠1和∠2是同位角，∴ b∥c（同位角相等，两直线平行）.
问题5:在铺设铁轨时,两条直轨必须是互相平行的.如图,已经知道∠2是直角,那么再度量图中已标出的哪个角,就可以判断两条直轨是否平行?为什么?
解：①可度量∠3的度数,若∠3=90°,则∠3+∠2=180°.根据“同旁内角互补,两直线平行”可得两条直轨平行.
②也可度量∠4的度数，若∠4=90°,则∠4=∠2.根据“同位角相等,两直线平行”可得两条直轨平行.
③还可度量∠5的度数，若∠5=90°,则∠5=∠2.根据“内错角相等,两直线平行”可得两条直轨平行.
1. 有下列四种说法：①过直线外一点有且只有一条直线与这条直线平行；②同一平面内，过一点能且只能作一条直线与已知直线垂直；③直线外一点与直线上各点连结的所有线段中，垂线段最短；④平行于同一条直线的两条直线互相平行．其中正确的个数是_______个
2. 在同一平面内，若两条直线相交，则公共点的个数是________； 若两条直线平行，则公共点的个数是_________.
3. 若AB∥CD，AB∥EF，则_____∥______，理由是________________.
依据下列语句画出图形已知：点P是∠AOB内一点．过点P分别作直线CD∥OA，直线EF∥OB．
1.在同一平面内两条不重合的直线的 位置关系有( ) A.两种:垂直或相交 B.三种:平行、垂直或相交 C.两种:平行或相交 D.两种:平行或垂直
一、平行公理及推论的应用
2.下列结论正确的是( )A.过一点画已知直线的平行线，能画无数条B.过一点画已知直线的平行线，能画2条C.过一点画已知直线的平行线，最少能画1条D.过一点画已知直线的平行线，最多能画1条
内错角相等，两直线平行。
3.根据条件完成填空。
内错角相等，两直线平行
同旁内角互补，两直线平行
同位角相等，两直线平行
4.在同一平面内，两条直线都垂直于同一 条直线，这两条直线平行吗？为什么？
垂直于同一条直线的两条直线平行
1．(和平区期末)点P，Q都是直线l外的点，下列说法正确的是( ) A．连接PQ，则PQ一定与直线l垂直 B．连接PQ，则PQ一定与直线l平行 C．连接PQ，则PQ一定与直线l相交 D．过点P能画一条直线与直线l平行
2．在同一平面内的两条不重合的直线的位置关系( )A．有两种：垂直或相交； B．有三种：平行，垂直或相交；C．有两种：平行或相交； D．有两种：平行或垂直。
3．在同一平面内，直线a与b满足下列条件，把它们的位置关系填在 后面的横线上。(1)a与b没有公共点，则a与b______；(2)a与b有且只有一个公共点，则a与b______；(3)a与b有两个公共点，则a与b_______．
4．如图，在下面的方格纸中，找出互相平行的线段，并用符号表示 出来：_________________．
CD∥MN，GH∥PN
5．如图，完成下列各题：(1)用直尺在网格中完成：①画出直线AB的一条平行线，②经过C点画直线垂直于CD；(2)用符号表示上面①、②中的平行、垂直关系．
解：(1)如图所示．(2)EF∥AB，MC⊥CD.
6．在同一平面内，下列说法中，错误的是( ) A．过两点有且只有一条直线 B．过一点有无数条直线与已知直线平行 C．过直线外一点有且只有一条直线与已知直线平行 D．过一点有且只有一条直线与已知直线垂直
知识点2　平行公理及其推论
7．若直线a∥b，b∥c，则a∥c的依据是( ) A．平行公理; B．等量代换; C．等式的性质; D．平行于同一条直线的两条直线互相平行。
8．如图，PC∥AB，QC∥AB，则点P，C，Q在一条直线上．理由是_______________________________________________
经过直线外一点，有且只有一条直线与这条直线平行．
9．如图，P，Q分别是直线EF外两点．(1)过P画直线AB∥EF，过Q画直线CD∥EF；(2)AB与CD有怎样的位置关系？为什么？
解：(1)如图．(2)AB∥CD.理由：∵AB∥EF，CD∥EF， ∴AB∥CD.
10．下列说法错误的是( )A．过一点有且只有一条直线与已知直线平行B．平行于同一条直线的两条直线平行C．若a∥b，b∥c，c∥d，则a∥dD．同一平面内，若一条直线与两平行线中的一条相交，那么它也和另一条相交
11．如图，AB∥CD，EF∥AB，AE∥MN，BF∥MN，由图中字母标出的 互相平行的直线共有( ) A．4组； B．5组；C．6组；D．7组
12．如图所示，直线AB，CD是一条河的两岸，并且AB∥CD，点E为直线AB，CD外一点，现想过点E作河岸CD的平行线，只需过点E作_____的平行线即可，其理由是________________________________　　
平行于同一条直线的两条直线平行．
13．在同一平面内，一条直线和两条平行线中的一条直线相交，那么这条直线与平行线中的另一条直线必__________。
14．观察下图所示的长方体，回答下列问题．(1)用符号表示两棱的位置关系： A1B1______AB，AA1_______AB，A1D1_______C1D1，AD____BC；(2)AB与B1C1所在的直线不相交，它们_____平行线(填“是”或“不是”)． 由此可知，在_________内，两条不相交的直线才是平行线．
15．在同一平面内，有三条直线a，b，c，它们之间有哪几种可能的位置关系？画图说明．
解：有四种可能的位置关系，如下图：
16．如图所示，在∠AOB内有一点P.(1)过P画l1∥OA；(2)过P画l2∥OB；(3)用量角器量一量l1与l2相交的角与∠O的大小有怎样的关系．
解：(1)(2)如图所示．(3)l1与l2的夹角有两个：∠1，∠2.因为∠1＝∠O，∠2＋∠O＝180°，所以l1与l2的夹角与∠O相等或互补．
17．如图所示，取一张长方形的硬纸板ABCD，将硬纸板ABCD对折使CD与AB重合，EF为折痕．把长方形ABFE平放在桌面上，另一个面CDEF无论怎么改变位置总有CD∥AB存在，你知道为什么吗？
解：∵AB∥EF，CD∥EF， ∴CD∥AB.
18．利用直尺画图：(1)利用图1中的网格，过P点画直线AB的平行线和垂线；(2)在图2的网格中画一个四边形，满足：①两组对边互相平行；②任意两个顶点都不在一条网格线上；③四个顶点都在格点上．
解：(1)CD∥AB，PQ⊥AB.(2)四边形ABCD是符合条件的四边形．
1.准确识别同位角、内错角、同旁内角是判 断两条直线平行的前提条件；2.垂直于同一条直线的两条直线平行.
烈火试真金，逆境试强者