2025年中考数学一轮复习学案：4.5 多边形与平行四边形 （学生版+教师版）

这是一份2025年中考数学一轮复习学案：4.5 多边形与平行四边形 （学生版+教师版），文件包含2025年中考数学一轮复习学案45多边形与平行四边形教师版docx、2025年中考数学一轮复习学案45多边形与平行四边形学生版docx等2份学案配套教学资源，其中学案共52页， 欢迎下载使用。
4.5 多边形与平行四边形
☆☆☆ 代表必考点，☆☆代表常考点，☆星表示选考点。


夯实基础
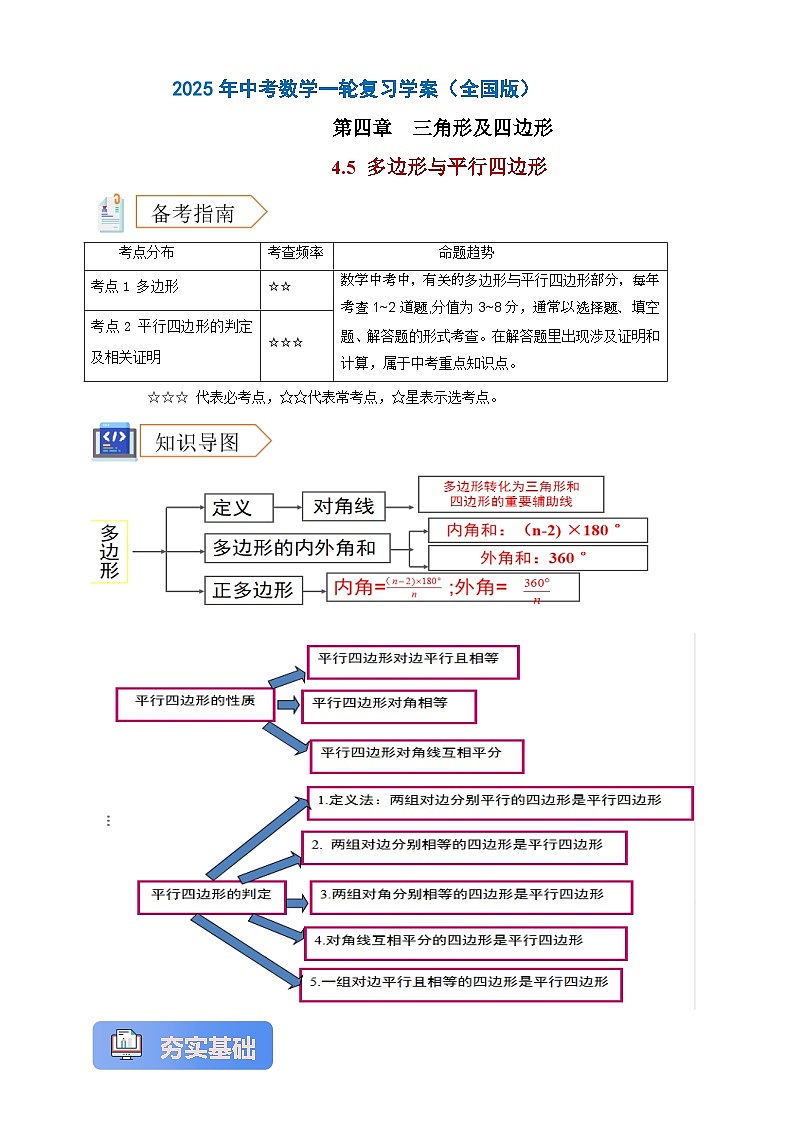
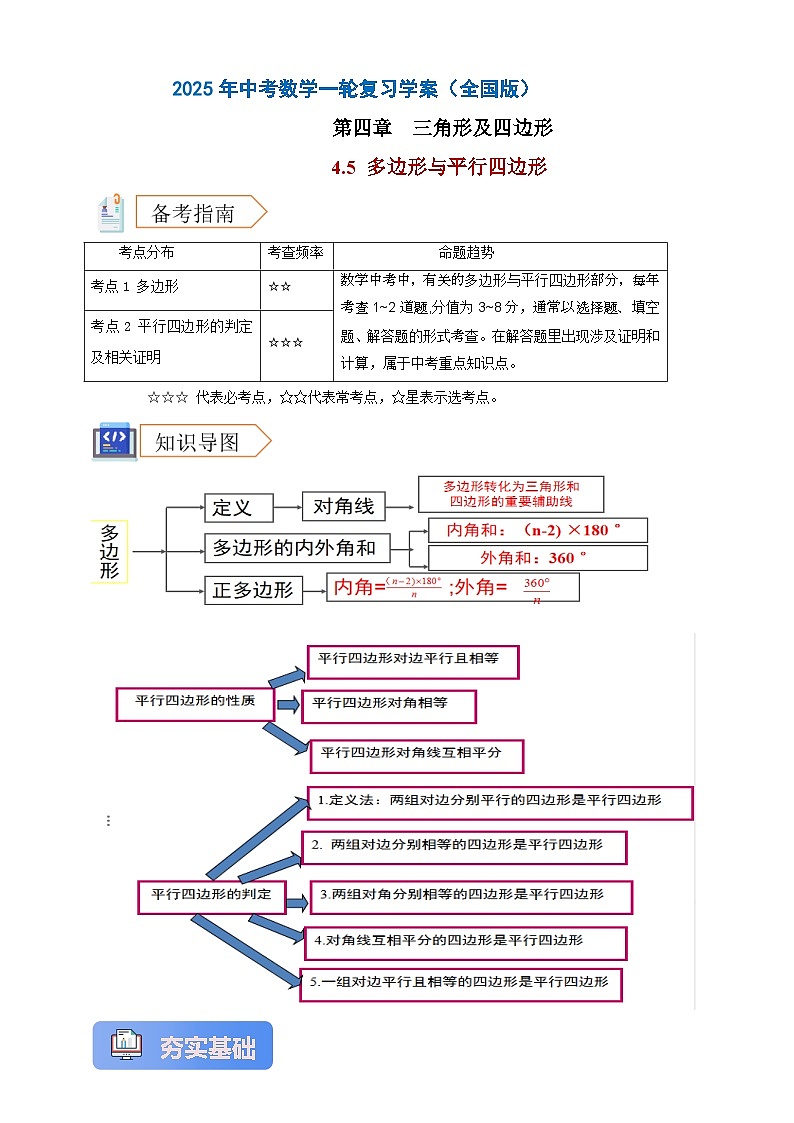
考点1. 多边形
1．多边形：在平面内，由一些线段首尾顺次相接组成的图形叫做多边形。
2．多边形的内角：多边形相邻两边组成的角叫做它的内角。
3．多边形的外角：多边形的一边与它的邻边的延长线组成的角叫多边形的外角。
4．多边形的对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的对角线。
5．正多边形：在平面内，各个角都相等，各条边都相等的多边形叫做正多边形。
6．多边形内角和公式：n边形的内角和等于（n-2）·180°
7．多边形的外角和：多边形的内角和为360°。
8.多边形对角线的条数：
（1）从n边形的一个顶点出发可以引（n-3）条对角线，把多边形分成（n-2）个三角形。
（2）n边形共有条对角线。
考点2. 平行四边形的判定及相关证明
1.平行四边形定义
有两组对边分别平行的四边形叫做平行四边形。平行四边形用符号“□ABCD”表示，读作“平行四边形ABCD”。
2.平行四边形的性质
（1）平行四边形的对边平行且相等；
（2）平行四边形的对角相等；
（3）平行四边形的对角线互相平分。
3.平行四边形的判定
（1）两组对边分别平行的四边形是平行四边形；
（2）两组对边分别相等的四边形是平行四边形；
（3）一组对边平行且相等的四边形是平行四边形；
（4）对角线互相平分的四边形是平行四边形；
（5）两组对角分别相等的四边形是平行四边形。
4.平行四边形的面积：S平行四边形=底边长×高=ah
5. 三角形中位线问题
1．三角形中位线的定义：连接三角形两边中点的线段叫做三角形的中位线。
2．三角形中位线定理：三角形的中位线平行于第三边，并且等于它的一半。
3.对三角形中位线的深刻理解
（1）三角形有三条中位线，每一条与第三边都有相应的位置关系与数量关系.
（2）三角形的三条中位线把原三角形分成可全等的4个小三角形.因而每个小三角形的周长为原三角形周长的，每个小三角形的面积为原三角形面积的.
（3）三角形的中位线不同于三角形的中线.
【易错点提示】
易错点1. 截角问题中忽视多种情况而致错
分析指导：截去一个角的方法不止一种，要按照截线经过的顶点的个数进行分类讨论：（1）不经过顶点；（2）经过一个顶点；（3）经过两个顶点.
易错点2. 无图的题目中因没有分类讨论而出现漏解
分析指导：对于题目中没有给出图形但需要画图形解答的题目，要考虑周到，画出符合条件的所有图形，以免漏解.
考点1. 多边形
【例题1】 （2024甘肃临夏）“香渡栏干屈曲，红妆映、薄绮疏棂．”图1窗棂的外边框为正六边形（如图2），则该正六边形的每个内角为______．

【答案】120
【解析】本题考查多边形内角和，正多边形的性质．掌握n边形内角和为和正多边形的每个内角都相等是解题关键．根据多边形内角和公式求出正六边形的内角和为，再除以6即可．
【详解】∵正六边形的内角和为，
∴正六边形的每个内角为．
【变式练1】（2024黑龙江龙东一模）已知一个多边形内角和是外角和的4倍，则这个多边形是（ ）
A. 八边形 B. 九边形 C. 十边形 D. 十二边形
【答案】C
【解析】设这个多边形的边数为n，然后根据内角和与外角和公式列方程求解即可.
设这个多边形的边数为n，
则（n－2）×180°＝4×360°，
解得：n＝10.
【点睛】本题主要考查多边形的内角和定理及多边形的外角和定理，熟练掌握多边形内角和定理是解答本题的关键.n变形的内角和为：(n-2) ×180°， n变形的外角和为：360°；然后根据等量关系列出方程求解．
【变式练2】 （2024上海一模）如果一个正多边形的中心角是，那么这个正多边形的边数为________．
【答案】18
【解析】根据正n边形的中心角的度数为进行计算即可得到答案．
根据正n边形的中心角的度数为，
则，
故这个正多边形的边数为18．
【点睛】本题考查的是正多边形内角和中心角的知识，掌握中心角的计算公式是解题的关键．
【变式练3】（2024湖南长沙一模）若一个多边形的内角和的比它的外角和多90°，那么这个多
边形的边数是多少？
【答案】12
【解析】设这个多边形的边数是n，
由题意得：（n﹣2）×180°﹣360°＝90°，
∴n＝12，
答：这个多边形的边数是12．
考点2. 平行四边形的判定及相关证明
【例题2】 （2024广西）如图，两张宽度均为的纸条交叉叠放在一起，交叉形成的锐角为，则重合部分构成的四边形的周长为______．
【答案】
【解析】本题考查了平行四边形的判定，菱形的判定和性质，菱形的周长，过点作于，于，由题意易得四边形是平行四边形，进而由平行四边形的面积可得，即可得到四边形是菱形，再解可得，即可求解，得出四边形是菱形是解题的关键．
【详解】过点作于，于，则，
∵两张纸条的对边平行，
∴，，
∴四边形是平行四边形，
又∵两张纸条的宽度相等，∴，
∵，∴，
∴四边形是菱形，
在中，，，
∴，
∴四边形的周长为
【变式练1】（2024郑州一模）如图，在四边形ABCD中，对角线AC和BD相交于点O，下列条件不能判断四边形ABCD是平行四边形的是（ ）
A．AB∥DC，AD∥BCB．AB＝DC，AD＝BC
C．AB∥DC，AD＝BCD．OA＝OC，OB＝OD
【答案】C
【解析】∵AB∥DC，AD∥BC，
∴四边形ABCD是平行四边形，故选项A中条件可以判定四边形ABCD是平行四边形；
∵AB＝DC，AD＝BC，
∴四边形ABCD是平行四边形，故选项B中条件可以判定四边形ABCD是平行四边形；
∵AB∥DC，AD＝BC，则无法判断四边形ABCD是平行四边形，故选项C中的条件，不能判断四边形ABCD是平行四边形；
∵OA＝OC，OB＝OD，
∴四边形ABCD是平行四边形，故选项D中条件可以判定四边形ABCD是平行四边形；
【变式练2】（2024福州一模）如图，在□ABCD中，BE⊥AB交对角线AC于点E，若∠1=20°，则∠2的度数是_______.
【答案】110°
【解析】本题考查了平行四边形的性质和和三角形外角的性质求角的大小，解题的关键是熟练运用平行四边形性质或三角形外角的有关知识．思路：首先利用平行四边形的性质求出∠BAE的度数，再由∠2是△ABE的外角求出∠2的大小.
∵四边形ABCD是平行四边形
∴AB∥CD，
∴∠BAE=∠1=20°
∵BE⊥AB
∴∠ABE=90°
∵∠2是△ABE的外角
∴∠2=∠ABE+∠BAE=90°+20°=110 ，故答案为110°.
【变式练3】（2024杭州一模）如图，□ABCD的对角线AC、BD相交于点O，EF过点O与AB、CD分别相交于点E、F.求证：OE＝OF.
【答案】见解析。
【解析】根据平行四边形的性质得出OD＝OB，DC∥AB，推出∠FDO＝∠EBO，证出△DFO≌△BEO即可．
证明：∵四边形ABCD是平行四边形，
∴OD＝OB，DC∥AB，∴∠FDO＝∠EBO.
在△DFO和△BEO中，eq \b\lc\{(\a\vs4\al\c1(∠FDO＝∠EBO，,OD＝OB，,∠FOD＝∠EOB，))
∴△DFO≌△BEO(ASA)，∴OE＝OF.
方法总结：利用平行四边形的性质解决线段的问题时，要注意运用平行四边形的对边相等，对角线互相平分的性质．
【变式练4】（中位线问题）如图，菱形ABCD周长为20，对角线AC、BD相交于点O，E是CD的中点，则OE的长是（ ）
A．2.5B．3C．4D．5
【答案】A
【解析】∵四边形ABCD为菱形，
∴CD＝BC QUOTE =204= =204=5，且O为BD的中点，
∵E为CD的中点，
∴OE为△BCD的中位线，
∴OE QUOTE =12 =12CB＝2.5
考点1. 多边形
1. （2024四川乐山）下列多边形中，内角和最小的是（ ）
A. B. C. D.
【答案】A
【解析】边数为n的多边形的内角和，分别求出三角形，四边形，五边形，六边形的内角和，即可得到．
三角形的内角和等于
四边形的内角和等于
五边形的内角和等于
六边形的内角和等于
所以三角形的内角和最小 故选：A．
【点睛】本题考查了多边形的内角和，能熟记边数为n的多边形的内角和是解此题的关键．
2. （2024云南省）一个七边形的内角和等于（ ）
A. B. C. D.
【答案】B
【解析】本题考查多边形的内角和，根据边形的内角和为求解，即可解题．
一个七边形的内角和等于，故选：B．
3. （2024重庆市A）如果一个多边形的每一个外角都是，那么这个多边形的边数为______．
【答案】9
【解析】本题考查了多边形的外角和定理，用外角和除以即可求解，掌握多边形的外角和等于是解题的关键．
，
∴这个多边形的边数是．
4. （2024河北省）直线l与正六边形的边分别相交于点M，N，如图所示，则（ ）
A. B. C. D.
【答案】B
【解析】本题考查了多边形的内角和，正多边形的每个内角，邻补角，熟练掌握知识点是解决本题的关键．
先求出正六边形的每个内角为，再根据六边形的内角和为即可求解的度数，最后根据邻补角的意义即可求解．
【详解】解：正六边形每个内角为：，
而六边形的内角和也为，
∴，
∴，
∵，
∴，故选：B．
5. （2024内蒙古赤峰）如图，是正边形纸片的一部分，其中是正边形两条边的一部分，若所在的直线相交形成的锐角为，则的值是（ ）
A. B. C. D.
【答案】B
【解析】本题考查了正多边形，求出正多边形的每个外角度数，再用外角和除以外角度数即可求解，掌握正多边形的性质是解题的关键．
【详解】如图，直线相交于点，则，
∵正多边形的每个内角相等，
∴正多边形的每个外角也相等，
∴，
∴，
故选：．
6. （2024山东枣庄）如图，已知，，是正边形的三条边，在同一平面内，以为边在该正边形的外部作正方形．若，则的值为（ ）
A. 12B. 10C. 8D. 6
【答案】A
【解析】本题考查的是正多边形的性质，正多边形的外角和，先求解正多边形的1个内角度数，得到正多边形的1个外角度数，再结合外角和可得答案.
【详解】∵正方形，
∴，
∵，
∴，
∴正边形的一个外角为，
∴的值为；故选A
7. （2024内蒙古包头）已知一个n边形的内角和是，则________．
【答案】7
【解析】本题考查根据多边形的内角和计算公式求多边形的边数，多边形的内角和可以表示成，依此列方程可求解．
根据题意，得，
解得
8. （2024山东威海）如图，在正六边形中，，，垂足为点I．若，则________．
【答案】##50度
【解析】本题考查了正六边形的内角和、平行线的性质及三角形内角和定理，先求出正六边形的每个内角为，即，则可求得的度数，根据平行线的性质可求得的度数，进而可求出的度数，再根据三角形内角和定理即可求出的度数．
∵正六边形的内角和，
每个内角为：，
，
，
，
，
，
，
，
，
，
．
考点2.平行四边形的判定及相关证明
1. （2024贵州省）如图，平行四边形ABCD的对角线与相交于点O，则下列结论一定正确的是（ ）
A.B. C. D.
【答案】B
【解析】本题主要考查平行四边形的性质，掌握平行四边形的对边平行且相等，对角线互相平分是解题的关键．
∵是平行四边形，
∴，故选B．
2. （2024河南省）如图，在中，对角线，相交于点O，点E为的中点，交于点F．若，则的长为（ ）
A. B. 1C. D. 2
【答案】B
【解析】本题考查了相似三角形的判定与性质，平行四边形的性质等知识，利用平行四边形的性质、线段中点定义可得出，证明，利用相似三角形的性质求解即可．
【详解】∵四边形是平行四边形，
∴，
∵点E为的中点，
∴，
∵，
∴，
∴，即，
∴，故选：B．
3. （2024四川广安）如图，在中，点，分别是，的中点，若，，则的度数为（ ）
A. B. C. D.
【答案】D
【解析】本题考查了三角形中位线定理、平行线性质定理，三角形的内角和定理，熟记性质并准确识图是解题的关键．先证明，可得，再利用三角形的内角和定理可得答案.
【详解】∵点，分别是，的中点，
∴，
∵，
∴，
∵，
∴，故选D
4. （2024湖南长沙）如图，在中，点D，E分别是的中点，连接．若，则的长为______．
【答案】24
【解析】本题主要考查三角形中位线定理，熟知三角形的中位线平行于第三边且等于第三边的一半是解题的关键．
∵D，E分别是，的中点，
∴是的中点，
∴．
5. （2024重庆市A）如图，在中，延长至点，使，过点作，且，连接交于点．若，，则______．
【答案】
【解析】先根据平行线分线段成比例证，进而得，，再证明，得，从而即可得解．
【详解】∵，过点作，，，
∴，，
∴，
∴，
∴，
∵，
∴，，
∵，
∴，
∵，，
∴，
∴，
∴，
∴，故答案为：，
【点睛】本题主要考查了平行线的性质，三角形的中位线定理，平行线分线段成比例以及全等三角形的判定及性质，熟练掌握三角形的中位线定理，平行线分线段成比例以及全等三角形的判定及性质是解题的关键．
6. （2024河北省）下面是嘉嘉作业本上的一道习题及解答过程：
若以上解答过程正确，①，②应分别为（ ）
A. ，B. ，
C. ，D. ，
【答案】D
【解析】本题考查平行四边形的判定，全等三角形的判定与性质，根据等边对等角得，根据三角形外角的性质及角平分线的定义可得，证明，得到，再结合中点的定义得出，即可得证．解题的关键是掌握：对角线互相平分的四边形是平行四边形．
【详解】证明：∵，∴．
∵，，，
∴①．
又∵，，
∴（②）．
∴．∴四边形是平行四边形．故选：D．
7. （2024广州）如图，平行四边形ABCD中，，点在的延长线上，，若平分，则______．
【答案】5
【解析】本题考查了平行四边形的性质，等腰三角形的判定和性质，掌握平行四边形的性质是解题关键．由平行四边形的性质可知，，，进而得出，再由等角对等边的性质，得到，即可求出的长．
【详解】在平行四边形ABCD中，，
，，
，
平分，
，
，
，
．
8. （2024武汉市）如图，在平行四边形ABCD中，点，分别在边，上，．
（1）求证：；
（2）连接．请添加一个与线段相关的条件，使四边形是平行四边形．（不需要说明理由）
【答案】（1）见解析 （2）添加（答案不唯一）
【解析】本题考查了平行四边形的性质与判定，全等三角形的判定；
（1）根据平行四边形的性质得出，，结合已知条件可得，即可证明；
（2）添加，依据一组对边平行且相等的四边形是平行四边形，即可求解．
【小问1详解】
证明：∵四边形是平行四边形，
∴，，，
∵，
∴即，
在与中，
，
∴；
【小问2详解】
添加（答案不唯一）
如图所示，连接．
∵四边形是平行四边形，
∴，即，
当时，四边形是平行四边形．
9. （2024湖北省）已知：如图，E，F为□ABCD对角线AC上的两点，且AE=CF，连接BE，DF，求证：BE=DF．
【答案】证明见解析．
【解析】利用SAS证明△AEB≌△CFD，再根据全等三角形的对应边相等即可得．
∵四边形ABCD是平行四边形，
∴AB//DC，AB=DC，
∴∠BAE=∠DCF，
在△AEB和△CFD中，
，
∴△AEB≌△CFD（SAS），
∴BE=DF．
【点睛】本题考查了平行四边形的性质以及全等三角形的判定与性质，熟练掌握相关的性质是解题的关键．
10. （2024湖南省）如图，在四边形中，，点E在边上， ．请从“①；②，”这两组条件中任选一组作为已知条件，填在横线上（填序号），再解决下列问题：
（1）求证：四边形为平行四边形；
（2）若，，，求线段的长．
【答案】（1）①或②，证明见解析； （2）6
【解析】题目主要考查平行四边形的判定和性质，勾股定理解三角形，理解题意，熟练掌握平行四边形的判定和性质是解题关键．
（1）选择①或②，利用平行四边形的判定证明即可；
（2）根据平行四边形的性质得出，再由勾股定理即可求解．
【小问1详解】
解：选择①，
证明：∵，
∴，
∵，
∴四边形为平行四边形；
选择②，
证明：∵，，
∴，
∵，
∴四边形为平行四边形；
【小问2详解】
解：由（1）得，
∵，，
∴．
11.（2024黑龙江大庆） 如图，平行四边形中，、分别是，的平分线，且E、F分别在边，上．
（1）求证：四边形是平行四边形；
（2）若，，求的面积．
【答案】（1）见解析 （2）．
【解析】【分析】（1）由平行四边形的性质得到，，结合角平分线的条件得到，由得到，，根据平行线的判定得到，根据平行四边形的判定即可得到是平行四边形；
（2）求得是等边三角形，得到，，证明，求得，作于点，在中，求得，据此求解即可．
【小问1详解】
证明：∵四边形是平行四边形，
∴，，
∵分别是、的平分线，
∴，，
∴，
∵，
∴，
∴，
∴，
∴四边形是平行四边形；
【小问2详解】
解：由（1）得，，
∴，
∵，
∴是等边三角形，
∴，
∵，
∴，，
∵，
∴，
∴，
∴，
作于点，
在中，，，
∴，
∴．
【点睛】本题考查了解直角三角形，相似三角形的判定和性质，勾股定理，平行四边形的判定和性质，等边三角形的判定和性质．正确引出辅助线解决问题是解题的关键．
12. （2024深圳）垂中平行四边形的定义如下：在平行四边形中，过一个顶点作关于不相邻的两个顶点的对角线的垂线交平行四边形的一条边，若交点是这条边的中点，则该平行四边形是“垂中平行四边形”．
（1）如图1所示，四边形为“垂中平行四边形”，，，则________；________；
（2）如图2，若四边形为“垂中平行四边形”，且，猜想与的关系，并说明理由；
（3）①如图3所示，在中，，，交于点，请画出以为边的垂中平行四边形，要求：点在垂中平行四边形的一条边上（温馨提示：不限作图工具）；
②若关于直线对称得到，连接，作射线交①中所画平行四边形的边于点，连接，请直接写出的值．
【答案】（1），
（2），理由见解析
（3）①见解析；②或．
【解析】【分析】（1）根据题意可推出，得到，从而推出，再根据勾股定理可求得，再求得；
（2）根据题意可推出，得到，设，则，，再利用勾股定理得到，从而推出、，即可求得答案；
（3）①分情况讨论，第一种情况，作的平行线，使，连接，延长交于点；第二种情况，作的平分线，取交的平分线于点，延长交的延长线于点，在射线上取，连接；第三种情况，作，交的延长线于点，连接，作的垂直平分线；
在延长线上取点F，使，连接；
②根据①中的三种情况讨论：
第一种情况，根据题意可证得是等腰三角形，作，则，可推出，从而推出，计算可得，最后利用勾股定理即可求得；
第二种情况，延长、交于点，同理可得是等腰三角形，连接，可由，结合三线合一推出，从而推出，同第一种情况即可求得；
第三种情况无交点，不符合题意．
【小问1详解】
解：，为的中点，，，，
，，
，即，解得，
，
；
故答案为：1；；
【小问2详解】
解：，理由如下：
根据题意，在垂中四边形中，，且为的中点，
，；
又，
，
；
设，则，
，
，
，，
，
，
，
；
【小问3详解】
解：①第一种情况：
作的平行线，使，连接，
则四边形为平行四边形；
延长交于点，
，
，
，
，，
，即，
为的中点；
故如图1所示，四边形即为所求的垂中平行四边形：

第二种情况：
作的平分线，取交的平分线于点，延长交的延长线于点，在射线上取，连接，
故为的中点；
同理可证明：，
则，
则四边形是平行四边形；
故如图2所示，四边形即为所求的垂中平行四边形：
第三种情况：
作，交的延长线于点，连接，作的垂直平分线；
在延长线上取点F，使，连接，
则为的中点，
同理可证明，从而，
故四边形是平行四边形；
故如图3所示，四边形即为所求的垂中平行四边形：
②若按照图1作图，
由题意可知，，
四边形是平行四边形，
，
，
是等腰三角形；
过P作于H，则，
，，
，，
，
；
,，
，
，即
∴
若按照图2作图，
延长、交于点，
同理可得：是等腰三角形，
连接，
，
，
，
，
；
同理，，
，，，
，即，
，
若按照图3作图，则：没有交点，不存在PE（不符合题意）
故答案为：或．
【点睛】本题考查了垂中平行四边形的定义，平行四边形的性质与判定，相似三角形的判定与性质，勾股定理，尺规作图，等腰三角形的判定与性质等，熟练掌握以上知识点，读懂题意并作出合适的辅助线是解题的关键．
考点1. 多边形
1.一个多边形的内角和为900°，则这个多边形是（ ）
A. 七边形B. 八边形C. 九边形D. 十边形
【答案】A
【解析】根据n边形的内角和是（n﹣2）•180°，列出方程即可求解．
根据n边形的内角和公式，得
（n﹣2）•180°=900°，
解得n=7，
∴这个多边形的边数是7，故选：A．
【点睛】本题考查了多边形的内角和，解题的关键是熟记内角和公式并列出方程．
2．一个10边形的内角和等于（ ）
A．1800°B．1660°C．1440°D．1200°
【答案】C
【解析】根据多边形的内角和等于（n﹣2）•180°即可得解．
根据多边形内角和公式得，10边形的内角和等于：
（10﹣2）×180°＝8×180°＝1440°．
【点评】此题考查了多边形的内角与外角，熟记多边形的内角和公式是解题的关键．
3．如图，正五边形ABCDE中，∠CAD的度数为（ ）
A．72°B．45°C．36°D．35°
【答案】C
【解析】首先可根据五边形内角和公式求出每个内角的度数，然后求出∠CAB和∠DAE，即可求出∠CAD．
根据正多边形内角和公式可得，
正五边形ABCDE的内角和＝180°×（5﹣2）＝540°，
则∠BAE＝∠B＝∠E＝＝108°，
根据正五边形的性质，△ABC≌△AED，
∴∠CAB＝∠DAE＝（180°﹣108°）＝36°，
∴∠CAD＝108°﹣36°﹣36°＝36°.
4．若正多边形的一个外角是45°，则该正多边形的内角和为（ ）
A．540°B．720°C．900°D．1080°
【答案】D
【解析】先根据多边形的外角和定理求出多边形的边数，再根据多边形的内角和公式求出这个正多边形的内角和．
正多边形的边数为：360°÷45°＝8，
∴这个多边形是正八边形，
∴该多边形的内角和为（8﹣2）×180°＝1080°．
5. （2022四川眉山）一个多边形外角和是内角和的，则这个多边形的边数为________．
【答案】11
【解析】多边形的内角和定理为，多边形的外角和为360°，根据题意列出方程求出n的值．
根据题意可得：，
解得： ．
【点睛】本题主要考查的是多边形的内角和公式以及外角和定理，属于基础题型．记忆理解并应用这两个公式是解题的关键．
6. 如图，正六边形和正五边形内接于，且有公共顶点A，则的度数为______度．
【答案】12
【解析】连接AO，求出正六边形和正五边形的中心角即可作答．
连接AO，如图，
∵多边形ABCDEF是正六边形，
∴∠AOB=360°÷6=60°，
∵多边形AHIJK是正五边形，
∴∠AOH=360°÷5=72°，
∴∠BOH=∠AOH-∠AOB=72°-60°=12°．
【点睛】本题考查了正多边形的中心角的知识，掌握正多边形中心角的计算方法是解答本题的关键．
7．如图，一个正五边形和一个正六边形有一个公共顶点O，则∠1+∠2＝ ．
【答案】132°．
【解析】∵正五边形的每个内角度数＝180°﹣360°÷5＝108°，
正六边形的每个内角度数＝180°﹣360°÷6＝120°，
∴∠1+∠2+108°+120°＝360°，
∴∠1+∠2＝132°．
考点2.平行四边形的判定及相关证明
1．下列条件中，能判定四边形是平行四边形的是（ ）
A．对角线互相平分
B．对角线互相垂直
C．对角线相等
D．对角线互相垂直且相等
【答案】A
【解析】A、对角线互相平分的四边形是平行四边形．正确．
B、对角线互相垂直的四边形不一定是平行四边形．错误．
C、对角线相等的四边形不一定是平行四边形．错误．
D、对角线互相垂直且相等的四边形不一定是平行四边形．错误．
故选：A．
2. 如图，点O是□ABCD对角线的交点，EF过点O分别交AD，BC于点E，F，下列结论成立的
是（ ）
A．OE＝OFB．AE＝BFC．∠DOC＝∠OCDD．∠CFE＝∠DEF
【答案】A
【解析】证△AOE≌△COF（ASA），得OE＝OF，AE＝CF，∠CFE＝∠AEF，进而得出结论．
∵▱ABCD的对角线AC，BD交于点O，
∴AO＝CO，BO＝DO，AD∥BC，
∴∠EAO＝∠FCO，
在△AOE和△COF中，
，
∴△AOE≌△COF（ASA），
∴OE＝OF，AE＝CF，∠CFE＝∠AEF，
又∵∠DOC＝∠BOA，
∴选项A正确，选项B、C、D不正确．
3. 如图，在□ABCD中，AE平分∠BAD且交BC于点E，∠D＝58°，则∠AEC的大小是（ ）
A．61°B．109°C．119°D．122°
【答案】C
【解析】由平行四边形的性质可得∠BAD＝122°，∠B＝∠D＝58°，由角平分线的性质和外角性质可求解．
∵四边形ABCD是平行四边形，∠D＝58°，
∴∠BAD＝122°，∠B＝∠D＝58°，
∵AE平分∠BAD，
∴∠BAE＝61°，
∴∠AEC＝∠B+∠BAE＝119°．
4．如图，在▱ABCD中，∠ABC的平分线交AD于点E，∠BCD的平分线交AD于点F，若AB＝3，AD＝4，则EF的长是（ ）
A．1B．2C．2.5D．3
【答案】B
【解析】根据平行四边形的性质证明DF＝CD，AE＝AB，进而可得AF和ED的长，然后可得答案．
∵四边形ABCD是平行四边形，
∴AD∥CB，AB＝CD＝3，AD＝BC＝5，
∴∠DFC＝∠FCB，
又∵CF平分∠BCD，
∴∠DCF＝∠FCB，
∴∠DFC＝∠DCF，
∴DF＝DC＝3，
同理可证：AE＝AB＝3，
∵AD＝4，
∴AF＝5﹣4＝1，DE＝4﹣3＝1，
∴EF＝4﹣1﹣1＝2．
5．如图，在□ABCD中，AB＝13，AD＝5，AC⊥BC，则▱ABCD的面积为（ ）
A．30B．60C．65D．
【答案】B
【解析】根据平行四边形的性质以及勾股定理求出四边形ABCD的底边BC和其对角线AC的值，然后根据平行四边形的面积计算公式求解．
∵四边形ABCD为平行四边形，
∴BC＝AD＝5．
∵AC⊥BC，
∴△ACB是直角三角形．
∴AC＝＝＝12．
∴S▱ABCD＝BC•AC＝5×12＝60．
6．如图，在四边形ABCD中AB∥CD，若加上AD∥BC，则四边形ABCD为平行四边形．现在请你添加一个适当的条件： ，使得四边形AECF为平行四边形．（图中不再添加点和线）
【答案】BE＝DF．
【解析】添加的条件：BE＝DF．
证明：∵四边形ABCD为平行四边形
∴AB＝CD，∠ABE＝∠CDF
又∵BE＝DF
∴△ABE≌△CDF
∴AE＝CF，∠AEB＝∠CFD
∴∠AEF＝∠EFC
∴AE∥FC
∴四边形AECF为平行四边形．
故答案为：BE＝DF．
7．四边形ABCD是平行四边形，AB＝6，∠BAD的平分线交直线BC于点E，若CE＝2，则▱ABCD的周长为 ．
【答案】28．
【解析】由平行四边形的性质知BC∥AD，由平行线的性质即角平分线的定义可得∠BEA＝∠BAE，进而可求解BE的长，即可求得BC的长，再根据平行四边形的周长可求解．
如图：
∵四边形ABCD为平行四边形，
∴BC∥AD，
∴∠BEA＝∠EAD，
∵AE平分∠BAD，
∴∠BAE＝∠EAD，
∴∠BEA＝∠BAE，
∴BE＝AB，
∵AB＝6，
∴BE＝6，
∵CE＝2，
∴BC＝BE+CE＝6+2＝8，
∴平行四边形ABCD的周长为：2×（6+8）＝28，
8．如图，在□ABCD中，对角线AC，BD交于点O，AB⊥AC，AH⊥BD于点H，若AB＝2，BC＝2，则AH的长为 ．
【答案】．
【解析】在Rt△ABC和Rt△OAB中，分别利用勾股定理可求出BC和OB的长，又AH⊥OB，可利用等面积法求出AH的长．
如图，
∵AB⊥AC，AB＝2，BC＝2，
∴AC＝＝2，
在▱ABCD中，OA＝OC，OB＝OD，
∴OA＝OC＝，
在Rt△OAB中，
OB＝＝，
又AH⊥BD，
∴OB•AH＝OA•AB，即＝，
解得AH＝．
9．如图，在平行四边形ABCD中，BE平分∠ABC，CF⊥BE，连接AE，G是AB的中点，连接GF，若AE＝4，则GF＝_____．
【答案】2
【解析】根据平行四边形的性质结合角平分线的定义可求解∠CBE=∠BEC，即可得CB=CE，利用等腰三角形的性质得到BF=EF，进而可得GF是△ABE的中位线，根据三角形的中位线的性质可求解．
在平行四边形ABCD中，AB∥CD，∴∠ABE=∠BEC．
∵BE平分∠ABC，∴∠ABE=∠CBE，∴∠CBE=∠BEC，∴CB=CE．
∵CF⊥BE，∴BF=EF．∵G是AB的中点，∴GF是△ABE的中位线，∴GF=AE，
∵AE=4，∴GF=2．故答案为：2．
【点睛】本题主要考查了平行四边形的性质，等腰三角形的性质与判定，三角形中位线的性质，证明GF是△ABE的中位线是解题的关键．
10．如图，在△ABC中，M，N分别是AB和AC的中点，连接MN，点E是CN的中点，连接ME并延长，交BC的延长线于点D．若BC＝4，则CD的长为 ．
【答案】2
【解析】依据三角形中位线定理，即可得到MN=12BC＝2，MN∥BC，依据△MNE≌△DCE（AAS），即可得到CD＝MN＝2．
∵M，N分别是AB和AC的中点，
∴MN是△ABC的中位线，
∴MN=12BC＝2，MN∥BC，
∴∠NME＝∠D，∠MNE＝∠DCE，
∵点E是CN的中点，
∴NE＝CE，
∴△MNE≌△DCE（AAS），
∴CD＝MN＝2．
11. 证明：平行四边形的对边相等。平行四边形的对角相等。
【解析】已知：四边形ABCD是平行四边形.
求证:AD=BC,AB=CD,∠BAD=∠BCD,∠ABC=∠ADC.
证明：如图，连接AC.
∵四边形ABCD是平行四边形,
∴AD∥BC，AB ∥ CD,
∴∠1=∠2，∠3=∠4.
又∵AC是△ABC和△CDA的公共边，
∴ △ABC≌△CDA,
∴AD=BC，AB=CD，∠ABC=∠ADC.
∵∠BAD=∠1+∠4，∠BCD=∠2+∠3，
∴∠BAD=∠BCD.
不添加辅助线，利用平行线性质也能证明。
12. 如图，四边形ABCD中，AB∥DC，∠B＝55°，∠1＝85°，∠2＝40°.
(1)求∠D的度数；
(2)求证：四边形ABCD是平行四边形．
【答案】见解析。
【解析】(1)解：∵∠D＋∠2＋∠1＝180°，
∴∠D＝180°－∠2－∠1＝55°；
(2)证明：∵AB∥DC，
∴∠2＝∠CAB，
∴∠DAB＝∠1＋∠2＝125°.
∵∠DCB＋∠DAB＋∠D＋∠B＝360°，
∴∠DCB＝∠DAB＝125°.
又∵∠D＝∠B＝55°，
∴四边形ABCD是平行四边形．
13.如图，已知四边形ABCD是平行四边形，BE⊥AC于点E，DF⊥AC于点F.
(1)求证：△ABE≌△CDF；
(2)连接BF、DE，试判断四边形BFDE是什么样的四边形？写出你的结论并予以证明．
【答案】见解析
【解析】(1)根据“AAS”可证出△ABE≌△CDF；(2)首先根据△ABE≌△CDF得出AE＝FC，BE＝DF.再利用已知得出△ADE≌△CBF，进而得出DE＝BF，即可得出四边形BFDE是平行四边形．
（1）证明：∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD，∴∠BAC＝∠DCA.∵BE⊥AC于E，DF⊥AC于F，∴∠AEB＝∠DFC＝90°.在△ABE和△CDF中，
eq \b\lc\{(\a\vs4\al\c1(∠DFC＝∠BEA，,∠FCD＝∠EAB，,AB＝CD，))∴△ABE≌△CDF(AAS)；
（2）解：四边形BFDE是平行四边形．理由如下：∵△ABE≌△CDF，∴AE＝FC，BE＝DF.∵四边形ABCD是平行四边形，∴AD＝CB，AD∥CB，∴∠DAC＝∠BCA.在△ADE和△CBF中，
eq \b\lc\{(\a\vs4\al\c1(AD＝BC，,∠DAE＝∠BCF，,AE＝FC，))∴△ADE≌△CBF(SAS)，∴DE＝BF，∴四边形BFDE是平行四边形．
方法总结：熟练运用平行四边形的性质，可证明三角形全等，证明边相等，再利用两组对边分别相等可判定四边形是平行四边形．
14.如图，E为□ABCD中DC边的延长线上一点，且CE＝DC，连接AE，分别交BC、BD于点F、G，连接AC交BD于O，连接OF，判断AB与OF的位置关系和大小关系，并证明你的结论．
【答案】见解析。
【解析】本题可先证明△ABF≌△ECF，从而得出BF＝CF，这样就得出了OF是△ABC的中位线，从而利用中位线定理即可得出线段OF与线段AB的关系．
AB∥OF，AB＝2OF.证明如下：∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD，OA＝OC，∴∠BAF＝∠CEF，∠ABF＝∠ECF.∵CE＝DC，∴AB＝CE.在△ABF和△ECF中，
eq \b\lc\{(\a\vs4\al\c1(∠BAF＝∠CEF，,AB＝CE，,∠ABF＝∠ECF，))
∴△ABF≌△ECF(ASA)，∴BF＝CF.
∵OA＝OC，
∴OF是△ABC的中位线，∴AB∥OF，AB＝2OF.
方法总结：本题综合的知识点比较多，解答本题的关键是判断出OF是△ABC的中位线．
15．如图，点B、E、C、F在一条直线上，AB=DF，AC=DE，BE=FC．
（1）求证：△ABC≌△DFE；
（2）连接AF、BD，求证：四边形ABDF是平行四边形．
【答案】见解析
【解析】证明：（1）∵BE=FC，
∴BC=EF，
在△ABC和△DFE中，，
∴△ABC≌△DFE（SSS）；
（2）解：如图所示：
由（1）知△ABC≌△DFE，
∴∠ABC=∠DFE，∴AB∥DF，
∵AB=DF，
∴四边形ABDF是平行四边形．
【点评】本题考查了平行四边形的判定、全等三角形的判定与性质、平行线的判定；熟练掌握平行四边形的判定方法，证明三角形全等是解决问题的关键．
16. 如图，AB、CD相交于点O，AC∥DB，AO＝BO，E、F分别是OC、OD的中点．求证：
(1)△AOC≌△BOD；
(2)四边形AFBE是平行四边形．
证明：(1)∵AC∥BD，
∴∠C＝∠D.
又∵∠COA=∠DOB，AO＝BO ，
∴△AOC≌△BOD(AAS)；
(2)∵△AOC≌△BOD，
∴CO＝DO.
∵E、F分别是OC、OD的中点，
∴EO＝FO.
又∵AO＝BO，
∴四边形AFBE是平行四边形．
17.如图，△ABC是等腰直角三角形，∠ACB=90°，分别以AB，AC为直角边向外作等腰直角△ABD和等腰直角△ACE，G为BD的中点，连接CG，BE，CD，BE与CD交于点F．
（1）判断四边形ACGD的形状，并说明理由．
（2）求证：BE=CD，BE⊥CD．
【答案】看解析。
【解析】（1）∵△ABC是等腰直角三角形，∠ACB=90°，
∴AB=BC，
∵△ABD和△ACE均为等腰直角三角形，
∴BD==BC=2BC，
∵G为BD的中点，
∴BG=BD=BC，
∴△CBG为等腰直角三角形，∴∠CGB=45°，
∵∠ADB=45°，
AD∥CG，
∵∠ABD=45°，∠ABC=45°∴∠CBD=90°，
∵∠ACB=90°，
∴∠CBD+∠ACB=180°，∴AC∥BD，∴四边形ACGD为平行四边形；
（2）证明：∵∠EAB=∠EAC+∠CAB=90°+45°=135°，
∠CAD=∠DAB+∠BAC=90°+45°=135°，∴∠EAB=∠CAD，
在△DAC与△BAE中，
，
∴△DAC≌△BAE，∴BE=CD；
∵∠EAC=∠BCA=90°，EA=AC=BC，
∴四边形ABCE为平行四边形，∴CE=AB=AD，
在△BCE与△CAD中，
，
∴△BCE≌△CAD，∴∠CBE=∠ACD，
∵∠ACD+∠BCD=90°，∴∠CBE+∠BCD=90°，∴∠CFB=90°，即BE⊥CD．
考点分布
考查频率
命题趋势
考点1 多边形
☆☆
数学中考中，有关的多边形与平行四边形部分，每年考查1~2道题,分值为3~8分，通常以选择题、填空题、解答题的形式考查。在解答题里出现涉及证明和计算，属于中考重点知识点。
考点2 平行四边形的判定及相关证明
☆☆☆
已知：如图，中，，平分的外角，点是的中点，连接并延长交于点，连接．
求证：四边形是平行四边形．
证明：∵，∴．
∵，，，
∴①______．
又∵，，
∴（②______）．
∴．∴四边形是平行四边形．