中考数学三轮考前专项冲刺练习：相似三角形（含答案解析）

这是一份中考数学三轮考前专项冲刺练习：相似三角形（含答案解析），共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（2022·浙江丽水）如图，五线谱是由等距离、等长度的五条平行横线组成的，同一条直线上的三个点A，B，C都在横线上．若线段，则线段的长是（ ）
A．B．1C．D．2
2．（2021·浙江绍兴市·中考真题）如图，中，，，点D是边BC的中点，以AD为底边在其右侧作等腰三角形ADE，使，连结CE，则的值为（ ）
A．B．C．D．
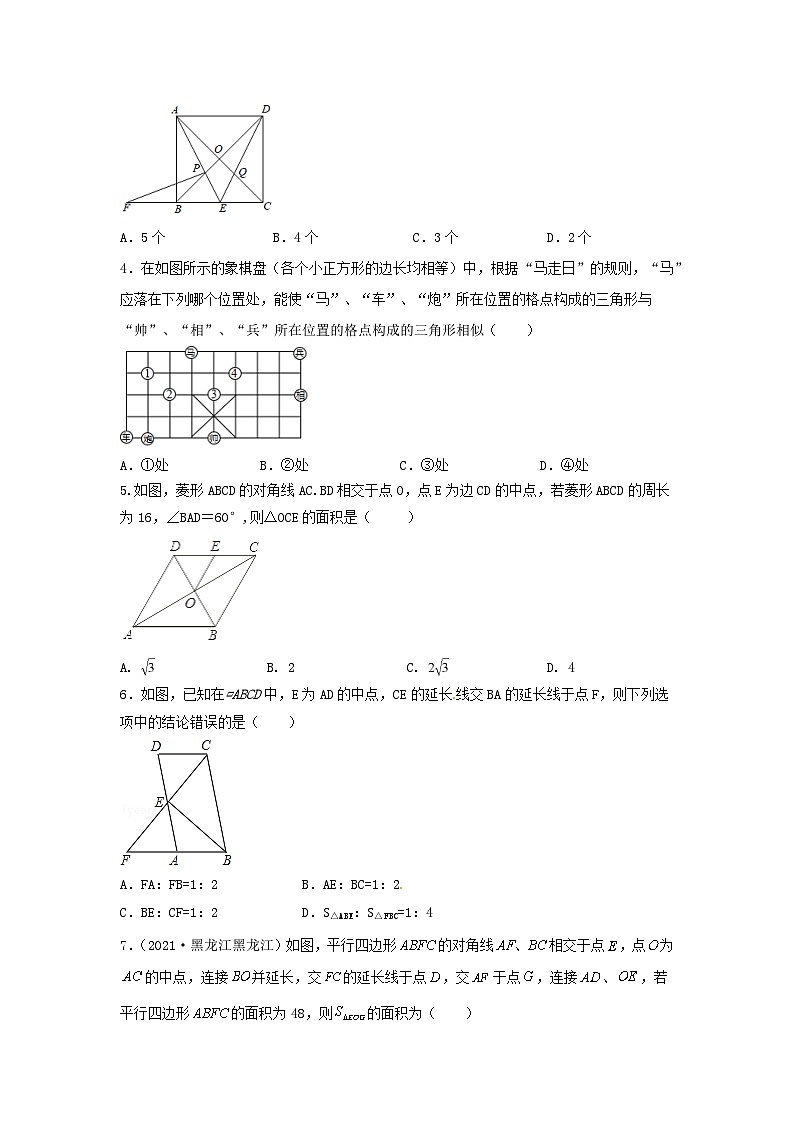
3.如图，在正方形ABCD中，点E是边BC的中点，连接AE、DE，分别交BD、AC于点P、Q，过点P作PF⊥AE交CB的延长线于F，下列结论：
①∠AED+∠EAC+∠EDB＝90°，
②AP＝FP，
③AE=102AO，
④若四边形OPEQ的面积为4，则该正方形ABCD的面积为36，
⑤CE•EF＝EQ•DE．
其中正确的结论有（ ）
A．5个B．4个C．3个D．2个
4．在如图所示的象棋盘（各个小正方形的边长均相等）中，根据“马走日”的规则，“马”应落在下列哪个位置处，能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、“兵”所在位置的格点构成的三角形相似（ ）
A．①处B．②处C．③处D．④处
5.如图，菱形ABCD的对角线AC.BD相交于点O，点E为边CD的中点，若菱形ABCD的周长为16，∠BAD＝60°,则△OCE的面积是（ ）
A. B. 2 C. D. 4
6．如图，已知在▱ABCD中，E为AD的中点，CE的延长线交BA的延长线于点F，则下列选项中的结论错误的是（ ）
A．FA：FB=1：2 B．AE：BC=1：2
C．BE：CF=1：2 D．S△ABE：S△FBC=1：4
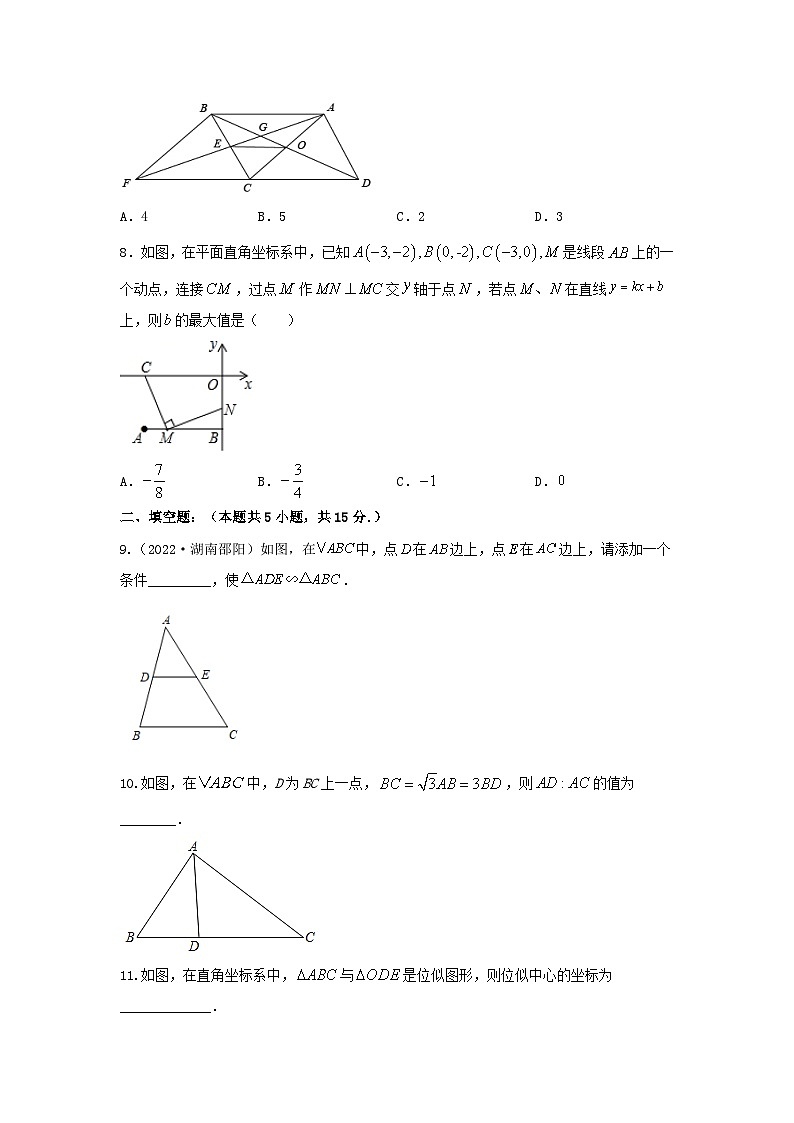
7．（2021·黑龙江黑龙江）如图，平行四边形的对角线相交于点，点为的中点，连接并延长，交的延长线于点，交于点，连接、，若平行四边形的面积为48，则的面积为（ ）
A．4B．5C．2D．3
8．如图，在平面直角坐标系中，已知是线段上的一个动点，连接，过点作交轴于点，若点在直线上，则的最大值是（ ）
A．B．C．D．
二、填空题：（本题共5小题，共15分．）
9.（2022·湖南邵阳）如图，在中，点在边上，点在边上，请添加一个条件_________，使．
10.如图，在中，D为BC上一点，，则的值为________．
11.如图，在直角坐标系中，与是位似图形，则位似中心的坐标为_____________．
12.（2020·辽宁锦州）如图，在中，D是中点，，若的周长为6，则的周长为______．

13.如图，在中，点E是的中点，，的延长线交于点F．若的面积为1，则四边形的面积为________．
三、解答题：（本题共3题，共45分．）
14．（2021·湖南益阳）如图，在等腰锐角三角形中，，过点B作于D，延长交的外接圆于点E，过点A作于F，的延长线交于点G．
（1）判断是否平分，并说明理由；
（2）求证：①；②．
15．如图，△ADE由△ABC绕点A按逆时针方向旋转90°得到，且点B的对应点D恰好落在BC的延长线上，AD，EC相交于点P．
（1）求∠BDE的度数；
（2）F是EC延长线上的点，且∠CDF＝∠DAC．
①判断DF和PF的数量关系，并证明；
②求证：EPPF=PCCF．
16．在矩形ABCD中，E为上的一点，把沿AE翻折，使点D恰好落在BC边上的点F．（1）求证：（2）若，求EC的长；
（3）若，记，求的值．
参考答案：
1.C 2.D 3.B 4.B 5.A 6.C 7.C 8.A
9.∠ADE=∠B（答案不唯一）．
10.．
11.
12.12
13.3
14.解：（1）平分，理由如下：
，
，
由圆周角定理得：，
，
由圆内接四边形的性质得：，
，
，
，
平分；
（2）①平分，，，
，
在和中，，
，
；
②在和，，
，
，
由圆内接四边形的性质得：，
，
，
，
，
在和中，，
，
，
，，
，
，
即．
15.（1）∵△ADE由△ABC绕点A按逆时针方向旋转90°得到，
∴AB＝AD，∠BAD＝90°，△ABC≌△ADE，
在Rt△ABD中，∠B＝∠ADB＝45°，
∴∠ADE＝∠B＝45°，
∴∠BDE＝∠ADB+∠ADE＝90°．
（2）①DF＝PF．
证明：由旋转的性质可知，AC＝AE，∠CAE＝90°，
在Rt△ACE中，∠ACE＝∠AEC＝45°，
∵∠CDF＝∠CAD，∠ACE＝∠ADB＝45°，
∴∠ADB+∠CDF＝∠ACE+∠CAD，
即∠FPD＝∠FDP，
∴DF＝PF．
②证明：过点P作PH∥ED交DF于点H，
∴∠HPF＝∠DEP，EPPF=DHHF，
∵∠DPF＝∠ADE+∠DEP＝45°+∠DEP，
∠DPF＝∠ACE+∠DAC＝45°+∠DAC，
∴∠DEP＝∠DAC，
又∵∠CDF＝∠DAC，
∴∠DEP＝∠CDF，
∴∠HPF＝∠CDF，
又∵FD＝FP，∠F＝∠F，
∴△HPF≌△CDF（ASA），
∴HF＝CF，
∴DH＝PC，
又∵EPPF=DHHF，
∴EPPF=PCCF．
16.（1）证明：∵四边形ABCD是矩形，∴∠B=∠C=∠D=90°，∴∠AFB+∠BAF=90°，
∵△AFE是△ADE翻折得到的，∴∠AFE=∠D=90°，∴∠AFB+∠CFE=90°，
∴∠BAF=∠CFE，∴△ABF∽△FCE．
（2）解：∵△AFE是△ADE翻折得到的，∴AF=AD=4，
∴BF=，∴CF=BC-BF=AD-BF=2，
由（1）得△ABF∽△FCE，∴，∴，∴EC=．
（3）
解：由（1）得△ABF∽△FCE，∴∠CEF=∠BAF=，∴tan+tan=，
设CE=1，DE=x，∵，∴AE=DE+2EC=x+2，AB=CD=x+1，AD=
∵△ABF∽△FCE，∴，∴，∴，
∴，∴，∴x2-4x+4=0，解得x=2，
∴CE=1，CF=，EF=x=2，AF= AD==，
∴tan+tan==．