2025高考数学二轮复习-专题2 平面向量、三角函数与解三角形 第4讲 解三角形【课件】

这是一份2025高考数学二轮复习-专题2 平面向量、三角函数与解三角形 第4讲 解三角形【课件】，共38页。PPT课件主要包含了基础回扣•考教衔接，以题梳点•核心突破，目录索引等内容，欢迎下载使用。
1.(人A必二6.4.3节例题改编)在△ABC中,c=1,a=2,C=30°,则A=(　　)A.60° B.90°C.45°D.120°
2.(人A必二6.4.3节习题改编)已知△ABC中,AB=3,BC=4,AC= ,则△ABC的面积等于(　　)
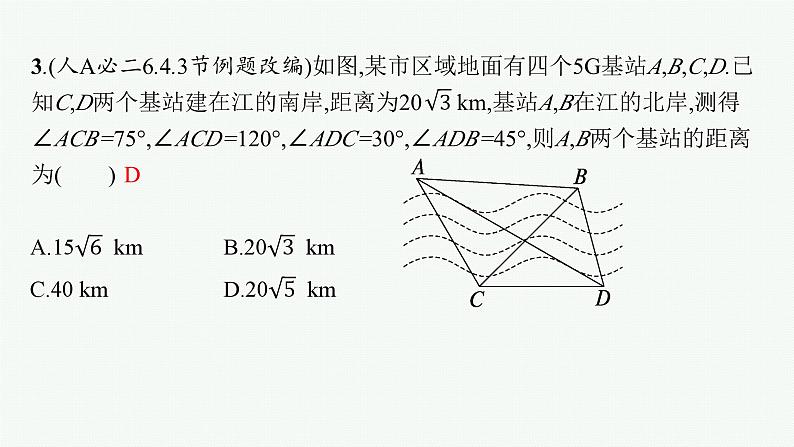
3.(人A必二6.4.3节例题改编)如图,某市区域地面有四个5G基站A,B,C,D.已知C,D两个基站建在江的南岸,距离为20 km,基站A,B在江的北岸,测得∠ACB=75°,∠ACD=120°,∠ADC=30°,∠ADB=45°,则A,B两个基站的距离为(　　)
4.(人A必二6.4.3节习题改编)在△ABC中,已知b=2,A=45°,C=75°,则c=　　　　　. 
1.(2023·全国乙,文4)记△ABC的内角A,B,C的对边分别为a,b,c,若acs B-bcs A=c,且C= ,则B=(　　)
解析 由acs B-bcs A=c及正弦定理,得sin Acs B-sin Bcs A=sin C,即sin(A-B)=sin C.又因为A,B,C是△ABC的内角,
2.(2023·北京,7)在△ABC中,(a+b)(sin A-sin C)=b(sin A-sin B),则C=(　　)
4.(2021·全国乙,理15)记△ABC的内角A,B,C的对边分别为a,b,c,面积为 ,B=60°,a2+c2=3ac,则b=　　　　　. 
考点一 正弦定理、余弦定理的直接应用
(2)(2024·福建厦门模拟)在△ABC中,内角A,B,C所对的边分别是a,b,c,已知b-c= a,2sin B=3sin C,则cs A=(　　)
[对点训练1](1)(2024·福建三明三模)已知a,b,c分别为△ABC三个内角A,B,C的对边,a=3,b= ,c=7,则A+C的值为(　　)
(2)(2024·山东青岛一模)△ABC内角A,B,C的对边分别为a,b,c,若b=2asin B,bc=4,则△ABC的面积为(　　)
考点二 三角形中的最值与范围问题
例2(2024·湖北武汉二模)在△ABC中,角A,B,C的对边分别为a,b,c,已知(2a-c)cs B-bcs C=0.(1)求B;
解 (1)∵(2a-c)cs B-bcs C=0,由正弦定理得(2sin A-sin C)cs B-sin Bcs C=0,2cs Bsin A-cs Bsin C-sin Bcs C=0,即2cs Bsin A=sin Bcs C+cs Bsin C,∴2cs Bsin A=sin(B+C)=sin A.∵A∈(0,π),∴sin A≠0,即cs B= .∵B∈(0,π),∴B= .
[对点训练2](2024·广东茂名一模)在△ABC中,内角A,B,C的对边分别是a,b,c,且bsin(B+C)=asin(1)求B的大小;(2)若D是边AC的中点,且BD=2,求△ABC面积的最大值.
考点三 解三角形的实际应用
例3(1)(2024·山东临沂一模)在同一平面上有相距14千米的A,B两座炮台,A在B的正东方.某次演习时,A向西偏北θ方向发射炮弹,B则向东偏北θ方向发射炮弹,其中θ为锐角,观测回报两炮弹皆命中18千米外的同一目标,接着A改为向西偏北 方向发射炮弹,弹着点为18千米外的点M,则B炮台与弹着点M的距离为(　　)A.7千米B.8千米C.9千米D.10千米
(2)(2024·江苏扬州模拟)小李同学打算用学到的解三角形知识测量某建筑物上面一座信号塔的高度.把塔底与塔顶分别看作点C,D,CD与地面垂直,小李先在地面上选取点A,B,测得AB=20 m,在点A处测得点C,D的仰角分别为30°, 60°,在点B处测得点D的仰角为30°,则塔CD高为　　　　　m. 
解析 在△ACD中,延长DC与BA的延长线交于点E,如图所示.
由题意可知,∠CAE=30°,∠DAE=60°,∠DBA=30°,所以A,B,E三点在同一条直线上,所以∠DAC=30°,∠DCA=120°,∠ADC=30°,∠BDA=30°,所以△ACD,△BAD为等腰三角形,即|CD|=|CA|,|AD|=|AB|.设|CD|=x,即|CA|=x,在△ACD中,由余弦定理得,|AD|2=|CD|2+|CA|2-2|CD||CA|cs∠DCA,
规律方法1.实际测量中的有关几个术语
2.解三角形实际应用题的步骤
[对点训练3](1)(2024·陕西西安模拟)在100 m高的楼顶A处,测得正西方向地面上B,C两点(B,C与楼底在同一水平面上)的俯角分别是75°和15°,则B,C两点之间的距离为(　　)
(2)(2024·广东湛江二模)为测量某大厦的高度,小张选取了大厦的一个最高点A,点A在大厦底部的射影为点O,两个测量基点B,C与O在同一水平面上,他测得BC=102 米,∠BOC=120°,在点B处测得点A的仰角为θ(tan θ=2),在点C处测得点A的仰角为45°,则该大厦的高度OA=　　　　　米.