2024-2025学年四川省成都市高一上册期末数学模拟检测试卷

这是一份2024-2025学年四川省成都市高一上册期末数学模拟检测试卷，共6页。
注意事项：
1．答第I卷前，考生务必将自己的班级、姓名、准考证号写在答题卷上．
2．每小题选出答案后，用铅笔把答题卷上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，答在试题卷上的无效．
一､单项选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合要求的．
1.已知集合，则( )

2.幂函数在上单调递增，则实数的值为（ ）

3.已知，则（ ）

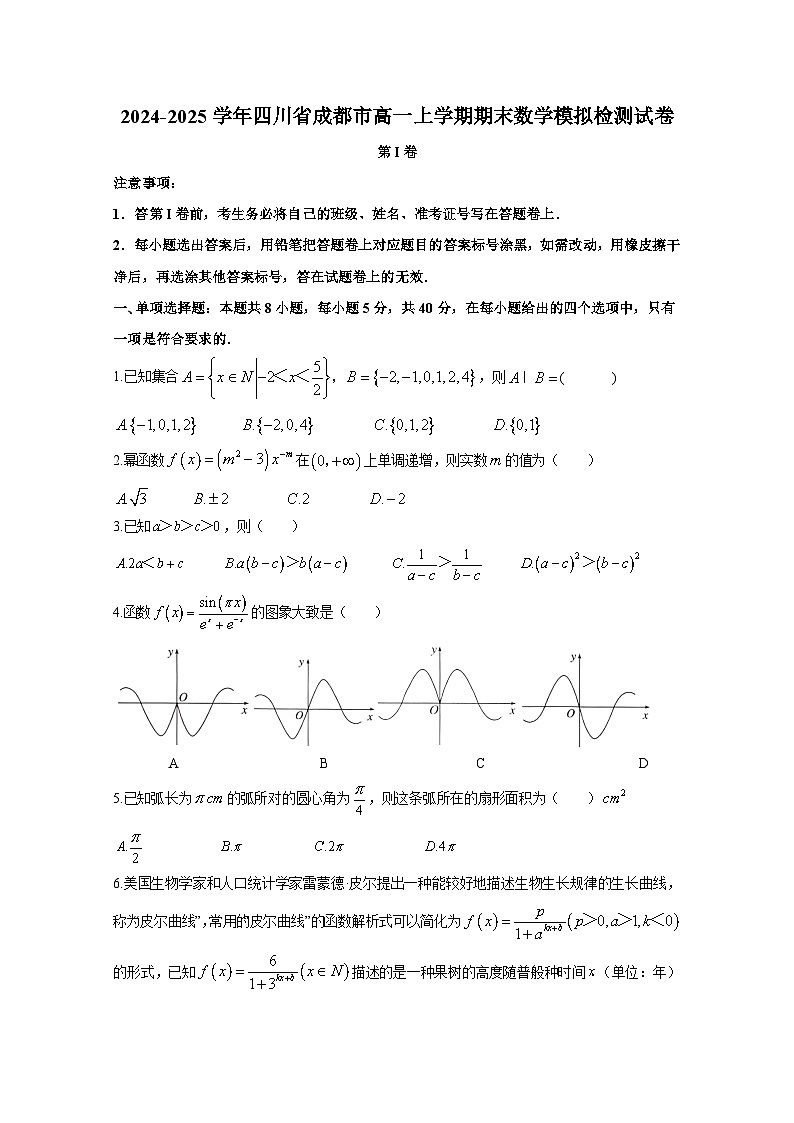
4.函数的图象大致是（ ）
A B C D
5.已知弧长为的弧所对的圆心角为，则这条弧所在的扇形面积为（ ）

6.美国生物学家和人口统计学家雷蒙德·皮尔提出一种能较好地描述生物生长规律的生长曲线，称为“皮尔曲线”，常用的“皮尔曲线”的函数解析式可以简化为 的形式，已知描述的是一种果树的高度随普般种时间（单位：年）变化的规律，若刚栽种（） 时该果树的高为，经过2年，该果树的高为，则该果树的高度不低于，至少需要（ ）
A.3年 B.4年 C.5年 D.6年
7.已知函数的值域为，则实数的取值范围为（ ）

8.已知函数是定义在上的偶函数，且在上单调递减，设，则的大小关系为（ ）

二､多项选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全选对的得6分，部分选对得部分分．
9.下列说法正确的是（ ）
A.“”是“”的充分不必要条件
B.“”是“”的必要不充分条件
C.“对任意一个无理数，也是无理数”是真命题
D.命题“”的否定是“”
10.对于函数，说法正确的是（ ）
A.若函数的定义域为，则实数的取值范围是
B.若函数的值域为，则实数
C.若函数在区间上为增函数，则实数的取值范围是
D.若，则不等式的解集为
11.设函数，则（ ）
A. 当时，函数有最小值为
B. 当时，函数是增函数
C. 当时，函数有最小值为4
D. 存在正实数，使得函数在上单调递增
第 = 2 \* ROMAN II卷
三、填空题：本大题共3小题，每小题5分，共计15分．
12. .
13.已知，且，则 .
14.已知函数，当时，关于的方程的解的个数为 .
四、解答题：本题共5个小题，其中15题13分，16，17题15分，18，19题17分，共77分.
15.已知
(1)化简；
(2)若是第三象限角，且，求的值；
16.若不等式的解集是.
（1）试求的值；
（2）求不等式的解集.
17.（2023成都七中期中）在经济学中，函数的边际函数定义为，某公司每月最多生产10台光刻机的某种设备，生产台（）这种设备的收入函数为（单位千万元），其成本函数为（单位千万元）.（以下问题请注意定义域）
（1）求收入函数的最小值；
（2）求成本函数的边际函数的最大值；
（3）求生产台光刻机的这种设备的的利润的最小值.
18.设为奇函数，为常数.
（1）求的值；
（2）证明在区间内单调递增；
（3）若对于区间上的每一个，不等式恒成立，求实数的取值范围.
19.函数的定义域为，若存在常数，使得对一切实数均成立，则称为“圆锥托底型”函数.
（1）判断是否为“圆锥托底型”函数？并说明理由；
（2）若是“圆锥托底型”函数，求出的最大值；
（3）问实数满足什么条件，是“圆锥托底型”函数.