数学七年级下册（2024）8.3 实数及其简单运算优质ppt课件

这是一份数学七年级下册（2024）8.3 实数及其简单运算优质ppt课件，文件包含83实数及其简单运算第1课时实数概念教学课件pptx、83实数及其简单运算第1课时实数概念教学设计docx、人教版2024七年级下册数学83实数及其简单运算同步练习含答案docx、83实数及其简单运算第1课时实数概念导学案docx等4份课件配套教学资源，其中PPT共33页， 欢迎下载使用。
3. 掌握利用数轴比较实数大小.
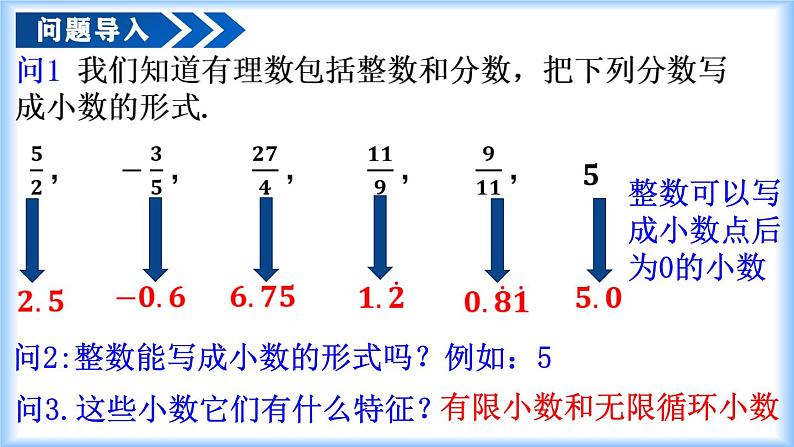
问2:整数能写成小数的形式吗？例如：5
问3.这些小数它们有什么特征？
有限小数和无限循环小数
整数可以写成小数点后为0的小数
有理数：有限小数或无限循环小数。任何一个有理数都可以写成有限小数或无限循环小数.反过来，任何有限小数或无限循环小数也都是有理数.
问4.所有的数都可以写成有限小数和无限循环小数的形式吗？
问5.这些小数它们又有什么特征？
无限不循环小数叫做无理数.
注意(1)类似①带根号的数不一定是无理数,带根号时还应注意根指数，(2)类似⑤⑥先化简再判断
无理数：无限不循环小数
有理数：有限小数或无限循环小数
问6.我们将有理数和无理数统称为实数，仿照有理数的分类吗？据此你能给出实数的其它分类吗？
有限小数或无限循环小数
无理数集合:{ …};有理数集合:{ …};正实数集合:{ …};负实数集合:{ …}.
对每个数都要进行判断，分类标准不同结果不同.
1.判断：(1).实数不是有理数就是无理数。（ ）(2).实数分为正实数和负实数。（ ）(3).无理数都是无限不循环小数。（ ）(4).无理数都是无限小数。（ ）(5).带根号的数都是无理数。（ ）(6).无理数一定都带根号。（ ）
问7.每个有理数都可以用数轴上的点表示，那么无理数是否也可以用数轴上的点来表示呢？
思考1： 如图，直径为１个单位长度的圆从原点沿数轴向右滚动一周，圆上一点从原点到达A点，则数轴上表示点A的数是多少？
(1)把两个边长为1的小正方形通过剪、拼，得到一个大正方形，大正方形的边长为 ，从而说明边长为1的小正方形的对角线为 .
(2)如下图，以一个单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B，数轴上A点和B点对应的数是什么？
数轴上的点有些表示有理数，有些表示无理数.每一个无理数都可以用数轴上的一个点来表示出来。每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一点都表示一个实数。
实数与数轴上的点是一一对应的
当点C为点B关于点A的对称点时，CA=BA数轴上两点间的距离的求法：数轴上两点间的距离等于表示这两点的数之差的绝对值．
(2)比较它们的大小（用“＜”号连接）
在数轴上表示的两个实数，右边的数总比左边的数大。
与有理数一样，在实数范围内：1.正数大于零，负数小于零，正数大于负数；2.两个正数，绝对值大的数较大；3.两个负数，绝对值大的数反而小.4.数轴上的点越往右表示的实数越大
有理数集合：{ …};无理数集合：{ …};正实数集合：{ …};负实数集合：{ …}.
作业：P54第1，2，3题