初中数学人教版（2024）七年级下册（2024）第七章 相交线与平行线7.2 平行线7.2.2 平行线的判定说课ppt课件

这是一份初中数学人教版（2024）七年级下册（2024）第七章 相交线与平行线7.2 平行线7.2.2 平行线的判定说课ppt课件，共27页。PPT课件主要包含了学习目标，解EFBC，理由如下，对顶角相等，等量代换，∴∠2∠3，∴b∥c，垂直的定义，解法1如图，解法2如图等内容，欢迎下载使用。
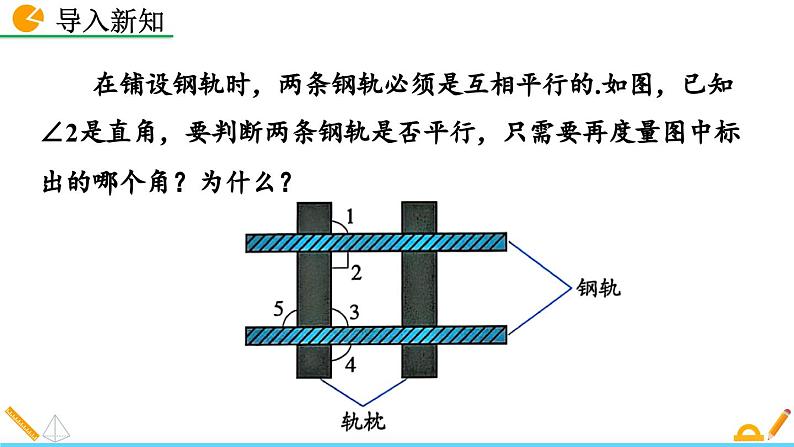
在铺设钢轨时，两条钢轨必须是互相平行的.如图，已知∠2是直角，要判断两条钢轨是否平行，只需要再度量图中标出的哪个角？为什么？
1. 进一步掌握平行线的判定方法，并会运用平行线的判定解决问题.
2. 掌握在同一平面内，垂直于同一条直线的两条直线互相平行.
3. 经历例题的分析过程，从中体会转化的思想和分析问题的方法，进一步培养推理能力.
例1 如图，直线EF与∠ABC的一边BA相交于D， ∠B+∠ADE=180°，EF与BC平行吗？ 为什么？
∵ ∠B+ ∠1=180°（ ）,
∠1= ∠2（ ）,
∴ ∠B+ ∠2=180°（ ）.
∴ EF∥BC（ ）.
同旁内角互补，两直线平行
平行线判定方法的灵活应用
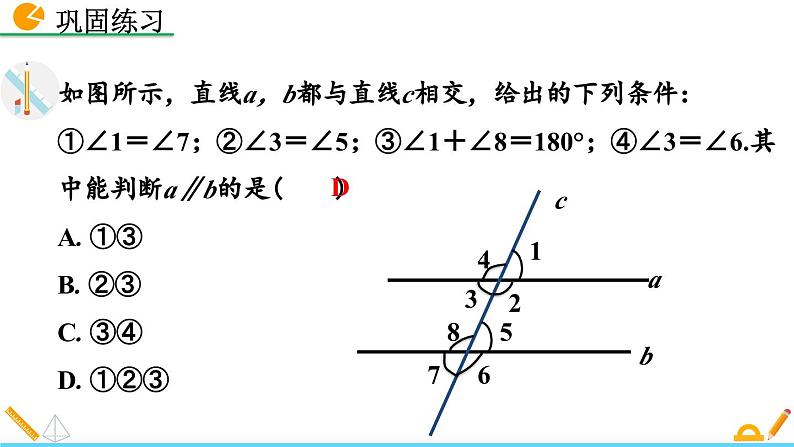
如图所示，直线a，b都与直线c相交，给出的下列条件：①∠1＝∠7；②∠3＝∠5；③∠1＋∠8＝180°；④∠3＝∠6.其中能判断a∥b的是( )A. ①③　 B. ②③C. ③④　 D. ①②③
例2 已知：如图，AB，CD都是直线， 且∠1=∠2，∠1=∠C，试说明AC∥FD.
∵ ∠1 = ∠2， ∠1 = ∠C （已知）,
∴ ∠2=∠C （等量代换）.
∴ AC∥FD （同位角相等，两直线平行）.
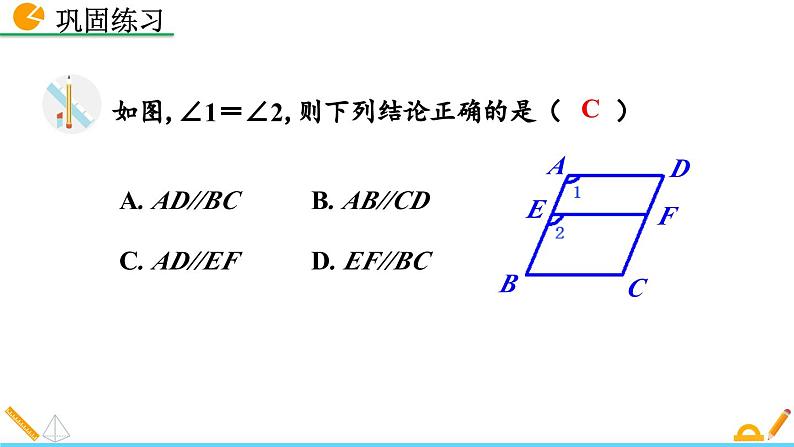
如图,∠1＝∠2,则下列结论正确的是（ ）
A. AD//BC B. AB//CD C. AD//EF D. EF//BC
解： AB∥CD .理由：∵ AC平分∠BAD，∴ ∠1=∠3 .∵∠1=∠2，∴ AB∥CD（内错角相等，两直线平行）.
例3 已知：如图，四边形ABCD中，AC平分∠BAD，∠1=∠2，AB与CD平行吗？为什么？
如图，∠1＝∠2，能判断AB∥DF吗？为什么？
答：添加∠CBD＝∠EDB.理由：∵ ∠1＝∠2， ∠CBD＝∠EDB，∴ ∠1+ ∠CBD ＝∠2+ ∠EDB，即∠ABD=∠BDF.∴AB∥DF（内错角相等，两直线平行）.
若不能判断AB∥DF，你认为还需要再添加的一个条件是什么呢？写出这个条件，并说明你的理由.
在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线平行吗？为什么？
猜想：在同一平面内，垂直于同一条直线的两条直线平行.
在同一平面内，垂直于同一条直线的两条直线平行
在同一平面内，b⊥a,c⊥a，试说明：b∥c.
∵b⊥a ，c ⊥a （已知）,
(同位角相等，两直线平行).
∴∠1= ∠2 = 90°
∵ b⊥a,c⊥a(已知),∴∠1=∠3=90°(垂直的定义).∴b∥c(内错角相等，两直线平行).
∵ b⊥a,c⊥a(已知),∴∠1=∠4=90°(垂直的定义).∴ ∠1+∠4=180°.∴b∥c(同旁内角互补，两直线平行).
在同一平面内，垂直于同一条直线的两条直线平行.
点拨：“在同一平面内，垂直于同一条直线的两条直线平行.”可以作为一种判定两直线平行的方法.

判定两直线平行的方法：1.判定方法1：同位角相等，两直线平行.2.判定方法2：内错角相等，两直线平行.3.判定方法3：同旁内角互补，两直线平行.4.平行线的定义.5.平行线基本事实的推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行.6.在同一平面内，垂直于同一条直线的两条直线平行.
如图，为了说明示意图中的平安大街与长安街是互相平行的，在地图上量得∠1=90°，你能通过度量图中已标出的其他的角来验证这个结论吗？说出你的理由.
解：方法1：测出∠3=90°，理由是同位角相等，两直线平行.方法2：测出∠2=90°，理由是同旁内角互补，两直线平行.方法3：测出∠5=90°，理由是内错角相等，两直线平行.方法4：测出∠2,∠3,∠4,∠5中任意一个角为90°，理由是同一平面内，垂直于同一条直线的两条直线平行.
如图所示，木工师傅在一块木板上画两条平行线，方法是用角尺画木板边缘的两条垂线，这样画的理由有下列4种说法：其中正确的是( )①同位角相等，两直线平行；②内错角相等，两直线平行；③同旁内角互补，两直线平行；④平面内垂直于同一直线的两条直线平行. A. ①②③ B. ①②④ C. ①③④ D.①③
（2020•湖南郴州中考）如图，直线a，b被直线c，d所截．下列条件能判定a∥b的是（　　）A．∠1=∠3B．∠2+∠4=180°C．∠4=∠5D．∠1=∠2
1. 如图所示，在下列条件中：①∠1＝∠2；②∠BAD＝∠BCD；③∠ABC＝∠ADC且∠3＝∠4；④∠BAD＋∠ABC＝180°，能判定AB∥CD的有 ( )A. 3个 B. 2个 C. 1个 D. 0个
2. 如图所示，下列条件：①∠1＝∠2；②∠A＝∠4；③∠1＝∠4；④∠A＋∠3＝180°；⑤∠C＝∠BDE，其中能判定AB∥DF的有( )A. 2个 B. 3个 C. 4个 D. 5个
3. 如图所示，已知∠A＝60°，下列条件能判定AB∥CD的是 ( )A. ∠C＝60° B. ∠E＝60° C. ∠AFD＝60° D. ∠AFC＝60°
4.如图, ∠B=∠C, ∠B+∠D=180°，那么BC平行DE吗？为什么？
∵ ∠B=∠C （ ）,
∠B+ ∠D=180°（ ）,
∴ ∠C+ ∠D=180°（ ）.
∴BC∥DE（ ）.
∵ ∠1=∠C （已知）,
∴ MN∥BC （内错角相等，两直线平行）.
∵ ∠2=∠B （已知）,
∴ EF∥BC （同位角相等，两直线平行）.
∴ MN∥EF （ ）.
5.已知：如图，∠1=∠C，∠2=∠B，试说明MN∥EF.
如果两条直线都与第三条直线平行，那么这两条直线也互相平行
如图所示，已知BE，EC分别平分∠ABC，∠BCD，且∠1与∠2互余，试说明AB∥DC.
解：∵∠1与∠2互余，∴∠1＋∠2＝90°.∵BE，EC分别平分∠ABC，∠BCD，∴∠ABC＝2∠1，∠BCD＝2∠2.∴∠ABC＋∠BCD＝2∠1＋2∠2＝2(∠1＋∠2)＝180°.∴AB∥DC.
如图，MF⊥NF于F，MF交AB于点E，NF交CD于点G，∠1＝140°，∠2＝50°，试判断AB和CD的位置关系，并说明理由．
解： AB∥CD.理由：过点F向左作FQ，使∠MFQ＝∠2＝50°，则∠NFQ＝∠MFN－∠MFQ＝90°－50°＝40°. ∴AB∥FQ. ∴∠1＋∠NFQ＝180°，∴CD∥FQ.
判定两条直线是否平行的方法有：
2.如果两条直线都与第三条直线平行，那么这两条直线也互相平行.
3.平行线的判定方法：
（1）同位角相等,两直线平行.
（2）内错角相等,两直线平行.
（3）同旁内角互补,两直线平行.
4.在同一平面内，垂直于同一条直线的两条直线平行.