第02讲 导数的运算-【寒假提升课】2025年高二数学寒假提升试题（人教A版2019）

这是一份第02讲 导数的运算-【寒假提升课】2025年高二数学寒假提升试题（人教A版2019），文件包含第02讲导数的运算思维导图+5知识点+六大考点+过关检测原卷版docx、第02讲导数的运算思维导图+5知识点+六大考点+过关检测解析版docx等2份试卷配套教学资源，其中试卷共33页， 欢迎下载使用。

一、基本初等函数的导数
二、导数的运算法则
1、加减法：
2、乘法：
3、除法：
三、复合函数的导数
1、复合函数的概念
一般地，对于两个函数和，如果通过中间变量，可以表示成的函数，那么称这个函数为和的复合函数，记作.
2、复合函数的求导法则
一般地，复合函数的导数和函数，的导数间的关系为，即y对x的导数等于y对u的导数与u对x的导数的乘积.
规律：从内到外层层求导，乘法连接。
3、求复合函数的导数的步骤
第一步分层：选择中间变量，写出构成它的内、外层函数；
第二步分别求导：分别求各层函数对相应变量的导数；
第三步相乘：把上述求导的结果相乘；
第四步变量回代：把中间变量代回。
4、求复合函数的导数注意以下几点：
（1）分解的函数通常为基本初等函数；
（2）求导时分清是对哪个变量求导；
（3）计算结果尽量简洁。
四、导函数的常用结论
1、奇函数的导数是偶函数，偶函数的导数是奇函数．周期函数的导数还是周期函数．
2、函数的导数反映了函数的瞬时变化趋势，其正负号反映了变化的方向，其大小反映了变化的快慢，越大，曲线在这点处的切线越“陡”．
五、求曲线“在”与“过”某点的切线
1、求曲线“在”某点处的切线方程步骤
第一步（求斜率）：求出曲线在点处切线的斜率
第二步（写方程）：用点斜式
第三步（变形式）：将点斜式变成一般式。
2、求曲线“过”某点处的切线方程步骤
第一步：设切点为；
第二步：求出函数在点处的导数；
第三步：利用Q在曲线上和，解出及；
第四步：根据直线的点斜式方程，得切线方程为．
【考点一：求简单函数的导数】
一、多选题
1．（23-24高二下·宁夏吴忠·阶段练习）下列求导错误的是（ ）
A．B．
C．D．
【答案】AB
【分析】根据求导公式和法则逐个分析判断即可.
【详解】对于A，，所以A错误，
对于B，，所以B错误，
对于C，，所以C正确，
对于D，，所以D正确，
故选：AB
2．（23-24高二下·广东茂名·期中）下列结论中不正确的有（ ）
A．若，则B．若，则
C．若，则D．若，则
【答案】ACD
【分析】根据基本初等函数的导数公式及导数的运算法则计算可得.
【详解】对于A：若，则，故A错误；
对于B：若，则，故B正确；
对于C：若，则，故C错误；
对于D：若，则，故D错误.
故选：ACD
3．（23-24高二下·河南南阳·期中）下列求导运算不正确的是（ ）
A．B．
C．D．
【答案】ACD
【分析】利用基本初等函数的导数公式和导数的四则运算法则求解即可．
【详解】A．，故符合题意；
B．，故不符合题意；
C．，故符合题意；
D．，故符合题意；
故选：ACD．
4．（22-23高三上·湖南衡阳·阶段练习）若函数的导函数的图象关于轴对称，则的解析式可能为( )
A．B．
C．D．
【答案】BCD
【分析】根据题意，依次求出选项中函数的导数，分析其导函数的奇偶性，据此分析可得答案．
【详解】根据题意，依次分析选项：
对于A，，其导数，其导函数为奇函数，图象不关于轴对称，不符合题意；
对于B，，其导数，其导函数为偶函数，图象关于轴对称，符合题意；
对于C，，其导数，其导函数为偶函数，图象关于轴对称，符合题意；
对于D，，其导数，其导函数是偶函数，图象关于轴对称，符合题意；
故选：BCD．
5．（23-24高二下·江苏无锡·阶段练习）下列命题正确的是（ ）
A．若，则
B．设函数，且，则
C．已知函数，则
D．
【答案】BD
【分析】由基本函数的导数公式求出各项的导数后，再逐项代入判断即可.
【详解】A：，故A错误；
B：，令，所以，故B正确；
C：，所以，故C错误；
D：，故D正确；
故选：BD.
【考点二：求复合函数的导数】
一、解答题
1．（23-24高二上·江苏·课前预习）指出下列函数的复合关系．
(1)；
(2)；
(3)；
(4)．
【答案】(1)，
(2)，，
(3)，
(4)，，
【分析】根据复合函数定义直接求解；
【详解】（1）对于，
可分解为，.
（2）对于，
可分解为，，.
（3）对于，
可分解为，.
（4）对于，
可分解为，，.
2．（25-26高二上·全国·课后作业）求下列函数的导数：
(1)；
(2)；
(3)；
(4)；
(5)；
(6).
【答案】(1)
(2)
(3)
(4)
(5)
(6)
【分析】结合导数的四则运算，利用复合函数求导法则求解各个函数即可.
【详解】（1）令，则.
.
（2）令，则，
.
（3）
,.
（4）令，则，
则.
（5），.
（6）.
3．（23-24高二上·江苏·课前预习）求下列函数的导数．
(1)；
(2)；
(3)；
(4)；
(5)；
(6)．
【答案】(1)
(2)
(3)
(4)
(5)
(6)
【分析】（1）利用复合函数求导运算求解即可；
（2）利用复合函数求导运算求解即可；
（3）利用复合函数求导运算求解即可；
（4）诱导公式和二倍角公式先化简，再直接求导；
（5）利用复合函数求导运算求解即可；
（6）利用复合函数求导运算求解即可.
【详解】（1）由，
则.
（2）由，
则.
（3）由，
则.
（4）由
，
则.
（5）由，
则.
（6）由，
则.
【考点三：求某点处的导数值】
一、单选题
1．（23-24高二下·江苏南京·开学考试）已知函数，则（ ）
A．0B．1C．D．
【答案】A
【分析】直接求导代入即可得解.
【详解】由题，，故.
故选：A.
2．（23-24高二下·河北承德·阶段练习）已知，则（ ）
A．B．C．D．
【答案】D
【分析】求导，直接代入求解即可.
【详解】由题意可得：，所以.
故选：D．
3．（24-25高二上·全国·课后作业）简谐运动是最基本也最简单的机械振动，其在声学、电子学、光学等领域有着重要的应用．经典力学的观点认为，当物体进行简谐运动时，其所受的合力与位移成正比．运用经典力学的理论进一步推演可知，简谐运动的位移是关于时间的正弦函数，若某质点做简谐运动，其位移关于时间的关系式为，则该质点的初速度大小为（ ）
A．B．C．D．
【答案】B
【分析】求导，根据导数的几何意义即可求解.
【详解】由可得，
易得该质点的速度为，所以该质点的初速度大小为．
故选：B
4．（23-24高二下·山东威海·期末）已知函数的导函数为，且，则（ ）
A．B．C．D．
【答案】B
【分析】求导可得，令，求解即可.
【详解】由，可得，
所以，解得.
故选：B.
5．（24-25高二下·全国·课后作业）已知函数，，，且，若，，，，则的值为（ ）
A．B．C．D．
【答案】B
【分析】由导数的除法公式即可得，令可得答案.
【详解】由已知得，
所以．
故选：B.
6．（23-24高二下·贵州安顺·期末）已知函数的导函数为，且满足，则的最大值为（ ）
A．B．0C．D．1
【答案】C
【分析】对给定等式求导，求出，进而求出函数的解析式及最大值.
【详解】由，求导得，
令x=0，则，即，
因此，当且仅当时取等号，
所以的最大值为.
故选：C
【考点四：求切线的斜率与方程】
一、单选题
1．（23-24高二下·天津·期中）曲线在点处的切线的倾斜角为（ ）
A．30°B．45°C．60°D．135°
【答案】D
【分析】首先求出导函数，再求出导数值，即可得到切线的斜率，从而得到切线的倾斜角.
【详解】因为，所以，
所以，所以曲线在点1,f1处的切线的斜率，
所以切线的倾斜角为.
故选：D.
2．（23-24高二下·陕西西安·期中）曲线在点处的切线方程为（ ）
A．B．C．D．
【答案】C
【分析】用导数几何意义去求切线方程即可.
【详解】由，得，
所以该曲线在点处的切线斜率为，
故所求切线方程为，
即．
故选：C.
3．（23-24高二上·云南昆明·期末）过点且与曲线相切的直线斜率为（ ）
A．B．C．1D．4
【答案】C
【分析】设出切点坐标，利用导数的几何意义求出切线方程，进而求出切线斜率.
【详解】设过点与曲线相切的切点坐标为，
由求导得：，则切线方程为，
于是，整理得，解得，
所以所求切线的斜率为1.
故选：C
二、填空题
4．（23-24高二下·吉林·期中）曲线在点处的切线方程为 ．
【答案】
【分析】求出函数的导数，并求出的值，再利用导数的几何意义求出切线方程.
【详解】由，求导得，则，
解得，于是，，
所以所求切线方程为，即.
故答案为：
5．（23-24高二下·河南洛阳·期中）曲线在点处的切线方程是 .
【答案】
【分析】求出原函数的导函数，得到函数在处的导数值，再求出，利用直线方程的斜截式得答案．
【详解】由，
得．
，
又，
曲线在点,处的切线方程是．
故答案为：．
【考点五：已知切线求参数范围】
一、单选题
1．（23-24高二下·陕西渭南·期中）已知曲线在点处的切线与直线垂直，则实数等于（ ）
A．B．C．1D．2
【答案】D
【分析】由导数的几何意义结合直线垂直斜率之间关系即可得到方程，求解即可.
【详解】因为，所以，
则曲线在点处的切线斜率为，
又因为直线斜率为，
所以，即.
故选：D.
2．（24-25高二上·全国·课后作业）函数的图象在点处的切线经过点，则（ ）
A．1B．C．eD．
【答案】A
【分析】借助导数的几何意义可得函数在点处的切线方程为，代入点计算即可得.
【详解】，故，
故函数在点处的切线方程为，
由在这条直线上，则，解得．
故选：A.
3．（23-24高二下·广东茂名·期中）设曲线在点处的切线与直线平行，则（ ）.
A．1B．2C．D．
【答案】B
【分析】根据导数的几何意义求解.
【详解】由函数，可得，则，
因为直线的斜率为2，可得.
故选：B.
4．（23-24高二下·安徽·阶段练习）若函数的图象在点处的切线方程为，则（ ）
A．13B．7C．4D．1
【答案】A
【分析】求出函数的导函数，依题意可得，即可得到方程组，求出、的值，再代入计算可得.
【详解】∵函数的图象在点1,f1处的切线方程为，
，，由题可知，，，
，，．
故选：A
二、填空题
5．（23-24高二下·江苏常州·期中）若函数的图象在点处的切线平行于轴，则 .
【答案】
【分析】求出原函数的导函数，利用处的导数值为0列式求解的值.
【详解】由，可得，
由题意得：，解得：，
故答案为：
6．（2024高三下·全国·专题练习）已知函数，若曲线在处的切线方程为，则 ．
【答案】
【分析】利用导函数和切线斜率求出的值，利用解析式和切点坐标求出的值，可得.
【详解】函数，，
若曲线在处的切线方程为，则切点坐标为，切线斜率，
则有，解得，
所以．
故答案为：.
7．（23-24高二下·安徽池州·期中）若点P是曲线上任一点，则点P到直线的最小距离是 ．
【答案】
【分析】当P为与直线平行且与曲线相切的切线的切点时，点P到直线的距离最短，根据导数几何意义求得点P坐标，最后根据点到直线距离公式得结果.
【详解】由可得，
设与直线平行，且与曲线相切的直线，对应切点坐标为，
则，解得，则，
则点到直线的距离，即为点P到直线的最小距离，
即为.
故答案为：.
8．（23-24高二下·天津滨海新·期末）已知，直线与曲线相切，则的最小值是 ．
【答案】25
【分析】根据题意设直线与曲线的切点为，进而根据导数的几何意义得，再根据基本不等式“1”的用法求解即可.
【详解】根据题意，设直线与曲线的切点为，
因为，直线的斜率为，
所以，，，
所以，
因为，
所以，当且仅当时等号成立.
所以的最小值是25.
故答案为：25.
【考点六：公切线问题】
寒假02讲素材06
一、单选题
1．（24-25高二上·全国·课后作业）若曲线在点处的切线也是曲线的切线，则（ ）
A．B．C．D．
【答案】D
【分析】先求出曲线在点处的切线方程,设切线与曲线的切点为，通过导数分别写出切线方程，由两条切线重合得出方程，再通过此方程有解得出结果.
【详解】的导数，令，则，
所以曲线在处的切线方程为，
即
的导数，设直线与曲线切于点，
则曲线在点处的切线方程为，
即，所以解得．
故选：D
2．（23-24高二下·江西吉安·期末）函数与函数公切线的斜率为（ ）
A．B．C．或D．或
【答案】C
【分析】先设切点分别为，并通过点斜式方程写出两条切线方程，根据公切线方程得，最后计算值即可.
【详解】设切点分别为，
且导数为，
所以切斜方程为既为，
也为，
所以，
且，
所以，
所以或，
所以公切线的斜率为或.
故选：C.
【点睛】关键点点睛：本题考查求公切线问题，解题关键是分别在函数上设不同切点并求切线方程，根据两切线方程一样来求解公切线斜率.
3．（24-25高二下·全国·课后作业）若曲线与曲线存在公共切线，则实数a的取值范围为（ ）
A．B．C．D．
【答案】D
【分析】设切点，根据导数求解斜率，可得和，进而将问题转化为与函数的图象有交点，即可根据导数求解.
【详解】由得，曲线在点处的切线斜率为
由得在点处的切线斜率为，
如果两条曲线存在公共切线，那么．
又由斜率公式可得，由此得到，则有解，
所以直线与函数的图象有交点即可．
当直线与函数的图象相切时，
设切点为，则，且，得，即有切点，此时，
故实数a的取值范围是．

故选：D．
二、多选题
4．（23-24高二下·河南南阳·期中）已知直线与曲线和都相切，切点分别为，则（ ）
A．B．
C．满足条件的直线有2条D．满足条件的直线只有1条
【答案】AC
【分析】分别求出切点Ax1,y1和切点切线方程，再由直线与两条曲线都相切，由两切线的斜率相等，且在y轴上的截距相等求解.
【详解】解：由题可知直线与曲线相切于点Ax1,y1，又，
所以直线的斜率，则在点处的切线方程为，
即，
直线与曲线相切于点
，则在点处的切线方程为，
即．
因为直线与两条曲线都相切，所以两条切线相同，
则且，
则，即，
可得，解得，故A正确，B错误；
把代入，得，
在同一坐标系中，作出函数的图象，如图所示：
由图象知：的值有两个，故C正确，D错误．
故选：AC
三、填空题
5．（2024·河北沧州·模拟预测）已知直线是曲线和的公切线，则实数a= ．
【答案】3
【分析】先设在上的切点，然后求出切点和切线，然后再设在上的切点，即可求出a的值.
【详解】设直线l与曲线相切于点，
由，得，因为l与曲线相切，
所以消去，得，解得．
设l与曲线相切于点，由，得，即，
因为是l与曲线的公共点，
所以消去，得，即，解得．
故答案为：3.
一、单选题
1．（23-24高二下·内蒙古巴彦淖尔·期末）下列求导正确的是（ ）
A．B．
C．D．
【答案】C
【分析】运用函数导数的四则运算和复合函数求导即可.
【详解】对于A，，故A错误；
对于B， ，故B错误；
对于C， ，故C正确；
对于D，，故D错误．
故选：C.
2．（24-25高二上·全国·课后作业）设函数，则（ ）
A．B．C．D．
【答案】D
【分析】运用复合函数的求导规则计算即可.
【详解】．
故选：D.
3．（23-24高二下·福建龙岩·期中）已知函数的导函数为，若，则（ ）
A．B．1C．D．
【答案】C
【分析】根据题意求导计算即可.
【详解】由函数，可得，
令，可得，解得，
所以，，.
故选：C.
4．（2024·河南新乡·一模）函数的图象在点处的切线方程是（ ）
A．B．C．D．
【答案】D
【分析】求出函数的导数，再利用导数的几何意义求出切线方程.
【详解】函数，求导得，则，而，
所以所求切线方程为，即.
故选：D
5．（23-24高二下·安徽合肥·期中）若曲线在点处的切线与直线垂直，则实数a的值为（ ）
A．1B．C．2D．3
【答案】D
【分析】求导，与直线垂直，求出的值.
【详解】由，求导，
则在点处的切线的斜率为，
而在点处的切线与直线垂直,
则，故.
故选：D
6．（2024高三·全国·专题练习）已知函数，若曲线y=fx在点处的切线方程为，则（ ）
A．B．C．D．
【答案】B
【分析】代点求解出，然后对函数进行求导，对应求解出，最后求解.
【详解】由已知，，
故，
，
则切线斜率为，故，
所以．
故选：B.
7．（2024高三·全国·专题练习）设函数，若直线是曲线的切线，则（ ）
A．B．C．D．
【答案】A
【分析】由曲线在切点处的斜率与直线的斜率相等，且切点同时位于曲线以及直线上建立方程组求解即可.
【详解】由题意，，
设直线与曲线的切点为，
则，解得．
将代入，解得．
故选：A
8．（24-25高三上·山西·阶段练习）曲线与的公切线的斜率为（ ）
A．B．C．D．
【答案】A
【分析】根据导数的几何意义分别求fx,gx的切线，结合题意列式求解即可.
【详解】因为，则，
设切点坐标为，切线斜率为，
可得切线方程为，即；
因为，则，
设切点坐标为，切线斜率为，
可得切线方程为，即；
由题意可得：，解得，
所以公切线的斜率为.
故选：A.
9．（2024高三·全国·专题练习）已知P是曲线（）上的动点，点Q在直线上运动，则当取最小值时，点P的横坐标为（ ）
A．B．C．D．
【答案】C
【分析】画出曲线（）和直线的图象，将所求距离问题转化为两平行线距离最小，从而结合两直线平行，利用导数的几何意义列方程即可求得切点的横坐标.
【详解】画出曲线（）和直线的图象，如下图所示

若使得取最小值，
则曲线在点处的切线与直线平行，
对函数求导得，令，可得，
又，解得．
故选：C
二、多选题
10．（2024高三·全国·专题练习）下列求导运算正确的是（ ）
A．B．
C．D．
【答案】BC
【分析】根据基本函数的导数公式及复合函数导数求法判断各项正误.
【详解】由为常数，则，A错误；
由，则，B正确；
由，C正确；
由，D错误．
故选：BC
11．（25-26高二上·全国·课后作业）（多选）以下求导运算正确的有（ ）
A．若，则
B．若，则
C．若，则
D．若，则
【答案】ACD
【分析】利用导数的运算法则，即可判断选项.
【详解】A项，，则，A正确；
B项，，，B错误；
C项，，，C正确；
D项，，，D正确．
故选：ACD
三、填空题
12．（2024高三·全国·专题练习）曲线的一条切线经过点，则该切线的斜率为 .
【答案】
【分析】设切点为，利用导数几何意义及斜率两点式列方程求，即可得切线斜率.
【详解】因为，所以，设切点为，则，
所以，解得，所以，即切线的斜率为.
故答案为：
13．（2024高三·全国·专题练习）已知函数，若曲线在点处的切线过坐标原点，则实数的值为 ．
【答案】
【分析】首先对函数求导，然后表示出在点的切线方程，最后根据切线过原点求出实数.
【详解】因为，所以．
又，
所以曲线在点处的切线方程为,
又该切线过坐标原点，所以，即，
解得:．
故答案为：.
14．（23-24高三上·山东临沂·开学考试）已知，，若与的图象在交点处的切线重合，则 ．
【答案】/
【分析】设与的图象交点为，再根据导数的几何意义列方程化简求解即可.
【详解】设与的图象交点为，则，即，故.
又则，解得，则.
故答案为：
15．（2024高三·全国·专题练习）写出曲线过坐标原点的切线方程： ， .
【答案】
【分析】分和两种情况，当时设切点为，求出函数的导函数，即可求出切线的斜率，从而表示出切线方程，再根据切线过坐标原点求出，即可求出切线方程，当时同理可得；
【详解】因为，
当时，，设切点为，由，得，
所以切线方程为.
又切线过坐标原点，所以，解得，
所以切线方程为，即；
当时，，设切点为，由，得，
所以切线方程为.
又切线过坐标原点，所以，解得，
所以切线方程为，即.
故答案为：；.
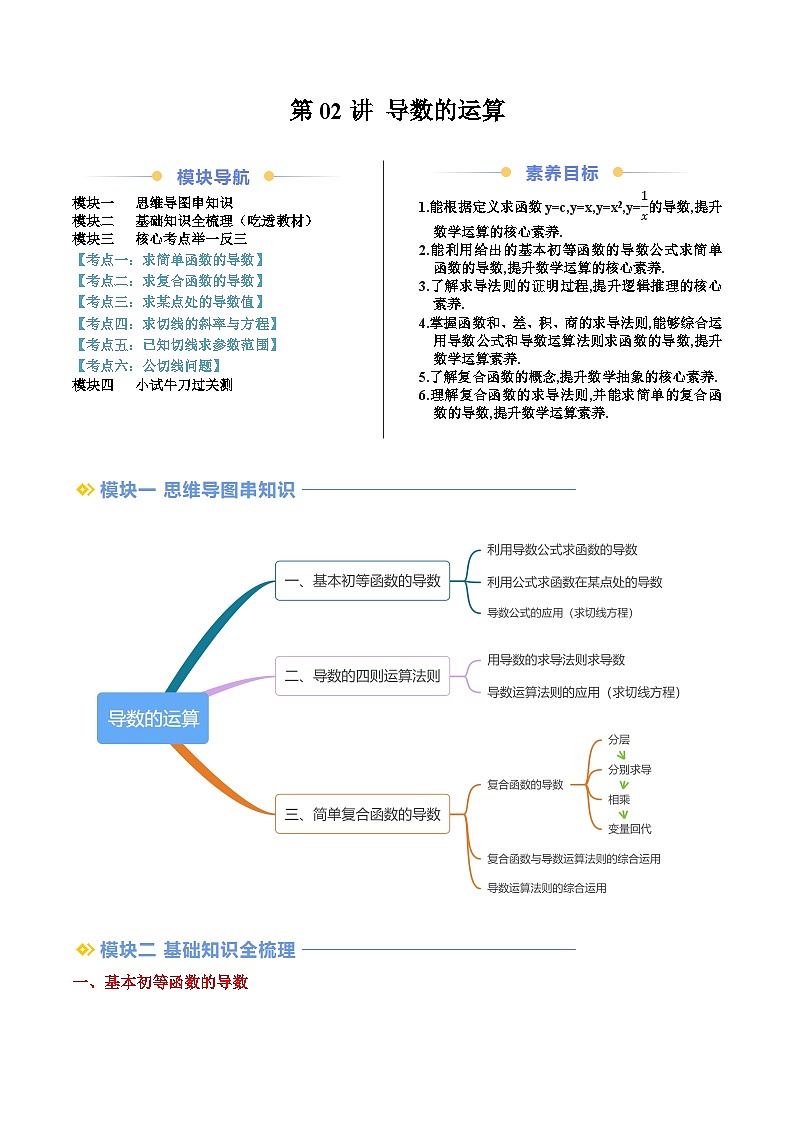
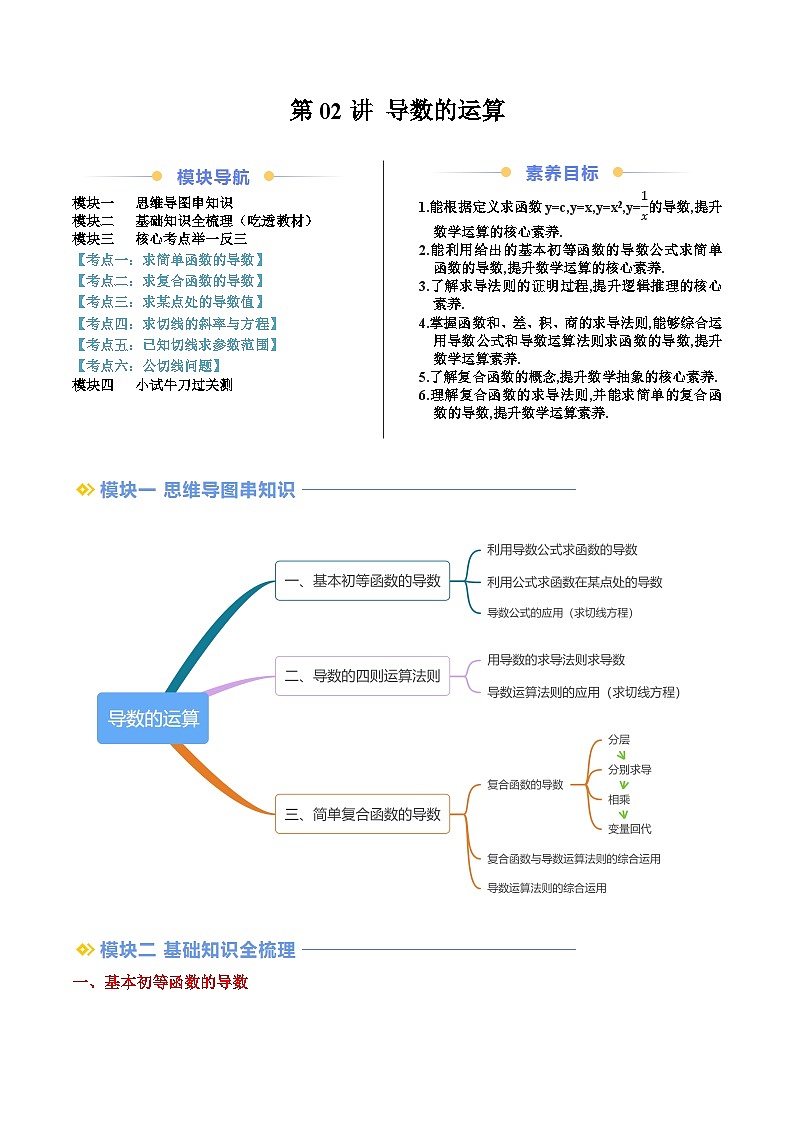
模块一 思维导图串知识
模块二 基础知识全梳理（吃透教材）
模块三 核心考点举一反三
【考点一：求简单函数的导数】
【考点二：求复合函数的导数】
【考点三：求某点处的导数值】
【考点四：求切线的斜率与方程】
【考点五：已知切线求参数范围】
【考点六：公切线问题】
模块四 小试牛刀过关测
1.能根据定义求函数y=c,y=x,y=x2,y=1x的导数,提升数学运算的核心素养.
2.能利用给出的基本初等函数的导数公式求简单函数的导数,提升数学运算的核心素养.
3.了解求导法则的证明过程,提升逻辑推理的核心素养.
4.掌握函数和、差、积、商的求导法则,能够综合运用导数公式和导数运算法则求函数的导数,提升数学运算素养.
5.了解复合函数的概念,提升数学抽象的核心素养.
6.理解复合函数的求导法则,并能求简单的复合函数的导数,提升数学运算素养.
函数
导函数
函数
导函数
(c是常数)
(为实数)
特别地
特别地