人教版数学八年级上册期中复习 专题11 三角形中的特殊模型-高分线模型、双（三）垂直模型（2份，原卷版+解析版）

这是一份人教版数学八年级上册期中复习 专题11 三角形中的特殊模型-高分线模型、双（三）垂直模型（2份，原卷版+解析版），文件包含人教版数学八年级上册期中复习专题11三角形中的特殊模型-高分线模型双三垂直模型原卷版doc、人教版数学八年级上册期中复习专题11三角形中的特殊模型-高分线模型双三垂直模型解析版doc等2份试卷配套教学资源，其中试卷共40页， 欢迎下载使用。
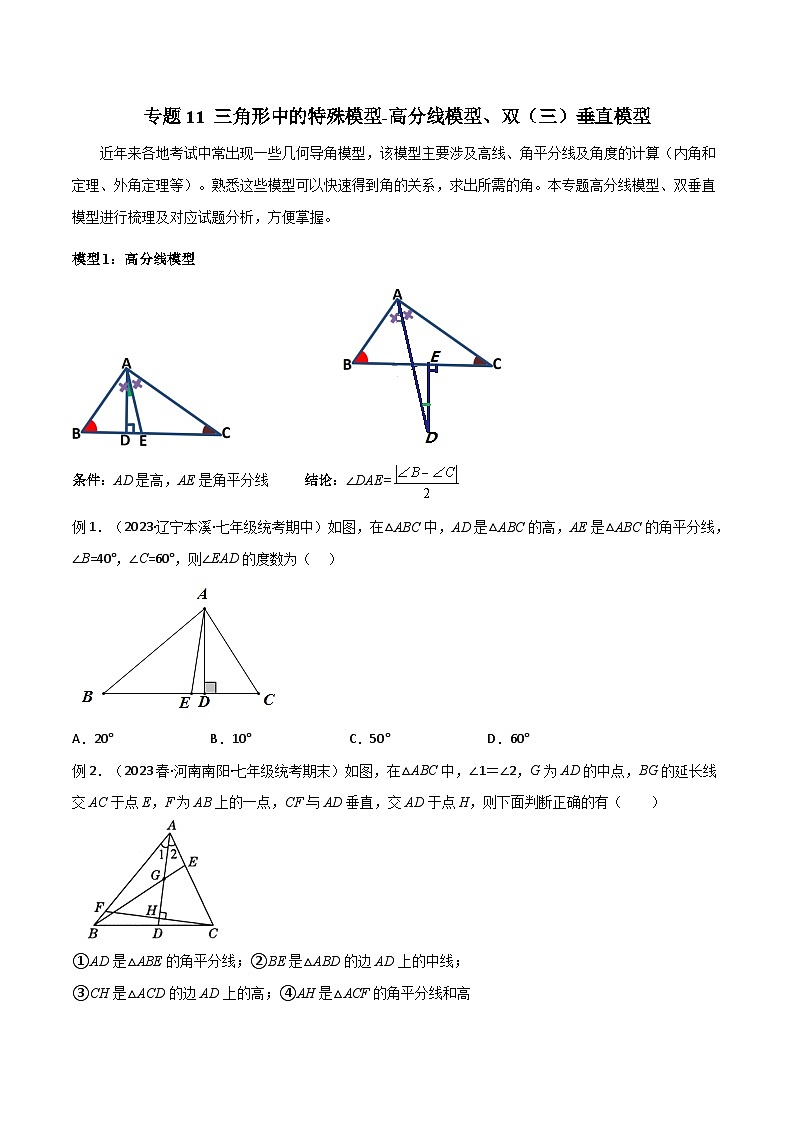
模型1：高分线模型

条件：AD是高，AE是角平分线 结论：∠DAE=
例1．（2023·辽宁本溪·七年级统考期中）如图，在△ABC中，AD是△ABC的高，AE是△ABC的角平分线，∠B=40°，∠C=60°，则∠EAD的度数为（ ）
A．20°B．10°C．50°D．60°
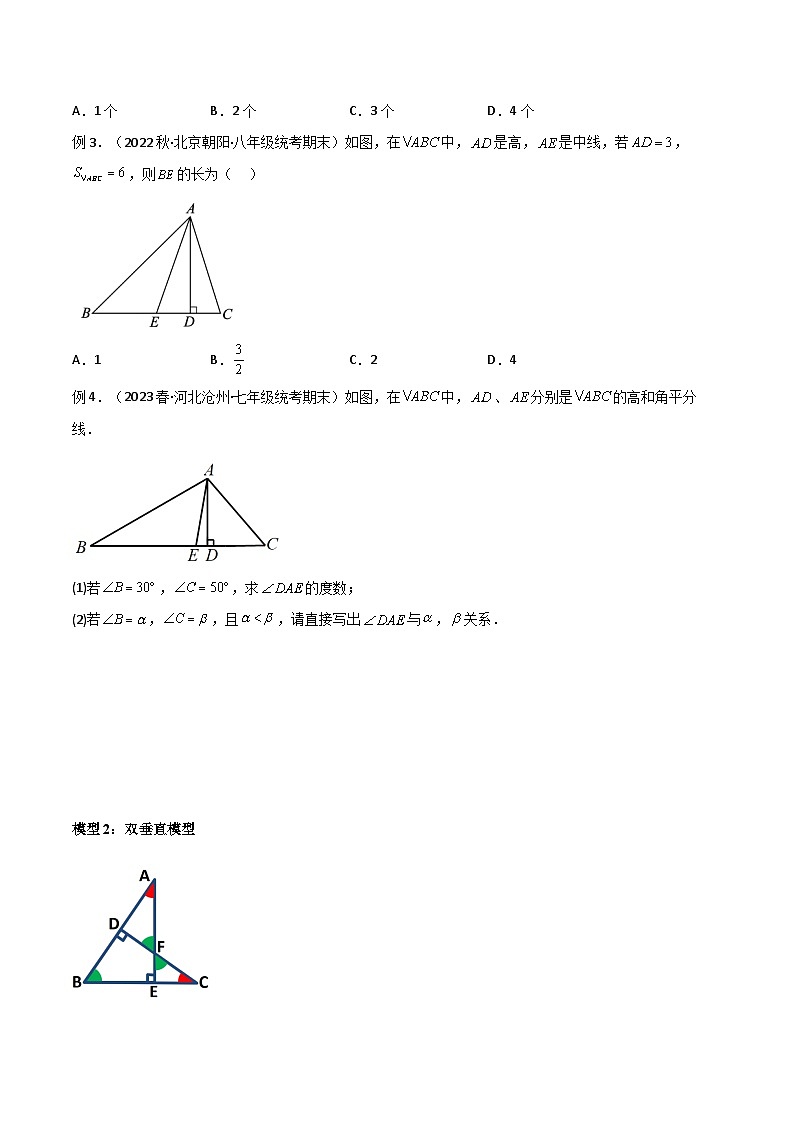
例2．（2023春·河南南阳·七年级统考期末）如图，在△ABC中，∠1＝∠2，G为AD的中点，BG的延长线交AC于点E，F为AB上的一点，CF与AD垂直，交AD于点H，则下面判断正确的有（ ）
①AD是△ABE的角平分线；②BE是△ABD的边AD上的中线；
③CH是△ACD的边AD上的高；④AH是△ACF的角平分线和高
A．1个B．2个C．3个D．4个
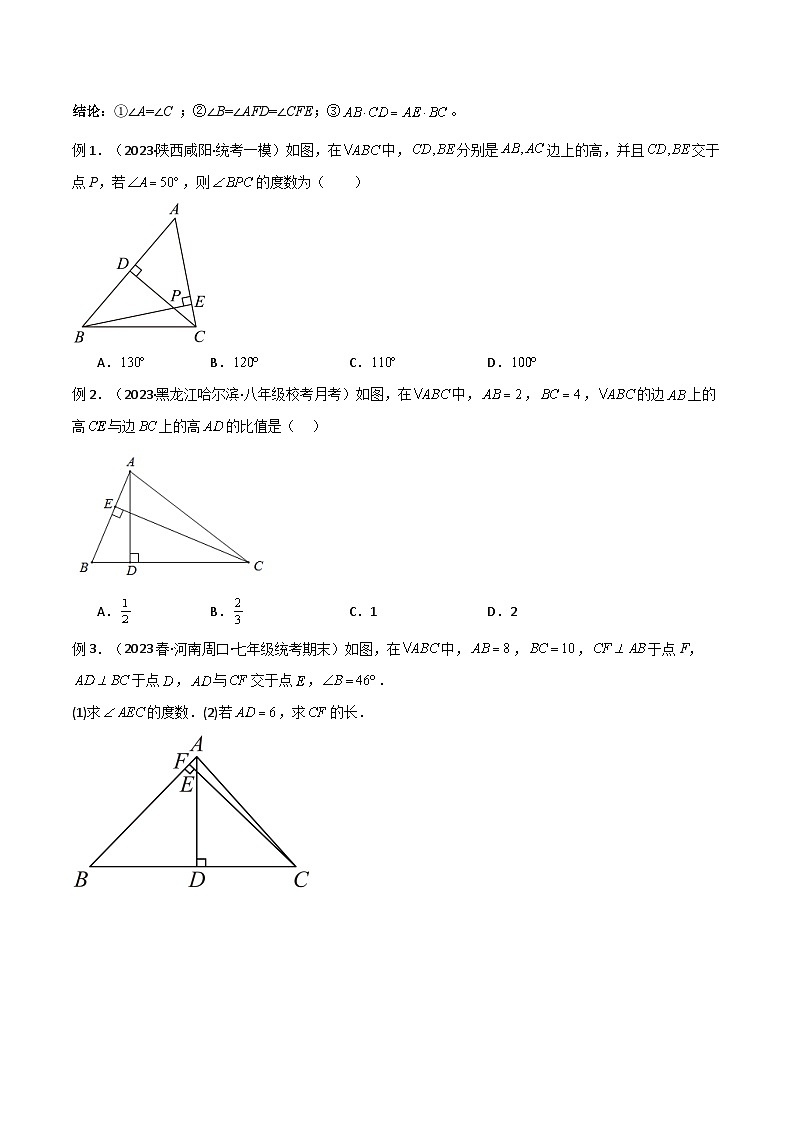
例3．（2022秋·北京朝阳·八年级统考期末）如图，在中，是高，是中线，若，，则的长为（ ）
A．1B．C．2D．4
例4．（2023春·河北沧州·七年级统考期末）如图，在中，、分别是的高和角平分线．
(1)若，，求的度数；
(2)若，，且，请直接写出与，关系．
模型2：双垂直模型
结论：①∠A=∠C ；②∠B=∠AFD=∠CFE；③。
例1．（2023·陕西咸阳·统考一模）如图，在中，分别是边上的高，并且交于点P，若，则的度数为（ ）

A．B．C．D．
例2．（2023·黑龙江哈尔滨·八年级校考月考）如图，在中，，，的边上的高与边上的高的比值是（ ）
A．B．C．1D．2
例3．（2023春·河南周口·七年级统考期末）如图，在中，，，于点F，于点，与交于点，．
(1)求的度数．(2)若，求的长．

模型3：子母型双垂直模型(射影定理模型)
结论：①∠B=∠CAD；②∠C=∠BAD；③。
例1．（2023·广东广州·七年级校考阶段练习）如图，在中，，于D，求证：．
例2．（2023·云南玉溪·八年级校考期中）如图所示，在△ACB中，∠ACB＝90°，∠1＝∠B．
(1)求证：CD是△ABC的高；(2)如果AC＝8，BC＝6，AB＝10，求CD的长．
例3．（2022秋·北京通州·八年级统考期末）如图，在中，，，垂足为．如果，，则的长为（ ）
A．2B．C．D．
例4．（2023春·江苏泰州·七年级统考期末）已知：如图，在中，，、分别在边、上，、相交于点．
(1)给出下列信息：①；②是的角平分线；③是的高．请你用其中的两个事项作为条件，余下的事项作为结论，构造一个真命题，并给出证明；
条件：______，结论：______．（填序号）
证明：
(2)在（1）的条件下，若，求的度数．（用含的代数式表示）

课后专项训练
1．（2023春·云南文山·七年级校联考期末）如图，AE，AD分别是的高和角平分线，，，则的度数为（ ）
A．40°B．20°C．10°D．30°
2．（2023·绵阳市八年级月考）如图，在中，平分交于点、平分交于点，与相交于点，是边上的高，若，，则的度数为（ ）
A．B．C．D．
3．（2023春·江苏宿迁·七年级统考期末）如图，在中，，、分别是的高和角平分线，点E为边上一点，当为直角三角形时，则 ．

4．（2023秋·重庆·八年级专题练习）如图，在中，，平分，若，，则 ．
5．（2023·江苏八年级校考课时练习）已知：如图，AC⊥BC，垂足为C，∠BCD是∠B的余角
求证：∠ACD=∠B
证明：∵AC⊥BC（已知）
∴∠ACB=90°（ ）
∴∠BCD是∠DCA的余角
∵∠BCD是∠B的余角（已知）
∴∠ACD=∠B（ ）
6．（2023春·河南新乡·七年级校考期末）如图，是直角三角形，，于点D，是的角平分线，过点D作交于点G，求证：．请补全下面的证明过程．
证明：∵（已知），
∴（_____），
∴（直角三角形两锐角互余），
∵（已知），
∴（直角三角形两锐角互余），
∵是的角平分线，，
∴（______），
∴（______），
∵（______），
∴（等量代换），
∵（已知），
∴（______），
∴（______）．
7．（2023春·陕西咸阳·八年级统考期中）如图，在中，，于点D，平分交于点E，交于点F，求证：．

8．（2023春·四川乐山·七年级统考期末）如图，在直角中，，是斜边上的高，，求：

（1）的度数；（2）的度数．
对于上述问题，在以下解答过程的空白处填上适当的内容（理由或数学式）
解：（1）∵，（已知），
又∵（______），
∴（______）．
（2）∵（______），
∴（等式的性质）．
∵（已知），
∴（垂直定义）．
∴______（等量代换）．
9．（2022秋·辽宁抚顺·八年级统考期末）如图所示，在中，，平分．
(1)求的度数；(2)求的度数；(3)直接写出，，三个角之间的数量关系．
10．（2023·上海闵行·七年级校考阶段练习）如图，已知的两条高相交于点，，，求的度数．
11．（2022秋·山东威海·七年级校联考期中）如图，是的高，E是上一点，交于F，且有，，试说明．

12．（2022春·江苏·七年级专题练习）如图所示，在中，已知于D，于E，，，求的大小．

13．如图所示，在中，是高，、是角平分线，它们相交于点，，，求、的度数.
14．（2022秋·广东东莞·八年级校考期中）如图，在中，为的高，为的角平分线，交于点G，比大，，求的大小．
15．（2023秋·山东·八年级专题练习）如图，已知在中，，于点．

（1）尺规作图：作的平分线交于点，交于点；（要求：保留作图痕迹，不写作法，不下结论）
（2）在（1）的条件下，求证：．
__________
又__________
__________
__________
平分
__________
．
16．（2023春·黑龙江·七年级校考期中）如图，中，，平分，，．
(1)求的度数．(2)直接写出图中四对相等的锐角，

17．（2023春·陕西榆林·七年级统考期末）如图，是的角平分线，是的边上的中线．
(1)若的周长为13，，，求的长度；
(2)若，的面积为10，，求点到的距离．

18．（2023·江苏·七年级统考期末）已知：如图，中，在的延长线上取一点，作于点（1）如图①，若于点，那么是的平分线吗？若是，请说明理由．请完成下列证明并在下面的括号内填注依据
解：是，理由如下：
（已知）
（垂直定义）
（ ）
（两直线平行，同位角相等）
（ ）
（已知）
（等量代换）
平分（ ）
（2）如图②，若中的角平分线相交于点．
①求证：
②随着的变化，的大小会发生变化吗﹖如果有变化，请直接写出与的数量关系；如果没有变化，请直接写出的度数．