人教版数学八年级上册期中复习 专题02 全等模型-一线三等角（K字）模型（2份，原卷版+解析版）

这是一份人教版数学八年级上册期中复习 专题02 全等模型-一线三等角（K字）模型（2份，原卷版+解析版），文件包含人教版数学八年级上册期中复习专题02全等模型-一线三等角K字模型原卷版doc、人教版数学八年级上册期中复习专题02全等模型-一线三等角K字模型解析版doc等2份试卷配套教学资源，其中试卷共46页， 欢迎下载使用。
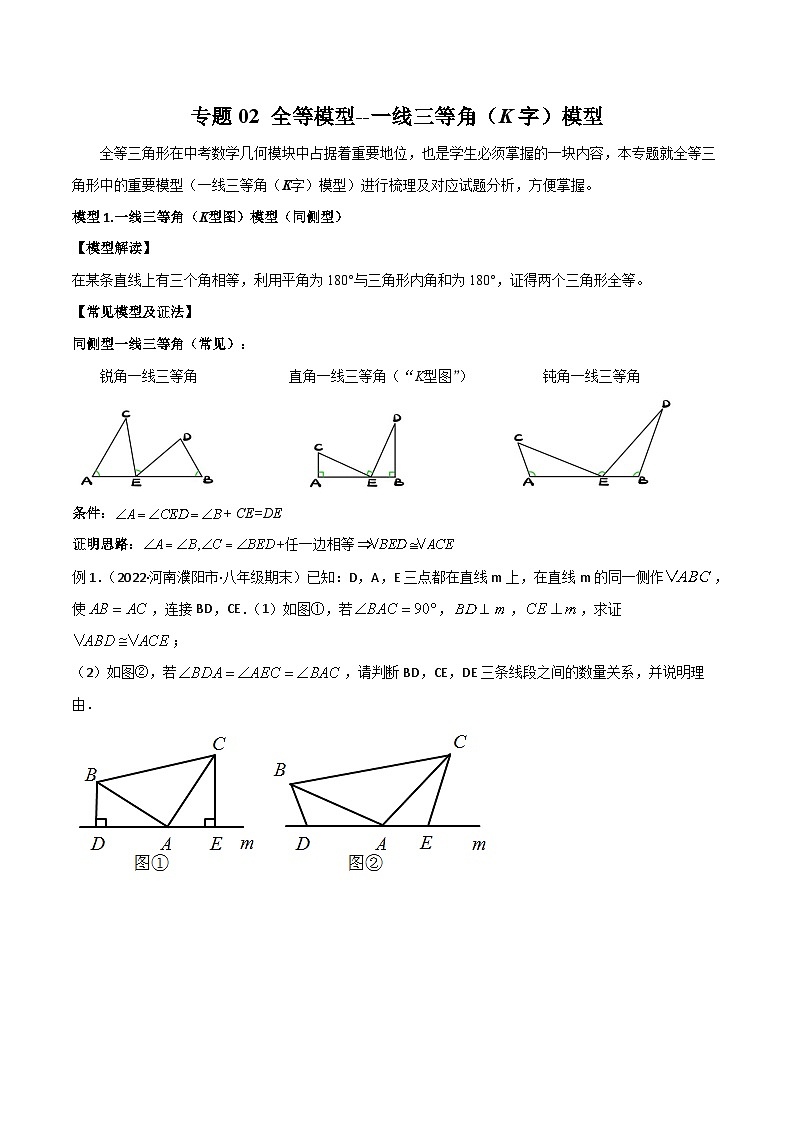
模型1.一线三等角（K型图）模型（同侧型）
【模型解读】
在某条直线上有三个角相等，利用平角为180°与三角形内角和为180°，证得两个三角形全等。
【常见模型及证法】
同侧型一线三等角（常见）：
锐角一线三等角 直角一线三等角（“K型图”） 钝角一线三等角

条件：+ CE=DE
证明思路：+任一边相等
例1．（2022·河南濮阳市·八年级期末）已知：D，A，E三点都在直线m上，在直线m的同一侧作，使，连接BD，CE．（1）如图①，若，，，求证；
（2）如图②，若，请判断BD，CE，DE三条线段之间的数量关系，并说明理由．
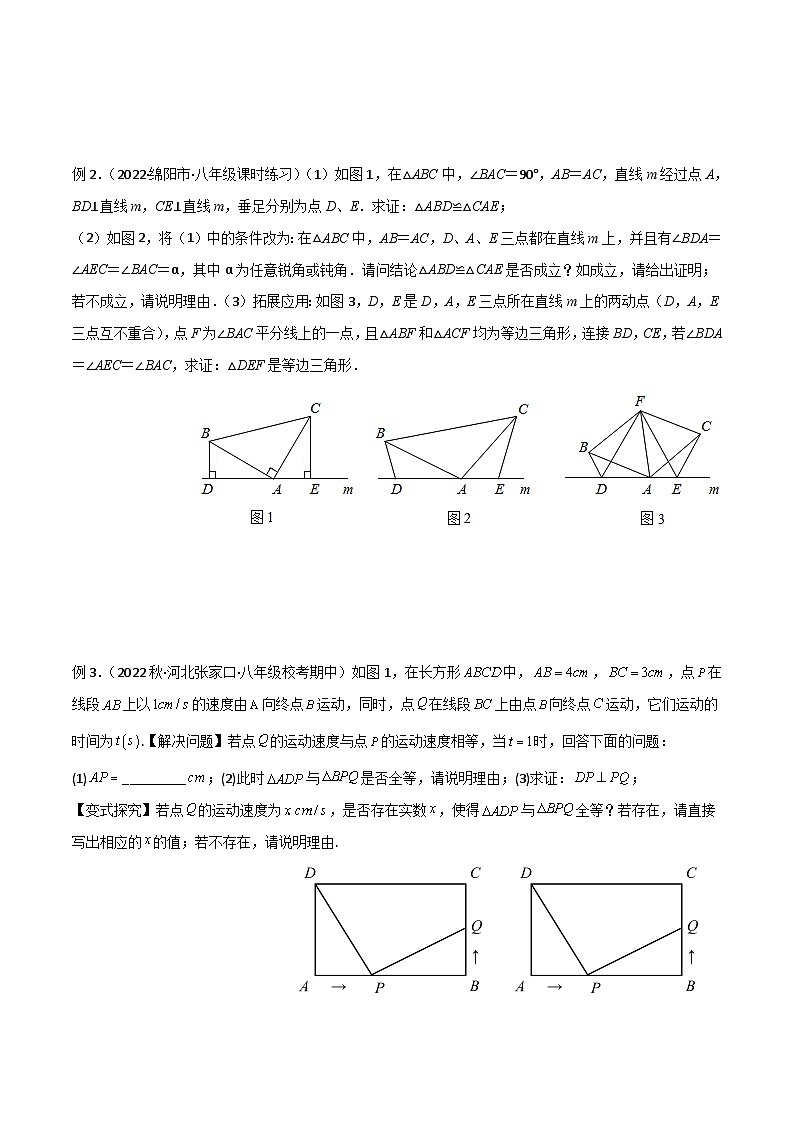
例2．（2022·绵阳市·八年级课时练习）（1）如图1，在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．求证：△ABD≌△CAE；
（2）如图2，将（1）中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC＝α，其中α为任意锐角或钝角．请问结论△ABD≌△CAE是否成立？如成立，请给出证明；若不成立，请说明理由．（3）拓展应用：如图3，D，E是D，A，E三点所在直线m上的两动点（D，A，E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD，CE，若∠BDA＝∠AEC＝∠BAC，求证：△DEF是等边三角形．
例3．（2022秋·河北张家口·八年级校考期中）如图1，在长方形中，，，点在线段上以的速度由向终点运动，同时，点在线段上由点向终点运动，它们运动的时间为.【解决问题】若点的运动速度与点的运动速度相等，当时，回答下面的问题：
(1)；(2)此时与是否全等，请说明理由；(3)求证：；
【变式探究】若点的运动速度为，是否存在实数，使得与全等？若存在，请直接写出相应的的值；若不存在，请说明理由.
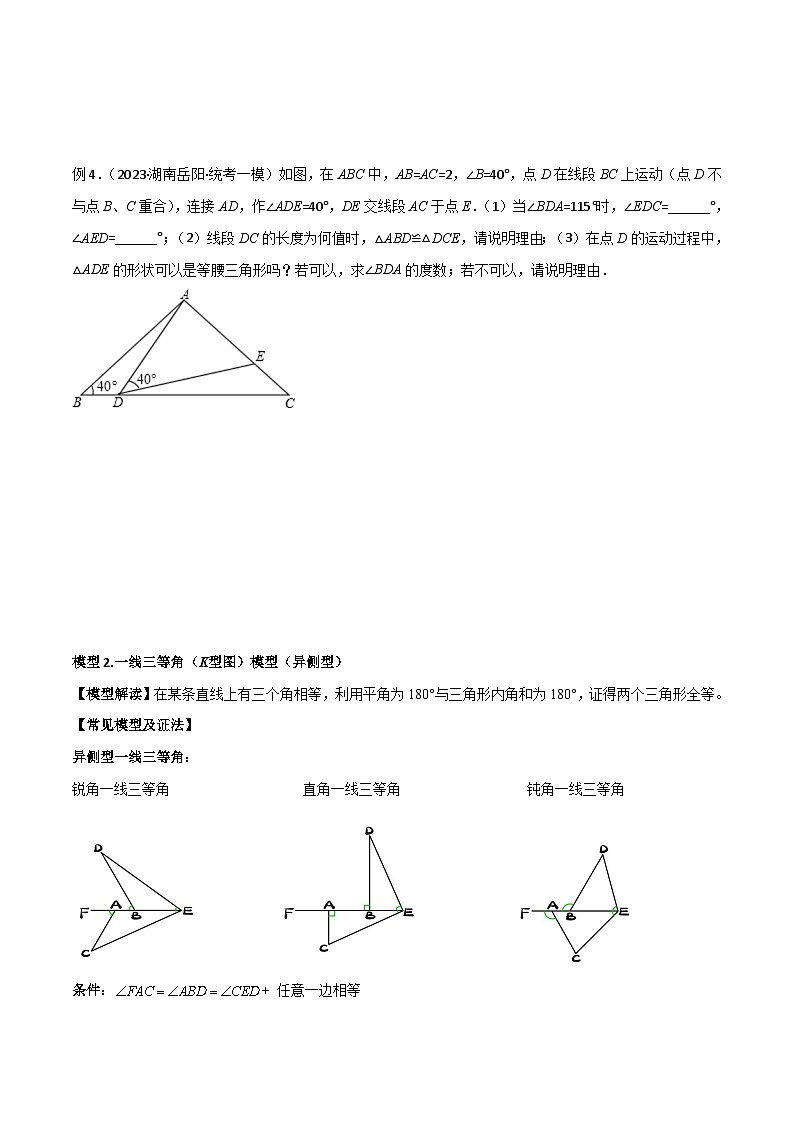
例4．（2023·湖南岳阳·统考一模）如图，在ABC中，AB=AC=2，∠B=40°，点D在线段BC上运动（点D不与点B、C重合），连接AD，作∠ADE=40°，DE交线段AC于点E．（1）当∠BDA=115°时，∠EDC=______°，∠AED=______°；（2）线段DC的长度为何值时，△ABD≌△DCE，请说明理由；（3）在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，求∠BDA的度数；若不可以，请说明理由．
模型2.一线三等角（K型图）模型（异侧型）
【模型解读】在某条直线上有三个角相等，利用平角为180°与三角形内角和为180°，证得两个三角形全等。
【常见模型及证法】
异侧型一线三等角：
锐角一线三等角 直角一线三等角 钝角一线三等角

条件：+ 任意一边相等
证明思路：+任一边相等
例1．（2023春·广西·七年级专题练习）问题1：在数学课本中我们研究过这样一道题目：如图1，∠ACB＝90°，AC＝BC，BE⊥MN，AD⊥MN，垂足分别为E、D．图中哪条线段与AD相等？并说明理由．
问题2：试问在这种情况下线段DE、AD、BE具有怎样的等量关系？请写出来，不需要说明理由．
问题3：当直线CE绕点C旋转到图2中直线MN的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并说明理由．
例2．（2022秋·河北承德·八年级统考期末）如图1一直角三角板，，，过点C的直线l不经过三角形内部，过点A、B作，，垂足分别为D，E．
(1)请你在图1中写出一对全等三角形：___________ (2)请证明你所写结论．
(3)尝试探究：若，；①图1中四边形的面积为：________（用含a，b的代数式表示，）
②图2中过点C的直线l经过三角形内部，其它不变，则四边形的面积为：___________（用含a，b的代数式表示，）
例3．（2023·江苏·八年级假期作业）在中，，直线经过点C，且于D，于E．
(1)当直线绕点C旋转到图1的位置时，求证：①；②．
(2)当直线绕点C旋转到图2的位置时，求证：；(3)当直线绕点C旋转到图3的位置时，试问具有怎样的等量关系？请写出这个等量关系，并加以证明．
课后专项训练
1．（2023·浙江·八年级假期作业）如图，在△ABC中，AB＝AC＝9，点E在边AC上，AE的中垂线交BC于点D，若∠ADE＝∠B，CD＝3BD，则CE等于（ ）
A．3B．2C．D．
2．（2023·江苏·八年级假期作业）如图，在中，，分别过点B，C作过点A的直线的垂线BD，CE，垂足为D，E．若，求DE的长．

3．（2022秋·绵阳市八年级课时练习）阅读下面材料：小明遇到这样一个问题：如图1，△ABC中，∠A＝90°，∠B＝30°，点D，E分别在AB，BC上，且∠CDE＝90°．当BE＝2AD时，图1中是否存在与CD相等的线段？若存在，请找出并加以证明，若不存在，说明理由．小明通过探究发现，过点E作AB的垂线EF，垂足为F，能得到一对全等三角形（如图2），从而将解决问题．
请回答：（1）小明发现的与CD相等的线段是 ．（2）证明小明发现的结论．
4.（2022·黑龙江牡丹江·九年级期末）平面内有一等腰直角三角板（∠ACB＝90°）和一直线MN．过点C作CE⊥MN于点E，过点B作BF⊥MN于点F．当点E与点A重合时（如图1），易证：AF+BF＝2CE．
(1)当三角板绕点A顺时针旋转至图2的位置时，上述结论是否仍然成立？若成立，请给予证明；若不成立，线段AF、BF、CE之间又有怎样的数量关系，请直接写出你的猜想，不需证明．
(2)当三角板绕点A顺时针旋转至图3的位置时，上述结论是否仍然成立？若成立，请给予证明；若不成立，线段AF、BF、CE之间又有怎样的数量关系，请直接写出你的猜想，不需证明．
5．（2023春·上海·七年级专题练习）通过对数学模型“K字”模型或“一线三等角”模型的研究学习，解决下列问题：[模型呈现]如图1，，，过点B作于点C，过点D作于点E．求证：．
[模型应用]如图2，且，且，请按照图中所标注的数据，计算图中实线所围成的图形的面积为________________．
[深入探究]如图3，，，，连接，，且于点F，与直线交于点G．若，，则的面积为_____________．
6．（2022秋·广东广州·八年级校考阶段练习）已知：CD是经过∠BCA的顶点C的一条直线，CA＝CB，E、F是直线CD上两点，∠BEC＝∠CFA＝∠α．
（1）若直线CD经过∠BCA的内部，∠BCD＞∠ACD．①如图1，∠BCA＝90°，∠α＝90°，写出BE，EF，AF间的等量关系： ．②如图2，∠α与∠BCA具有怎样的数量关系，能使①中的结论仍然成立？写出∠α与∠BCA的数量关系 ．（2）如图3．若直线CD经过∠BCA的外部，∠α＝∠BCA，①中的结论是否成立？若成立，进行证明；若不成立，写出新结论并进行证明．
7．（2023·上海浦东新·八年级校考期中）在中，，，点在直线上（，除外），的垂线与的垂线交于点，研究和的数量关系.（1）在探究，的关系时，运用“从特殊到一般”的数学思想，发现当点是的中点时，只需要取边的中点（如图），通过推理证明就可以得到的数量关系，请你按照这种思路直接写出和的数量关系：_______________。（2）当点是线段上（，除外）任意一点（其它条件不变），上面得到的结论是否仍然成立呢？证明你的结论；（3）点在线段的延长线上，上面得到的结论是否仍然成立呢？在下图中画出图形，并证明你的结论.

8．（2022·黑龙江牡丹江·九年级期末）平面内有一等腰直角三角板（∠ACB＝90°）和一直线MN．过点C作CE⊥MN于点E，过点B作BF⊥MN于点F．当点E与点A重合时（如图1），易证：AF+BF＝2CE．
(1)当三角板绕点A顺时针旋转至图2的位置时，上述结论是否仍然成立？若成立，请给予证明；若不成立，线段AF、BF、CE之间又有怎样的数量关系，请直接写出你的猜想，不需证明．
(2)当三角板绕点A顺时针旋转至图3的位置时，上述结论是否仍然成立？若成立，请给予证明；若不成立，线段AF、BF、CE之间又有怎样的数量关系，请直接写出你的猜想，不需证明．
9．（2022·河南商丘市·九年级期末）如图（1），已知中，，；是过的一条直线，且，在的异侧，于，于．（1）求证：；（2）若直线绕点旋转到图（2）位置时（），其余条件不变，问与，的数量关系如何？请给予证明．（3）若直线绕点旋转到图（3）位置时（），其余条件不变，问与，的数量关系如何？请直接写出结果，不需证明；（4）根据以上的讨论，请用简洁的语言表达直线在不同位置时与，的位置关系．
10．（2023春·上海·七年级专题练习）已知为等腰三角形，，直线过点（不经过点），过点作于点，过点作于点．
(1)如图1，当点位于直线的同侧时，判断与的大小关系，并说明理由；
(2)如图2，若点位于直线的两侧，①（1）的结论是否还能成立，请说明理由；
②设与交于点，当时，判断与是否相等，并说明理由．

11．（2023春·上海·七年级专题练习）（1）观察理解：
如图1，∠ACB＝90°，AC＝BC，直线l过点C，点A，B在直线l同侧，BD⊥l，AE⊥l，垂足分别为D，E，求证：△AEC≌△CDB． （2）理解应用：如图2，过△ABC边AB、AC分别向外作正方形ABDE和正方形ACFG，AH是BC边上的高，延长HA交EG于点I．利用（1）中的结论证明：I是EG的中点．
（3）类比探究：①将图1中△AEC绕着点C旋转180°得到图3，则线段ED、EA和BD的关系_______；
②如图4，直角梯形ABCD中，，AB⊥BC，AD＝2，BC＝3，将腰DC绕D点逆时针旋转90°至DE，△AED的面积为 ．


12．（2022·安徽·九年级期末）如图，Rt△ACB中，∠ACB＝90°，AC＝BC，E点为射线CB上一动点，连结AE，作AF⊥AE且AF＝AE．（1）如图1，过F点作FD⊥AC交AC于D点，求证：FD＝BC；
（2）如图2，连结BF交AC于G点，若AG＝3，CG＝1，求证：E点为BC中点．
（3）当E点在射线CB上，连结BF与直线AC交子G点，若BC＝4，BE＝3，则 ．（直接写出结果）
13．（2022秋·八年级课时练习）在综合实践课上，李老师以“含30°的三角板和等腰三角形纸片”为模具与同学们开展数学活动．已知，在等腰纸片中，，，将一块含30°角的足够大的直角三角尺（，）按如图所示放置，顶点在线段上滑动（点不与，重合），三角尺的直角边始终经过点，并与的夹角，斜边交于点．
（1）当时，______°；
（2）当等于何值时，？请说明理由；
（3）在点的滑动过程中，存在是等腰三角形吗？若存在，请求出夹角的大小；若不存在，请说明理由．
14．（2023·重庆江津·八年级统考期末）（1）问题：如图①，在四边形中，，是上一点，，．求证：；
（2）问题：如图②，在三角形中，，是上一点，，且．求的值．
15．（2023春·绵阳市·八年级专题练习）如图，线段AB=6，射线BG⊥AB，P为射线BG上一点，以AP为边做正方形APCD，且点C、D与点B在AP两侧，在线段DP上取一点E，使得∠EAP=∠BAP，直线CE与线段AB相交于点F（点F与点A、B不重合），
（1）求证：△AEP≌△CEP；
（2）判断CF与AB的位置关系，并说明理由；
（3）△AEF的周长是否为定值，若是，请求出这个定值，若不是，请说明理由．