人教版数学九上期中复习专题22.5 高频题型专题：二次函数的图象信息题之五大考点（2份，原卷版+解析版）

这是一份人教版数学九上期中复习专题22.5 高频题型专题：二次函数的图象信息题之五大考点（2份，原卷版+解析版），文件包含人教版数学九上期中复习专题225高频题型专题二次函数的图象信息题之五大考点原卷版doc、人教版数学九上期中复习专题225高频题型专题二次函数的图象信息题之五大考点解析版doc等2份试卷配套教学资源，其中试卷共44页， 欢迎下载使用。
目录
TOC \ "1-3" \h \u \l "_Tc27382" 【典型例题】 PAGEREF _Tc27382 \h 1
\l "_Tc13376" 【考点一 二次函数与一次函数图象共存问题】 PAGEREF _Tc13376 \h 1
\l "_Tc28904" 【考点二 二次函数与反比例函数图象共存问题】 PAGEREF _Tc28904 \h 6
\l "_Tc9097" 【考点三 含字母参数的二次函数的图象和性质】 PAGEREF _Tc9097 \h 11
\l "_Tc31555" 【考点四 二次函数的图象和性质与系数a,b,c的问题】 PAGEREF _Tc31555 \h 16
\l "_Tc26862" 【考点五 二次函数的图象与几何动点问题】 PAGEREF _Tc26862 \h 26
【典型例题】
【考点一 二次函数与一次函数图象共存问题】
例题：（2023·安徽合肥·统考三模）在同一平面直角坐标系内，二次函数与一次函数的图像可能是（ ）
A． B． C． D．
【变式训练】
1．（2023·全国·九年级专题练习）如图，已知二次函数与一次函数，它们在同一直角坐标系中的图象大致是（ ）
A． B． C． D．
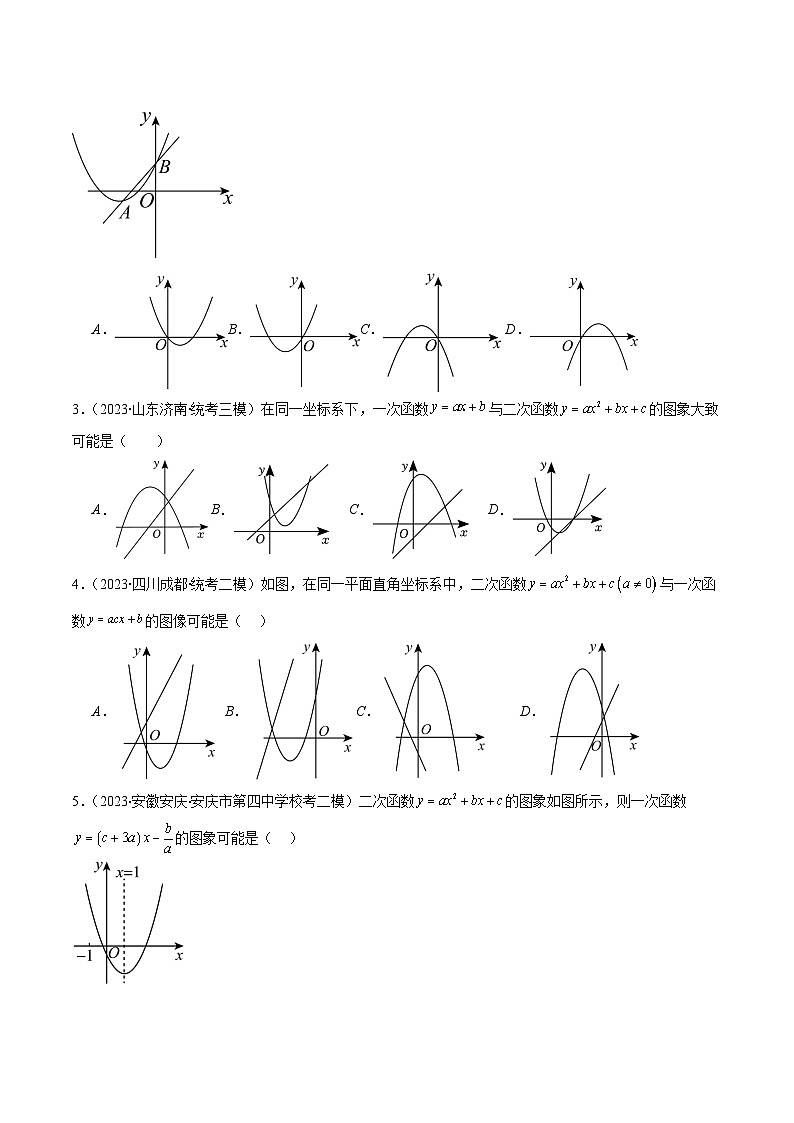
2．（2023·全国·九年级专题练习）已知抛物线和直线分别交于A点和B点，则抛物线的图象可能是（ ）

A．B．C． D．
3．（2023·山东济南·统考三模）在同一坐标系下，一次函数与二次函数的图象大致可能是（ ）
A．B．C．D．
4．（2023·四川成都·统考二模）如图，在同一平面直角坐标系中，二次函数与一次函数的图像可能是（ ）
A． B．C． D．
5．（2023·安徽安庆·安庆市第四中学校考二模）二次函数的图象如图所示，则一次函数的图象可能是（ ）

A． B． C． D．
6．（2023·山东青岛·统考二模）如图，二次函数的图象开口向下，且经过第二象限的点P．若点P的横坐标为，则一次函数的图象大致如（ ）

A． B． C． D．
【考点二 二次函数与反比例函数图象共存问题】
例题：（2023·湖北襄阳·统考一模）如图，二次函数与反比例函数在同一平面直角坐标系内的图象可能是（ ）
A．B．C．D．
【变式训练】
1．（2023·浙江·九年级假期作业）二次函数与反比例函数在同一平面直角坐标系中的图像可能是（ ）
A．B． C． D．
2．（2023·山东东营·统考二模）二次函数（）的图象如图所示，则一次函数（）与反比例函数（）在同一平面直角坐标系中的图象大致是（ ）
A．B．C．D．
3．（2022秋·安徽蚌埠·九年级校考期中）已知二次函数（b，c是常数）的图象如图所示，则一次函数与反比例函数在同一坐标系内的大致图象是（ ）
A．B．C．D．
4．（2023秋·广西南宁·九年级校联考阶段练习）已知二次函数y＝ax2+bx+c的部分函数图象如图所示，则一次函数与反比例函数在同一平面直角坐标系中的图象大致是（ ）
A．B．C．D．
5．（2023·山东青岛·统考三模）二次函数的图象如图所示，则一次函数与反比例函数在同一坐标系内的图象大致为（ ）
A．B．C．D．
【考点三 含字母参数的二次函数的图象和性质】
例题：（2023·全国·九年级专题练习）已知二次函数，下列说法正确的是( )
A．点在该函数的图象上 B．当且时，
C．该函数的图象与x轴一定有交点 D．当时，该函数图象的对称轴一定在直线的左侧
【变式训练】
1．（2023·江苏扬州·统考中考真题）已知二次函数（a为常数，且），下列结论：
①函数图像一定经过第一、二、四象限；②函数图像一定不经过第三象限；③当时，y随x的增大而减小；④当时，y随x的增大而增大．其中所有正确结论的序号是( )
A．①②B．②③C．②D．③④
2．（2023·江苏南京·校考三模）已知整式，下列关于整式的值的结论：
①的值可能为；
②当时，的值随的增大而增大；
③当为小于的实数时，的值大于；
④不存在这样的实数，使得的值小于．
其中所有正确结论的序号是（ ）
A．①③B．①②④C．②③④D．①②③④
3．（2023·湖北武汉·统考一模）已知函数为实数，下列四个结论：
当时，图象与坐标轴所夹的锐角为；
若，则当时，随着的增大而减小；
不论为何值，若将函数图象向左平移个单位长度，则图象经过原点；
当时，抛物线顶点在第一象限．
其中正确的结论是 （填写序号）
4．（2023春·福建福州·八年级福建省福州延安中学校考期末）对于二次函数．有下列说法：
①若，则二次函数的图象与y轴的负半轴相交；
②若，当时，y有最大值3；
③若a为整数，且二次函数的图象与x轴的两个公共点都为整数点，则a的值只能等于1；
④若，且为该函数图象上的三点，则．
其中正确的是 ．（只需填写序号）
【考点四 二次函数的图象和性质与系数a,b,c的问题】
例题：（2023春·湖南长沙·八年级校联考期末）某二次函数的部分图象如图所示，下列结论中一定成立的有（ ）
①；②；③； ④．

A．个B．个C．个D．个
【变式训练】
1．（2023春·山东德州·九年级德州市第十中学校考阶段练习）如图，二次函数的图像的顶点在第一象限，且过点和，下列结论：①，②，③，④，⑤当时，．其中正确结论的个数是（ ）

A．个B．个C．个D．个
2．（2023·四川成都·统考一模）如图，已知二次函数的图象与x轴交于A，B两点，与y轴交于点C，，对称轴为直线，则下列结论：①；②；③；④是关于x的一元二次方程的一个根．其中正确的有（ ）个．
A．4B．3C．2D．1
3．（2023秋·山东东营·九年级东营市胜利第一初级中学校考期末）如图，二次函数的图象关于直线对称，与轴交于，两点，若，则下列四个结论：①；②；③（为任意实数）；④．正确结论的个数为（ ）

A．1个B．2个C．3个D．4个
4．（2023·广东汕尾·校考模拟预测）已知二次函数的图象的一部分如图所示，其中对称轴为：，下列结论：①；②；③；④；上述结论中正确结论的个数为（ ）
A．1个B．2个C．3个D．4个
5．（2023春·四川达州·九年级校考阶段练习）二次函数的部分图象如图所示，图象过点，对称轴为直线，下列结论：①；②；③；④已知、在该二次函数图像上，当且时，都有．其中正确的结论有 ．（填序号）

6．（2023·全国·九年级假期作业）如图，二次函数的图象过点，对称轴为直线．有以下结论：
①；
②；
③（m为任意实数）；
④若，是抛物线上的两点，当时，；
⑤若方程的两根为，，且，则．
其中正确的是 ．（填写序号）
【考点五 二次函数的图象与几何动点问题】
例题：（2023·河南周口·河南省淮阳中学校考三模）如图，在中，．动点从点出发，沿线段以1单位长度/秒的速度运动，当点与点重合时，整个运动停止．以为一边向上作正方形，若设运动时间为秒，正方形与重合部分的面积为，则下列能大致反映与的函数关系的图象是（ ）

A． B． C． D．
【变式训练】
1．（2023·全国·九年级专题练习）如图，在正方形中，，动点M，N分别从点A，B同时出发，沿射线，射线的方向匀速运动，且速度的大小相等，连接，，．设点M运动的路程为，的面积为，下列图像中能反映与之间函数关系的是（ ）

A． B． C． D．
2．（2023·安徽合肥·校考三模）如图，正方形中，，动点分别从同时出发，点以每秒的速度沿运动，点以每秒的速度沿运动，点到达点时运动停止．设点运动（秒）时，的面积，则关于的函数图象大致为：（ ）

A． B． C． D．
3．（2023·河南南阳·统考一模）如图，在矩形中，，动点P从A点出发，以的速度沿的方向运动，动点Q同时从A点出发，以的速度沿的方向运动，两动点到达C点停止运动．设运动的时间为，的面积为，则下列y关于x的函数图像正确的是（ ）

A． B．C． D．