深圳明德实验学校2023-2024学年八年级上学期期末考试数学试卷(含解析)

这是一份深圳明德实验学校2023-2024学年八年级上学期期末考试数学试卷(含解析)，共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
明德实验学校2023-2024期末数学试卷
一、选择题（每小题只有一个选项符合要求，请在答卷指定区域用2B铅笔填涂所对应的方框，每小题3分，共30分）
1．下列各数，是无理数的是（ ）
A．B．C．D．
2．下列运算正确的是（ ）
A．B．C．D．
3．以下列数据为长度的线段中，可以构成直角三角形的是（ ）
A．1，，B．，3，5C．1，2，3D．2，3，4
4．直线y＝﹣ax+a与直线y＝ax在同一坐标系中的大致图象可能是（ ）
A．B．
C．D．
5．已知，是关于x的函数图象上的两点，当时，，则m的取值范围是（ ）
A．B．C．D．
6．已知方程组的解满足，则k的值是（ ）
A．B．2C．D．
7．《孙子算经》中有一道题，原文是：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余l尺，问木长多少尺？若设木长尺，绳子长尺，则可列方程组为（ ）
A．B．C．D．
8．如下图，在中，，平分，交于点，已知，则的度数为（ ）
A．B．C．D．
9．甲无人机从地面起飞，乙无人机从距离地面20高的楼顶起飞，两架无人机同时匀速上升10s．甲、乙两架无人机所在的位置距离地面的高度y（单位：）与无人机上升的时间x（单位：s）之间的关系如图所示，时，两架无人机的高度差为（ ）
A．10B．15C．20D．25
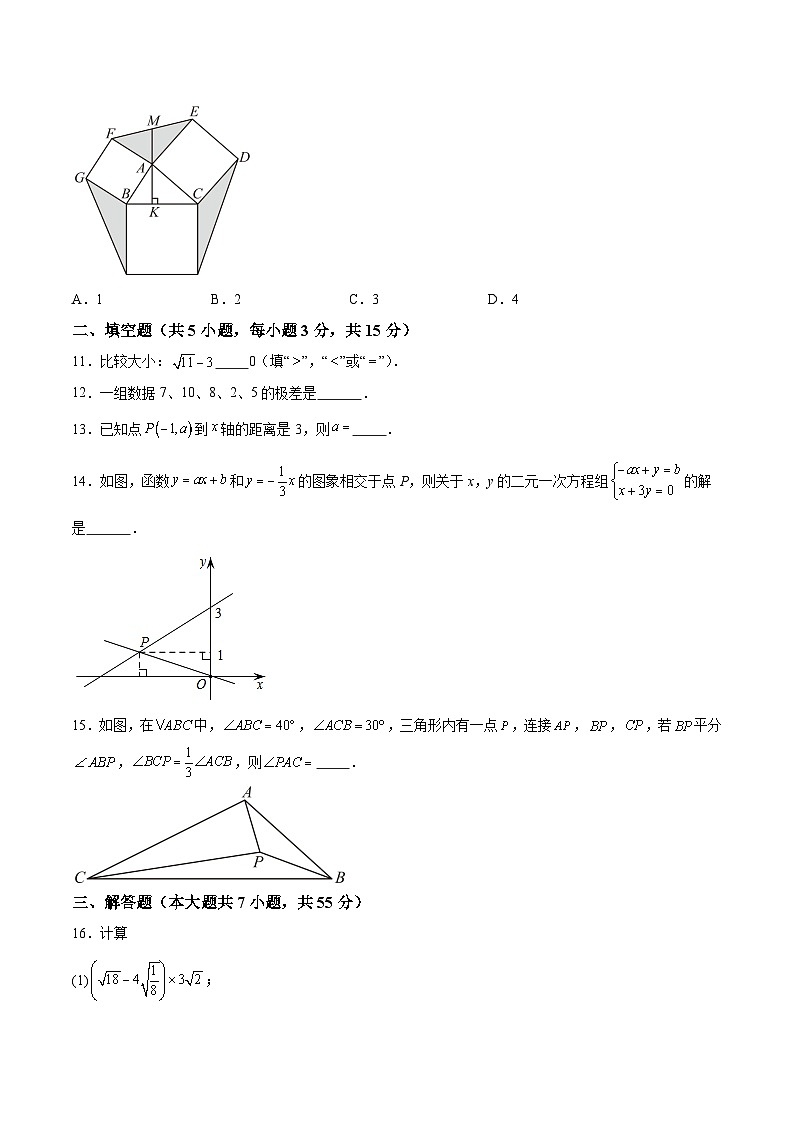
10．如图，分别以的三边，，为边向外侧作正方形，正方形，正方形，连接，，，再过作于，延长交于点．①；②；③；④当，，时，．其中正确的结论共有（ ）个
A．1B．2C．3D．4
二、填空题（共5小题，每小题3分，共15分）
11．比较大小： 0（填“”，“”或“”）．
12．一组数据7、10、8、2、5的极差是 ．
13．已知点到轴的距离是3，则 ．
14．如图，函数和的图象相交于点P，则关于x，y的二元一次方程组的解是 ．
15．如图，在中，，，三角形内有一点，连接，，，若平分，，则 ．

三、解答题（本大题共7小题，共55分）
16．计算
(1)；
(2)．
17．解方程组：．
18．如图，方格纸中的每个小正方形的边长均为1，点和点在小正方形的顶点上．

(1)在网格中建立平面直角坐标系，使A点坐标为，B点坐标为；
(2)在第二象限的格点上找一点C，使为等腰三角形，画出三角形，并写出点C的坐标．
(3)画出关于y轴对称的三角形．
19．为了了解我市八年级学生参加社会实践活动情况，随机抽查了我市某县部分八年级学生第一学期参加社会实践活动的天数，并用得到的数据绘制了两幅统计图，下面给出了两幅不完整的统计图（如图），请根据图中提供的信息，回答下列问题：

(1)______，该扇形所对圆心角的度数为______，请补全条形图．
(2)在这次抽样调查中，众数和中位数分别是多少？
(3)如果该县共有八年级学生16000人，请你估计“活动时间不少于7天”的学生人数大约有多少人？
20．如图，已知点在直线上，点在线段上，与交于点．

(1)求证：；
(2)若，求的度数．
21．2023年夏天，成都将举办第31届世界大学生夏季运动会，成都掀起了一股热爱体育的热潮，为响应积极锻炼的同学们，西川中学计划同时购进一批篮球和排球，若购进2个篮球和1个排球，共需要资金280元；若购进3个篮球和2个排球，共需要资金460元．
(1)求篮球和排球的价格分别为多少元？
(2)学校计划购进两种球类共20个，商场售出一个篮球，利润率为25%，一个排球的进价为50元，为了促销，商场决定每售出一个排球，返还现金m元，而篮球售价不变，要使商场所有购买方案获利相同，求m的值．
22．如图，在平面直角坐标系中，直线与坐标轴相交于点，，点是轴上一点．
(1)求直线的表达式．
(2)如图1，连接，将沿翻折至，若点恰好落在直线上，求点的坐标．
(3)如图2，点在轴的正半轴上，连接，将绕点顺时针旋转至的位置，连接，请问有最小值吗？如果有，请求出来；如果没有，请说明理由．
参考答案
1．C
【详解】解：是分数，是有理数，
是整数，是有理数，
是分数，是有理数，
，是无限不循环小数，是无理数，
故选C
2．D
【详解】解：，故A不符合题意；
，故B不符合题意；
没有意义，故C不符合题意；
，故D符合题意；
故选D
3．A
【详解】解：A、∵，
∴三边长为1，，，可以组成直角三角形，故此选项符合题意；
B、∵，
∴三边长为，3，5，不可以组成直角三角形，故此选项不符合题意；
C、∵，
∴三边长为1，2，3，不可以组成直角三角形，故此选项不符合题意；
D、∵，
∴三边长为2，3，4，不可以组成直角三角形，故此选项不符合题意；
故选：A．
4．D
【详解】解：A、y=ax过第一、三象限，则a＞0，所以y=-ax+a过第一、二、四象限，所以A选项不符合题意；
B、y=ax过第一、三象限，则a＞0，所以y=-ax+a过第一、二、四象限，所以B选项不符合题意；
C、y=ax过第二、四象限，则a＜0，-a＞0，所以y=-ax+a过第一、三、四象限，与y轴的交点在y轴负半轴，所以C选项不符合题意；
D、y=ax过第二、四象限，则a＜0，-a＞0，所以y=-ax+a过第一、三、四象限，与y轴的交点在y轴负半轴，所以D选项符合题意；
故选D．
5．C
【详解】解：当时，，
随的增大而增大，
，
解得：，
的取值范围是．
故选：C．
6．B
【详解】解：，
得，
∵，
∴，
解得，
故选：B．
7．C
【详解】解：设木长尺，绳子长尺，
∵用一根绳子去量一根长木，绳子还剩余4.5尺，
∴．
∵将绳子对折再量长木，长木还剩余l尺，
∴，
∴可列方程组为．
故选C．
8．B
【详解】解：，，
，
平分，
，
，
，
故选：B．
9．C
【详解】由图可得，
甲无人机的速度为
乙无人机的速度为，
∴时，甲无人机所在的位置距离地面的高度为米，
乙无人机所在的位置距离地面的高度，
∴时，两架无人机的高度差为，
故选：C．
10．B
【详解】解：∵，
∴只有满足时，，
又∵并不能得到，
∴不能得到，即不能得到，故①错误；
如图所示，过点F作于Q，过点E作交延长线于Q，
∴，
∴，
∴，
又∵，
∴，
∴，，
同理可得，，
∴，
又∵，
∴，
∴，，故②正确；
∵，
∴，故③正确；
∵，
∴，
同理可得，
∴，
同理可得，
∴，
∵，，，
∴，
∴，故④错误；
故选B．
11．
【详解】解：，
，即，
，
故答案为：．
12．8
【详解】这组数据的最大值为10，最小值为2，
所以这组数据的极差为：，
故答案为：8．
13．
【详解】∵点到轴的距离是3，
∴，
∴，
故答案为：．
14．
【详解】当时，，解得，则点P的坐标为，
所以关于x，y的二元一次方程组中的解为．
故答案为：．
15．##度
【详解】解：如图所示，延长到H使得，连接，
∵，，
∴，
∵，
∴，
∴，
∴，
∵平分，
∴，
又∵，
∴ ，
∴，
∵，
∴，，
∴是等边三角形，
∴，
∴，
∴，
故答案为：．

16．(1)12
(2)
【详解】（1）
；
（2）
．
17．
【详解】解：
，得
，得，
把代入①得，
解得：，
∴原方程组的解是．
18．【详解】（1）解：如图所示；

（2）如图，即为所求；
其中；
（3）如图，即为所求．
19．(1)；；见解析
(2)众数和中位数分别是5天，6天
(3)“活动时间不少于7天”的学生人数大约有6400人
【详解】（1）解：，
该扇形所对圆心角的度数为：，
参加社会实践活动8天的人数为：，
补全的条形统计图如图所示；

（2）解：由条形统计图可知，在这次抽样调查中，参加社会实践活动为5天的人数最多，因此众数是5天，将参加社会实践天数从小到大进行排序，排在中间位置的天数为6天；
（3）解：（人），
答：“活动时间不少于7天”的学生人数大约有6400人．
20．(1)见解析
(2)
【详解】（1）证明：∵
∴
∴
∵
∵
∴
（2）解∵，
∴,
∵,
∴,
∴，
∴
21．(1)篮球的价格为元，排球的价格为元
(2)
【详解】（1）解：设篮球的价格为元，排球的价格为元，由题意，得：
，解得：，
答：篮球的价格为元，排球的价格为元；
（2）设购进篮球个，则购进排球个，设总利润为元，由题意，得：，
整理，得：，
∵商场所有购买方案获利相同，
∴的值与无关，
∴，
∴．
22．(1)
(2)
(3)有最小值，最小值为
【详解】（1）设直线的表达式为，
把，代入可得
，
解得，
∴直线的表达式为；
（2）∵，，
∴，，
∴，，
∵将沿翻折至，
∴，
∴，
∴，
在中，，
∴，
解得,
∴；
（3）过作于，过作于，过作于，
∵
∴设解析式为，
∴设，，，
∴，
∵将绕点顺时针旋转至的位置，
∴，，
∵，
∴，
∴，
∵，，
∴，，
∴，
∴，，
∴，
∵，
∴，
整理得：
∴，解得
∴
∵
∴令，整理得
∴在直线上移动，
∴直线与轴交点坐标，与轴交点坐标，
∴，
∴，
过作于，则即为的最小值，
∴，
∴．
∴有最小值，最小值为．