人教版（2024）七年级下册（2024）7.2.3 平行线的性质教案配套ppt课件

这是一份人教版（2024）七年级下册（2024）7.2.3 平行线的性质教案配套ppt课件，共15页。PPT课件主要包含了学习目标，新知探究，课堂导入，课堂小结，CONTENTS，随堂练习，两直线平行等内容，欢迎下载使用。
1.能够区别平行线的性质与判定；2.能熟练运用平行线的性质与判定解决几何问题.
同位角相等或内错角相等或同旁内角互补
复习 你知道平行线的判定和性质吗？
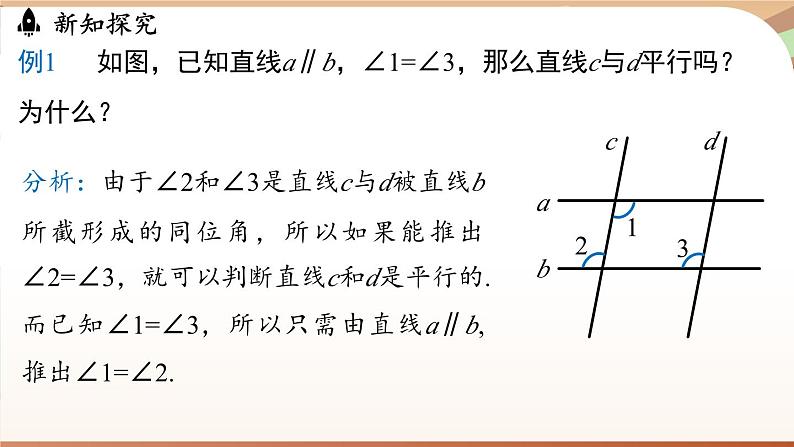
分析：由于∠2和∠3是直线c与d被直线b所截形成的同位角，所以如果能推出∠2=∠3，就可以判断直线c和d是平行的.而已知∠1=∠3，所以只需由直线a∥b,推出∠1=∠2.
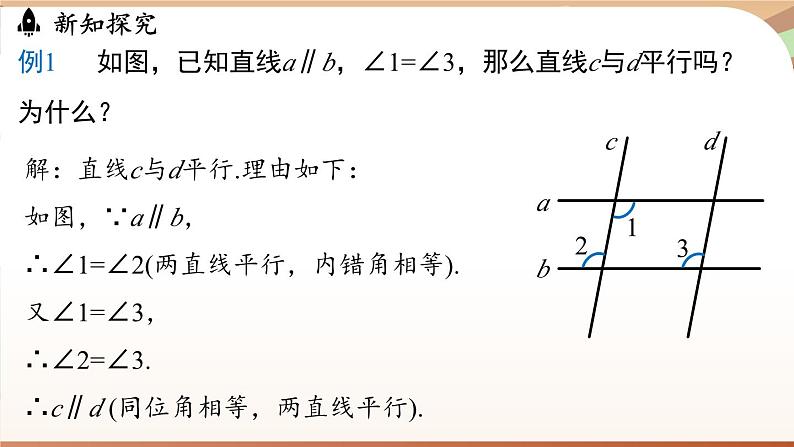
例1如图，已知直线a∥b，∠1=∠3，那么直线c与d平行吗？为什么？
解：直线c与d平行.理由如下：如图，∵a∥b，∴∠1=∠2(两直线平行，内错角相等).又∠1=∠3，∴∠2=∠3.∴c∥d (同位角相等，两直线平行).
例2如图，∠1=∠2，∠3=50°，∠ABC等于多少度？
分析：由于∠3的大小是已知的，所以可以尝试推导∠ABC与∠3的大小关系.而由已知条件∠1=∠2，可以推出a∥b，从而可以得到∠ABC=∠3.
解：∵∠1=∠2，∴a∥b (内错角相等，两直线平行).∴∠3=∠ABC (两直线平行，同位角相等).又∠3=50°，∴∠ABC=50°.
跟踪训练如图，∠1=80°，∠2=100°，且AC∥DF，探索∠C与∠D的数量关系并说明理由．
解：∠C=∠D，理由如下：∵∠1=80°，∠2=100°，∴∠1+∠2=180°，∴BD∥CE，∴∠CEF=∠D，又∵AC∥DF，∴∠CEF=∠C，∴∠C=∠D．
1.如图，AE∥BD，∠A=∠BDC，∠AEC的平分线交CD的延长线于点F．那么AB与CD平行吗？
解：∵AE∥BD，∴∠A+∠ABD=180°.∵∠A=∠BDC，∴∠BDC+∠ABD=180°，∴AB∥CD.
2.国家倡导绿色出行, 数数的爸爸给他买了一辆单车.图 (1)是该品牌单车放在水平地面的实物图, 图 (2)是其示意图, 其中AB,CD都与地面l平行,∠BCD=60°,∠BAC=55°,当∠MAC为多少时, AM∥CB.
解：∵AB,CD都与地面l平行，∴AB∥CD(平行线的基本事实I的推论),∴ ∠BAC+∠ACD=180 °(两直线平行，同旁内角互补)，即∠BAC+∠ACB+∠BCD=180°.∵ ∠BCD=60°， ∠BAC=55°，∴ ∠ACB=65°，∴当∠MAC=∠ACB=65 °时，AM∥CB(内错角相等，两直线平行).
3.如图，AE⊥BC，FG⊥BC，垂足分别是M，N，且∠1=∠2．（1）AB与CD平行吗？
解：（1）平行.理由：∵AE⊥BC，FG⊥BC，∴∠AMC=∠GNC=90°，∴AE∥GF，∴∠1=∠A，∵∠1=∠2，∴∠A=∠2，∴AB∥CD.
3.如图，AE⊥BC，FG⊥BC，垂足分别是M，N，且∠1=∠2．（2）若∠CBD=70°，∠D-∠3=56°，求∠C的度数．
解：∵AB∥CD，∴∠D+∠ABD=180°.∵∠CBD=70°，∠ABD=∠CBD+∠3，∴70°+∠3+∠D=180°.∵∠D-∠3=56°，∴∠D=∠3+56°，∴70°+∠3+∠3+56°=180°，∴∠3=27°.∵AB∥CD，∴∠C=∠3=27°．