安徽省六安市金安区2024-2025学年九年级上学期11月期中考试数学试题（原卷版）-A4

这是一份安徽省六安市金安区2024-2025学年九年级上学期11月期中考试数学试题（原卷版）-A4，共7页。
注意事项：
1．你拿到的试卷满分150分，考试时间为120分钟．
2．本试卷包括“试题卷”和“答题卷”两部分．“试题卷”共4页，“答题卷”共6页．
3．请务必在“答题卷”上答题，在“试题卷”上答题是无效的．
4．考试结束后，请将“试题卷”和“答题卷”一并交回．
一、选择题（本大题共10小题，每小题4分，满分40分）每小题都给出A、B、C、D四个选项，其中只有一个是正确的．
1. 若，则等于（ ）
A. B. C. D.
2. 当时，下列函数中，随的增大而增大的是（ ）
A. B.
C. D.
3. 已知点P是线段AB的黄金分割点，AP＞PB．若AB＝2，则AP的长为（ ）
A. B. 3﹣C. ﹣1D. ﹣3
4. 抛物线与轴只有一个公共点，则的值为（ ）
A. B. C. D. 4
5. 如图，桥梁的两条钢缆具有相同的抛物线形状，而且左、右两条抛物线关于y轴对称，按照图中的直角坐标系左面抛物线可以用表示，则右面抛物线的表达式是（ ）

A. B. C. D.
6. 在如图所示的平面直角坐标系中，与是以为位似中心的位似图形，已知点的坐标为，点的坐标为，则与的周长比是（ ）
A. B. C. D.
7. 已知反比例函数图像上三点、、，则、、的大小关系是（ ）
A. B. C. D.
8. 如图，已知，，，．将沿图中的DE剪开，剪下的阴影三角形与不相似的是（ ）
A. B. C. D.
9. 如图，正方形ABCD由四个全等的直角三角形拼接而成，连结HF交DE于点M．若，则的值为（ ）
A B. C. D.
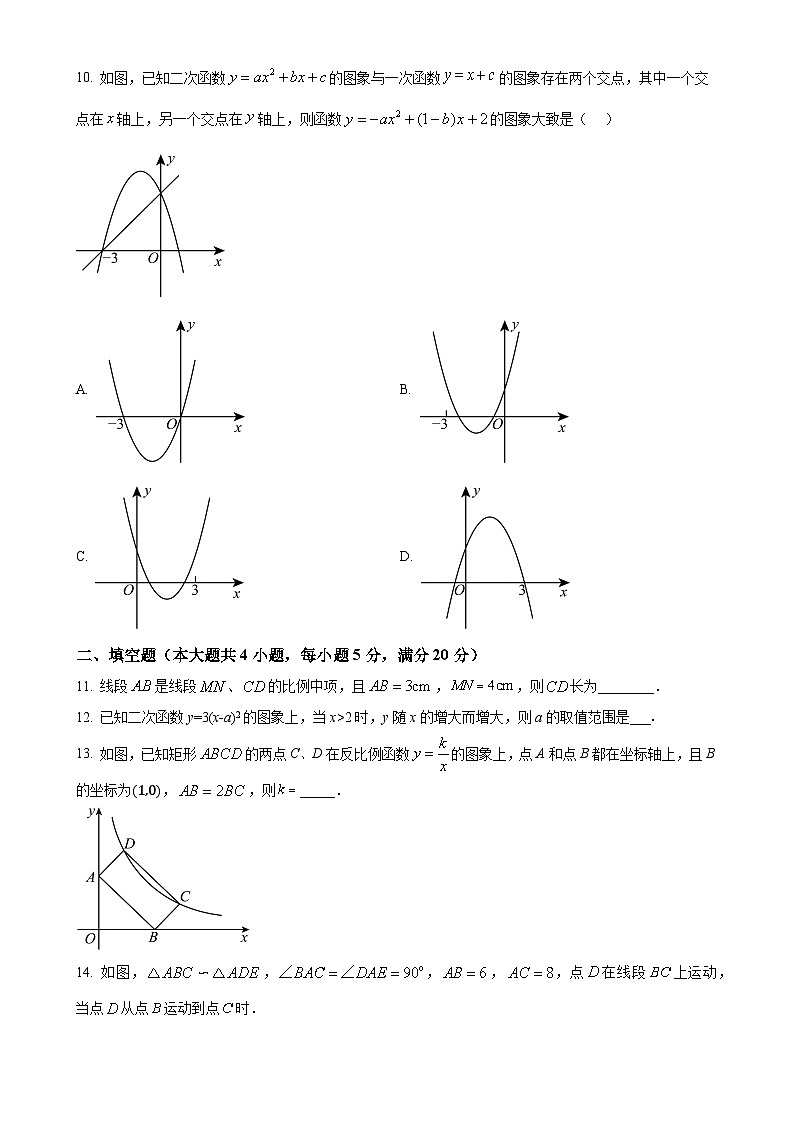
10. 如图，已知二次函数的图象与一次函数的图象存在两个交点，其中一个交点在轴上，另一个交点在轴上，则函数的图象大致是（ ）
A. B.
C. D.
二、填空题（本大题共4小题，每小题5分，满分20分）
11. 线段是线段、的比例中项，且，，则长为________．
12. 已知二次函数y=3(x-a)2的图象上，当x>2时，y随x的增大而增大，则a的取值范围是___．
13. 如图，已知矩形的两点C、D在反比例函数的图象上，点A和点B都在坐标轴上，且B的坐标为1,0，，则_____．
14. 如图，，，，，点在线段上运动，当点从点运动到点时．
（1）当时，则______；
（2）设为线段的中点，在点的运动过程中，的最小值是______．
三、解答题（本大题共2小题，每小题8分，满分16分）
15. 如图是二次函数的图象，其中．试求该抛物线的解析式．
16. 如图，在中，，D为边上一点，且，过点D作．交于点E．求证：．
四、解答题（本大题共2小题，每小题8分，满分16分）
17. 已知汽车匀速从A市行驶到B市，设汽车行驶的时间为t小时，速度为v千米/时，且A市到B市汽车的行驶里程为480千米．
（1）求v关于t的函数表达式（不要求写自变量t的取值范围）；
（2）若汽车从上午从A市出发，如果汽车在当天到之间（包含端点时间）到达B市，求汽车行驶速度v的范围．
18. 如图，在平面直角坐标系中，的顶点坐标分别为O0,0，，．
（1）以原点为位似中心，在轴的右侧画出的位似，使它与的位似比为；
（2）画出将向左平移2个单位，再向上平移1个单位后得到的；
（3）判断和是位似图形吗？若是，请在图中标出位似中心点．
五、解答题（本大题共2小题，每小题10分，满分20分）
19. 规定：在平面直角坐标系中，横、纵坐标互为相反数的点为“完美点”，顶点是“完美点”的二次函数为“完美函数”．
（1）若点是“完美点”，则_____；
（2）已知某“完美函数”的顶点在直线上，且与轴的交点到原点的距离为2，求该“完美函数”的表达式．
20. 在中，，是边上的中线，点D在射线上．
（1）如图1，点D在边上，，与相交于点P，过点A作，交的延长线于点F，易得的值为 ．
（2）如图2，在中，，点D在的延长线上，与边上的中线的延长线交于点P，，求的值：
六、解答题（本题满分12分）
21. 如图，直线与双曲线相交于，B两点，与x轴相交于点．
（1）分别求一次函数与反比例函数的解析式；
（2）连接，求面积；
（3）直接写出当时，关于x的不等式的解集．
七、解答题（本题满分12分）
22. 植物园有一块足够大的空地，其中有一堵长为的墙，现准备用的篱笆围成矩形花圃，小俊设计了甲、乙两种方案(如图所示)：方案甲中的长不超过墙长；方案乙中的长大于墙长．
（1）按图甲方案，设的长为，矩形的面积为．
①求与之间函数关系式；
②求矩形的面积的最大值．
（2）甲、乙哪种方案能使围成矩形花圃的面积最大？最大是多少？请说明理由．
八、解答题（本题满分14分）
23. 如图①，在锐角中，D，E分别是、的中点，点F在上，，交于点M．
（1）求证：；
（2）点G在上，且，如图②，求证：；
（3）在图②中，（2）的基础上，取上一点H，使，若，求的长．