2023-2024学年安徽省六安市金安区九年级（上）期末数学试卷

这是一份2023-2024学年安徽省六安市金安区九年级（上）期末数学试卷，共29页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。
1．下列函数中，的值随值的增大而减小的是
A．B．C．D．
2．如果反比例函数的图象经过点，那么的值是
A．B．C．D．2
3．已知点，，都在反比例函数的图象上，则，，的大小关系为
A．B．C．D．
4．大自然巧夺天工，一片小树叶也蕴含着“黄金分割”，如图，为的黄金分割点，如果的长度为，那么的长度是
A．B．C．D．
5．如图，中，是中线，，，则线段的长为
A．4B．C．6D．
6．阿基米德说：“给我一个支点，我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识——杠杆原理，即“阻力阻力臂动力动力臂”．若已知某一杠杆的阻力和阻力臂分别为和，则这一杠杆的动力和动力臂之间的函数图象大致是
A．B．
C．D．
7．正方形网格中，如图放置，则的值为
A．B．C．1D．
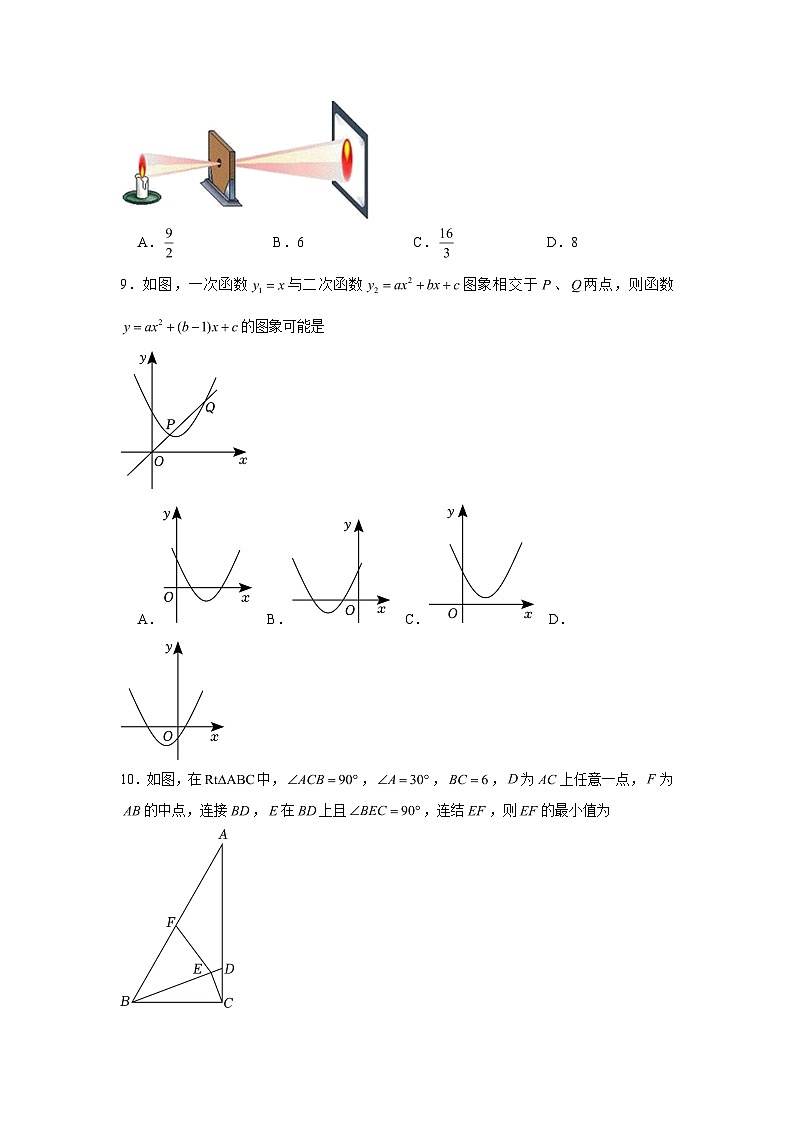
8．大约在两千四五百年前，墨子和他的学生做了世界上第1个小孔成倒像的实验．并在《墨经》中有这样的精彩记录：“景到，在午有端，与景长，说在端”．如图所示的小孔成像实验中，若物距为，像距为，蜡烛火焰倒立的像的高度是，则蜡烛火焰的高度是 ．
A．B．6C．D．8
9．如图，一次函数与二次函数图象相交于、两点，则函数的图象可能是
A． B． C． D．
10．如图，在中，，，，为上任意一点，为的中点，连接，在上且，连结，则的最小值为
A．B．C．D．3
二、填空题（本大题共4小题，每小题5分，共20分）
11．若，则的值为 ．
12．若抛物线与轴只有一个公共点，则的值为 ．
13．（5分）如图，，，，则 ．
14．（5分）如图，点在直线上，轴于点，点在线段上，以为边作正方形，点恰好在反比例函数为常数，第一象限的图象上，连接．
（1）若，，则 ；
（2）若，则 ．
三、（本大题共2小题，每小题8分，共16分）
15．（8分）计算：．
16．（8分）定义新运算：对于任意实数、都有．
例如：，根据以上知识解决下列问题：
求抛物线的顶点坐标．
四、（本大题共2小题，每小题8分，共16分）
17．（8分）如图，在中，，，，求的长．
18．（8分）如图，在边长为1个单位长度的小正方形组成的网格中，按要求画出△和△；
（1）把先向右平移4个单位，再向上平移1个单位，得到△；
（2）以图中的为位似中心，将△作位似变换且放大到原来的两倍，得到△．
五、（本大题共2小题，每小题10分，共20分）
19．（10分）学生到工厂劳动实践，学习制作机械零件．零件的截面如图阴影部分所示，已知四边形为矩形，点、分别在、上，，，，．求零件的截面面积．参考数据：，．
20．（10分）如图，将矩形纸片沿着过点的直线折叠，使点落在边上，落点为，折痕交边于点．
（1）求证：；
（2）若，，求的长；
六、（本大题共2小题，每小题12分，共24分）
21．（12分）如图，一次函数的图象分别与反比例函数的图象在第一象限交于点，与轴的负半轴交于点，且．
（1）求函数和的表达式；
（2）已知点，试在该一次函数图象上确定一点，使得，求此时点的坐标．
22．（12分）在中，，，，现有动点从点出发，沿向点方向运动，动点从点出发，沿线段也向点方向运动，如果点的速度是，点的速度是，它们同时出发，当有一点到达所在线段的端点时，就停止运动．设运动时间为秒．求：
（1）当时，这时，，两点之间的距离是多少？
（2）若的面积为，求关于的函数关系式．
（3）当为多少时，以点，，为顶点的三角形与相似？
七、（本大题共1小题，共14分）
23．（14分）如图，已知抛物线与轴交于点，两点，与轴交于点，点是上方抛物线上的一动点，作轴于点，点的横坐标为，交于点．
（1）求，的坐标和直线的解析式；
（2）连接，求面积的最大值；
（3）已知点也在抛物线上，点的横坐标为，作轴于点，交于点，若，，，为顶点的四边形为平行四边形，求的值．
2023-2024学年九年级（上）期末数学试卷
参考答案与试题解析
一、选择题（本大题共10小题，每小题4分，共40分）
1．（4分）下列函数中，的值随值的增大而减小的是
A．B．C．D．
【答案】
【分析】根据各函数解析式可得随的增大而减小时的取值范围．
【解答】解：选项中，函数，时，随的增大而减小；故不符合题意；
选项中，函数，时，随的增大而减小；故不符合题意；
选项中，函数，随的增大而增大；故不符合题意；
选项中，函数，随的增大而减小．故符合题意；
故选：．
【点评】本题考查二次函数，一次函数的性质，解题关键是掌握二次函数，一次函数图象与系数的关系．
2．（4分）（2008•安徽）如果反比例函数的图象经过点，那么的值是
A．B．C．D．2
【答案】
【分析】把已知点的坐标代入可求出值，即得到反比例函数的解析式．
【解答】解：由题意得：的图象经过点，则，
解得：．
故选：．
【点评】用待定系数法确定反比例函数的比例系数，求出函数解析式．
3．（4分）（2023•济南）已知点，，都在反比例函数的图象上，则，，的大小关系为
A．B．C．D．
【答案】
【分析】首先根据得函数图象的两个分支分别在第二、四象限内，且在每一个象限内随的增大而增大，然后根据点，，的横坐标得，点，在第二象限内，点在第四象限内，进而可判定，，，最后再根据得，据此即可得出答案．
【解答】解：，，
函数图象的两个分支分别在第二、四象限内，且在每一个象限内随的增大而增大，
又点，，，
点，在第二象限内，点在第四象限内，
，，，
又，
，
．
故选：．
【点评】此题主要考查了反比例函数的性质，解答此题的关键是熟练掌握：对于反比例函数，当时，图象的两个分支在第一、三象限内变化，且在每一个象限内随的增大而减小；当时，图象的两个分支在第二、四象限内变化，且在每一个象限内随的增大而增大．
4．（4分）（2023秋•金安区期末）大自然巧夺天工，一片小树叶也蕴含着“黄金分割”，如图，为的黄金分割点，如果的长度为，那么的长度是
A．B．C．D．
【答案】
【分析】由黄金分割知：，由此可求得的长．
【解答】解：为的黄金分割点，
，
即．
故选：．
【点评】本题考查黄金分割的应用，正确记忆相关知识点是解题关键．
5．（4分）（2016•安徽）如图，中，是中线，，，则线段的长为
A．4B．C．6D．
【答案】
【分析】根据是中线，得出，再根据证出，得出，求出即可．
【解答】解：，
，
在和中，
，，
，
，
，
；
故选：．
【点评】此题考查了相似三角形的判定与性质，关键是根据证出，是一道基础题．
6．（4分）（2023•湘潭县三模）阿基米德说：“给我一个支点，我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识——杠杆原理，即“阻力阻力臂动力动力臂”．若已知某一杠杆的阻力和阻力臂分别为和，则这一杠杆的动力和动力臂之间的函数图象大致是
A．B．
C．D．
【答案】
【分析】直接利用阻力阻力臂动力动力臂，进而得出动力关于动力臂的函数关系式，从而确定其图象即可．
【解答】解：阻力阻力臂动力动力臂，且阻力和阻力臂分别为和，
动力关于动力臂的函数解析式为：，
即，是反比例函数，
又动力臂，
故选项符合题意．
故选：．
【点评】本题考查了反比例函数的应用，正确读懂题意得出关系式是解本题的关键．
7．（4分）（2023秋•金安区期末）正方形网格中，如图放置，则的值为
A．B．C．1D．
【答案】
【分析】连接，根据勾股定理可以得到，则是等腰三角形底边上的中线，根据三线合一定理，可以得到是直角三角形．根据三角函数的定义就可以求解．
【解答】解：如图，连接，，设正方形的网格边长是1，则根据勾股定理可以得到：
，，
在中，由等腰三角形三线合一得：，
则，
，
故选：．
【点评】本题考查锐角三角函数的概念，注意到图中的等腰三角形是解决本题的关键．
8．（4分）（2023•白银二模）大约在两千四五百年前，墨子和他的学生做了世界上第1个小孔成倒像的实验．并在《墨经》中有这样的精彩记录：“景到，在午有端，与景长，说在端”．如图所示的小孔成像实验中，若物距为，像距为，蜡烛火焰倒立的像的高度是，则蜡烛火焰的高度是 ．
A．B．6C．D．8
【答案】
【分析】过点作，垂足为，延长交于点，根据题意可得：，，，，然后利用平行线的性质可得：，从而可得，然后利用相似三角形的性质进行计算，即可解答．
【解答】解：如图：过点作，垂足为，延长交于点，
由题意得：
，，，
，
，
，
，，
，
，
，
解得：，
蜡烛火焰的高度是，
故选：．
【点评】本题考查了相似三角形的应用，熟练掌握相似三角形的判定与性质是解题的关键．
9．（4分）（2023•包头模拟）如图，一次函数与二次函数图象相交于、两点，则函数的图象可能是
A．B．
C．D．
【答案】
【分析】由一次函数与二次函数图象相交于第一象限的、两点，得出函数与轴有两个交点，两个交点在轴的正半轴，即可进行判断．
【解答】解：由图象可知一次函数与二次函数交于第一象限的、两点，
函数与轴有两个交点，两个交点在轴的正半轴，
符合条件，
故选：．
【点评】本题考查了二次函数的图象，直线和抛物线的交点，交点坐标和方程的关系以及方程和二次函数的关系等，熟练掌握二次函数的性质是解题的关键．
10．（4分）（2023•贵池区二模）如图，在中，，，，为上任意一点，为的中点，连接，在上且，连结，则的最小值为
A．B．C．D．3
【答案】
【分析】根据锐角三角函数得到，再利用中位线定理得到，最后根据、、三点共线的时，的值最小即可解答．
【解答】解：取的中点，连接，，
为的中点，
，
，，，
，
，
，
，
当、、三点共线的时，的值最小，
．
故选：．
【点评】本题考查了锐角三角函数的定义，直角三角形的性质，三角形中位线定理，掌握三角形中位线定理是解题的关键．
二、填空题（本大题共4小题，每小题5分，共20分）
11．（5分）（2023秋•金安区期末）若，则的值为 ．
【分析】将分式化成含有的形式，再代入的值计算即可．
【解答】解：．
【点评】本题考查了分式的求值，将分式转化为含已知值的形式，利用整体代入法是解本题的关键．
12．（5分）（2023•荔湾区一模）若抛物线与轴只有一个公共点，则的值为 9 ．
【分析】根据抛物线与轴只有一个公共点，得出，解出即可．
【解答】解：抛物线与轴只有一个公共点，
，
，
故答案为：9．
【点评】本题考查抛物线与轴只有公共点、二次函数的性质，掌握这两个知识点的综合应用是解题关键．
13．（5分）（2023秋•金安区期末）如图，，，，则 ．
【分析】利用相似三角形的性质求解．
【解答】解：，
，
，
，
，
故答案为：．
【点评】本题考查相似三角形的性质，解题的关键是掌握相似三角形对应边的比相等，都等于相似比．
14．（5分）（2023秋•金安区期末）如图，点在直线上，轴于点，点在线段上，以为边作正方形，点恰好在反比例函数为常数，第一象限的图象上，连接．
（1）若，，则 16 ；
（2）若，则 ．
【分析】（1）根据，可以计算出点的坐标为，进而计算出的值；
（2）设正方形的边长为，，则，，利用等腰直角三角形的性质得，，点在反比例函数的图象上，，可得，再代入计算．
【解答】解：（1）点在直线上，，
，即，
，，
，点的横坐标为：，
点的坐标为：，
．
故答案为：16；
（2）设正方形的边长为，，
则，，
，，
点在反比例函数的图象上，，
，即，
．
故答案为：14．
【点评】本题考查了反比例函数与一次函数的交点问题，正方形的性质，勾股定理，平方差公式，等腰直角三角形的判定和性质，熟知以上知识是解题的关键．
三、（本大题共2小题，每小题8分，共16分）
15．（8分）（2009•安徽）计算：．
【分析】本题涉及绝对值、负整数指数幂、特殊角的三角函数值、二次根式化简四个考点．在计算时，需要针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．
【解答】解：原式．
【点评】本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟记特殊角的三角函数值，熟练掌握负整数指数幂、二次根式、绝对值等考点的运算．
16．（8分）（2023秋•金安区期末）定义新运算：对于任意实数、都有．
例如：，根据以上知识解决下列问题：
求抛物线的顶点坐标．
【答案】．
【分析】利用新定义运算法则列出方程，然后利用配方法写出顶点式解析式，可以直接得到答案．
【解答】解：根据题意知，
，
顶点坐为．
【点评】本题主要考查了解一元二次方程，二次函数的性质，求抛物线的顶点坐标，解题的关键是掌握新定义运算法则．
四、（本大题共2小题，每小题8分，共16分）
17．（8分）（2012•安徽）如图，在中，，，，求的长．
【分析】过作于，求出，推出，根据含30度角的直角三角形求出，根据勾股定理求出，相加即可求出答案．
【解答】解：
过作于，
，
，
，
，
，，
，
，
由勾股定理得：，
，
答：的长是．
【点评】本题考查了勾股定理，等腰三角形的性质和判定，含30度角的直角三角形性质等知识点的应用，关键是构造直角三角形，题目具有一定的代表性，是一道比较好的题目．
18．（8分）（2011•安徽）如图，在边长为1个单位长度的小正方形组成的网格中，按要求画出△和△；
（1）把先向右平移4个单位，再向上平移1个单位，得到△；
（2）以图中的为位似中心，将△作位似变换且放大到原来的两倍，得到△．
【分析】（1）把、、三点先向右平移4个单位，再向上平移1个单位得到，，，顺次连接得到的各点即可；
（2）延长到，使，同法得到其余各点，顺次连接即可．
【解答】解：如图
【点评】本题考查图形的平移变换及位似变换，注意图形的变换，看关键点作变换即可．
五、（本大题共2小题，每小题10分，共20分）
19．（10分）学生到工厂劳动实践，学习制作机械零件．零件的截面如图阴影部分所示，已知四边形为矩形，点、分别在、上，，，，．求零件的截面面积．参考数据：，．
【分析】由四边形为矩形，可得，则，又，结合三角函数值可求出与的长度，又是，在中，结合三角函数值可求出，的长度，由零件的截面面积矩形的面积的面积的面积，即可得出结论．
【解答】解：法一、如图，
四边形为矩形，，
，，
，
在中，，，，
，，
，，
，
，
，
在中，，，
，，
，，
，
，
，
，
截面的面积．
法二、如图，延长交的延长线于点，
，
，
，
，
，
，
，
截面的面积．
【点评】本题主要考查解直角三角形，题目本身不难，但是计算比较复杂，清楚了解每一步如何计算是解题基础．
20．（10分）（2023秋•金安区期末）如图，将矩形纸片沿着过点的直线折叠，使点落在边上，落点为，折痕交边于点．
（1）求证：；
（2）若，，求的长；
【分析】（1）由折叠性质得，再根据互余性质得出和的两个锐角相等，便可由相似三角形的判定得出结论；
（2）由折叠性质得，再由勾股定理求得，由线段和差求得，由勾股定理可求解．
【解答】（1）证明：四边形是矩形，
，
根据折叠性质知，，
，
，
；
（2）解：由折叠性质知，，，
，
，
，
．
，
．
【点评】本题考查了矩形的性质，相似三角形的性质与判定，折叠的性质，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，注意对应相等关系．
六、（本大题共2小题，每小题12分，共24分）
21．（12分）（2020•鄂尔多斯）如图，一次函数的图象分别与反比例函数的图象在第一象限交于点，与轴的负半轴交于点，且．
（1）求函数和的表达式；
（2）已知点，试在该一次函数图象上确定一点，使得，求此时点的坐标．
【分析】（1）利用待定系数法即可解答；
（2）设点的坐标为，根据，得到，即可解答．
【解答】解：（1）把点代入函数得：，
．
，
，
，
点的坐标为，
把，代入得：
解得：
．
（2）方法一：点在一次函数上，
设点的坐标为，
，
解得：，
点的坐标为．方法二：、，
，
的中垂线为：直线，
当时，，即，
点的坐标为．
【点评】本题考查了一次函数与反比例函数的交点，解决本题的关键是利用待定系数法求解析式．
22．（12分）（2021•罗湖区校级模拟）在中，，，，现有动点从点出发，沿向点方向运动，动点从点出发，沿线段也向点方向运动，如果点的速度是，点的速度是，它们同时出发，当有一点到达所在线段的端点时，就停止运动．设运动时间为秒．求：
（1）当时，这时，，两点之间的距离是多少？
（2）若的面积为，求关于的函数关系式．
（3）当为多少时，以点，，为顶点的三角形与相似？
【分析】（1）在中，当，可知、的长，运用勾股定理可将的长求出；
（2）由点，点的运动速度和运动时间，又知，的长，可将、用含的表达式求出，代入直角三角形面积公式求解；
（3）应分两种情况：当时，根据，可将时间求出；当时，根据，可求出时间．
【解答】解：由题意得，，则，
（1）当时，，，
由勾股定理得；
（2）由题意得，，则，
因此的面积为；
（3）分两种情况：
①当时，，即，解得；
②当时，，即，解得．
因此或时，以点、、为顶点的三角形与相似．
【点评】本题主要考查相似三角形性质的运用，在解第三问时应分两种情况进行求解，在解题过程应防止漏解或错解．
七、（本大题共1小题，共14分）
23．（14分）（2023秋•金安区期末）如图，已知抛物线与轴交于点，两点，与轴交于点，点是上方抛物线上的一动点，作轴于点，点的横坐标为，交于点．
（1）求，的坐标和直线的解析式；
（2）连接，求面积的最大值；
（3）已知点也在抛物线上，点的横坐标为，作轴于点，交于点，若，，，为顶点的四边形为平行四边形，求的值．
【分析】（1）令，则，解方程求出的值即可；根据，坐标，用待定系数法求一次函数解析式即可；
（2）根娱点的横坐标为，点在抛物线上，在直线，得出，，从而得出，然后由三角形的面积公式得出，再由函数的性质求最值即可；
（3）分四边形为平行四边形和四边形为平行四边形两种情况，由，的坐标求出，，再根据得出关于的方程，解方程求出即可．
【解答】解：（1）令，则，
解得，，
，；
令，则，
，
设直线的解析式为，
把，代入解析式得：，
解得，
直线的解析式为；
（2）点的横坐标为，点在抛物线上，在直线，
，，
，
，
，
当时，有最大值，最大值为，
面积的最大值为；
（3）①如图所示，当四边形为平行四边形时，
轴，轴，
，
四边形为平行四边形，
，
点的横坐标为，点在抛物线上，在直线，
，，
，
，
解得；
②如图所示，当四边形为平行四边形时，
同①得出，
，
解得，，
，
．
综上所述，或．
【点评】本题考查二次函数的综合题，关键是掌握待定系数法求函数解析式，函数的性质以及平行四边形的性质．