沪教版（五四制）（2024）九年级下册27.3 垂径定理教学课件ppt

这是一份沪教版（五四制）（2024）九年级下册27.3 垂径定理教学课件ppt，共19页。PPT课件主要包含了或2cm，分类讨论思想，又∵ACAB，∴AEAD，解连接OC，根据勾股定理得，解得R545等内容，欢迎下载使用。
学习目标掌握垂径定理及其推论，并会添加常规辅助线.2.在运用垂径定理及推论解决有关数学问题时，感受分类讨论的数学思想.
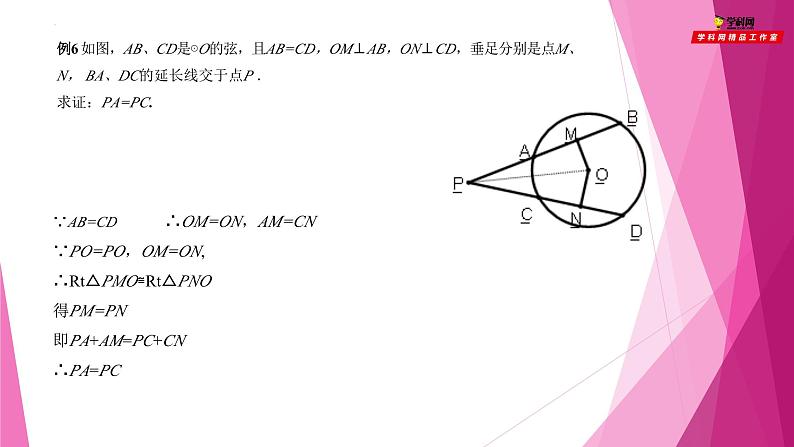
例6 如图，AB、CD是⊙O的弦，且AB=CD，OM⊥AB，ON⊥CD，垂足分别是点M、N， BA、DC的延长线交于点P ． 求证：PA=PC.
∵AB=CD ∴OM=ON，AM=CN∵PO=PO，OM=ON,∴Rt△PMO≌Rt△PNO得PM=PN即PA+AM=PC+CN∴PA=PC
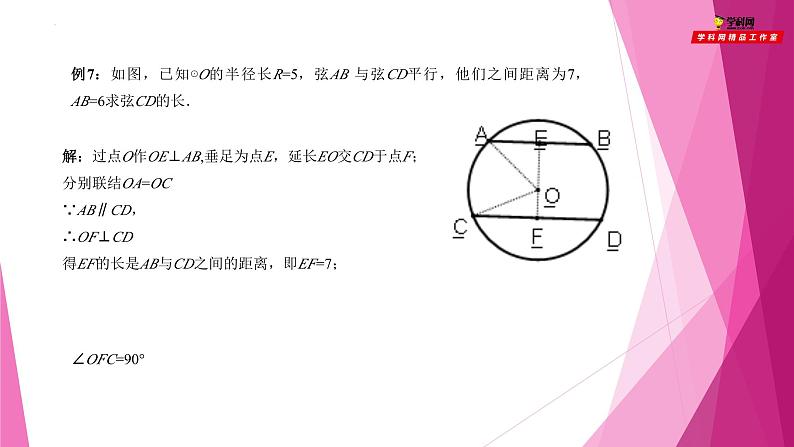
例7：如图，已知⊙O的半径长R=5，弦AB 与弦CD平行，他们之间距离为7，AB=6求弦CD的长．
解：过点O作OE⊥AB,垂足为点E，延长EO交CD于点F；分别联结OA=OC∵AB∥CD，∴OF⊥CD得EF的长是AB与CD之间的距离，即EF=7；
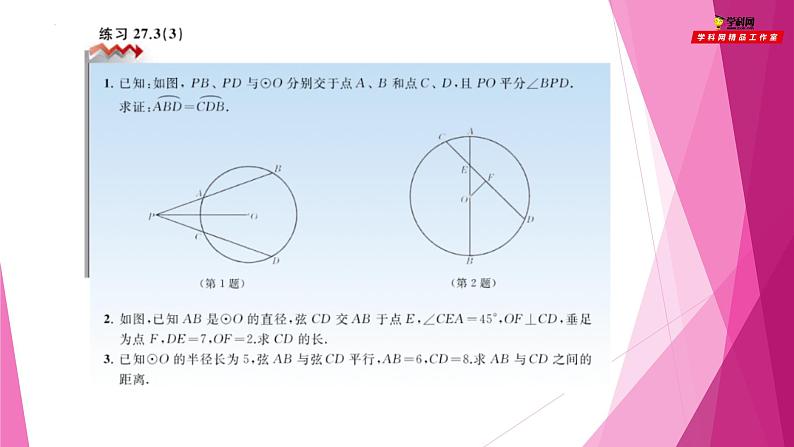
1、如图,AB为⊙O 的直径,E是BC的中点，OE交弦BC于点D.已知BC=10cm,DE=1cm,则半径的长为 .
2、已知⊙O的半径为10cm，弦AB∥CD,且AB=12cm,CD=16cm,则弦AB和CD之间的距离为 .
EF=OE+OF=14cm
EF=OE-OF=2cm
3.如图，在⊙O中，AB、AC为互相垂直且相等的两条弦，OD⊥AB于D，OE⊥AC于E，求证四边形ADOE是正方形．
∴四边形ADOE为矩形，
∴ 四边形ADOE为正方形.
4.已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D两点。你认为AC和BD有什么关系？为什么？
证明：过O作OE⊥AB，垂足为E， 则AE＝BE，CE＝DE. ∴ AE－CE＝BE－DE 即 AC＝BD.
注意：解决有关弦的问题，常过圆心作弦的弦心距，或作垂直于弦的直径，它是一种常用辅助线的添法．
5.如图，一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD，垂足为F,EF=90m.求这段弯路的半径.
设这段弯路的半径为Rm,则OF=(R-90)m.
∴这段弯路的半径约为545m.
6．【中考·湖州】已知在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于点C、D(如图)．
(1)求证：AC＝BD；
证明：如图，过点O作OE⊥AB于点E，则CE＝DE，AE＝BE.∴AE－CE＝BE－DE，即AC＝BD.
7．如图，有两条公路OM、ON相交成30°角，沿公路OM方向离O点80 m处有一所学校A.当重型运输卡车P沿公路ON方向行驶时，在以P为圆心，50 m长为半径的圆形区域内都会受到卡车噪声的影响，且卡车P与学校A的距离越近噪声影响越大．若该重型运输卡车P沿公路ON方向行驶的速度为18 km/h.　
(1)求对学校A的噪声影响最大时卡车P与学校A的距离；
解：如图，过点A作AD⊥ON于点D.∵∠NOM＝30°，AO＝80 m，∴AD＝40 m，即对学校A的噪声影响最大时卡车P与学校A的距离为40 m.