人教版数学七年级下册期末培优专题13 相交线与平行线中的动点问题训练（2份，原卷版+解析版）

这是一份人教版数学七年级下册期末培优专题13 相交线与平行线中的动点问题训练（2份，原卷版+解析版），文件包含人教版数学七年级下册期末培优专题13相交线与平行线中的动点问题训练原卷版doc、人教版数学七年级下册期末培优专题13相交线与平行线中的动点问题训练解析版doc等2份试卷配套教学资源，其中试卷共51页， 欢迎下载使用。
解答题解题策略：（1）常见失分因素：①对题意缺乏正确的理解，应做到慢审题快做题；②公式记忆不牢，考前一定要熟悉公式、定理、性质等；③思维不严谨，不要忽视易错点；④解题步骤不规范，一定要按课本要求，否则会因不规范答题而失分，避免“对而不全”，如解概率题时，要给出适当的文字说明，不能只列几个式子或单纯的结论，表达不规范、字迹不工整等非智力因素会影响阅卷老师的“感情分”；⑤计算能力差导致失分多，会做的试题一定不能放过，不能一味求快，⑥轻易放弃试题，难题不会做时，可分解成小问题，分步解决，如最起码能将文字语言翻译成符号语言、设应用题未知数、设轨迹的动点坐标等，都能拿分。也许随着这些小步骤的罗列，还能悟出解题的灵感。
（2）何为“分段得分”：对于同一道题目，有的人理解的深，有的人理解的浅；有的人解决的多，有的人解决的少。为了区分这种情况，中考的阅卷评分办法是懂多少知识就给多少分。这种方法我们叫它“分段评分”，或者“踩点给分”——踩上知识点就得分，踩得多就多得分。与之对应的“分段得分”的基本精神是，会做的题目力求不失分，部分理解的题目力争多得分。对于会做的题目，要解决“会而不对，对而不全”这个老大难问题。有的考生拿到题目，明明会做，但最终答案却是错的——会而不对。有的考生答案虽然对，但中间有逻辑缺陷或概念错误，或缺少关键步骤——对而不全。因此，会做的题目要特别注意表达的准确、考虑的周密、书写的规范、语言的科学，防止被“分段扣分”。经验表明，对于考生会做的题目，阅卷老师则更注意找其中的合理成分，分段给点分，所以“做不出来的题目得一二分易，做得出来的题目得满分难”。
对绝大多数考生来说，更为重要的是如何从拿不下来的题目中分段得点分。我们说，有什么样的解题策略，就有什么样的得分策略。把你解题的真实过程原原本本写出来，就是“分段得分”的全部秘密。
①缺步解答：如果遇到一个很困难的问题，确实啃不动，一个聪明的解题策略是，将它们分解为一系列的步骤，或者是一个个小问题，先解决问题的一部分，能解决多少就解决多少，能演算几步就写几步，尚未成功不等于失败。特别是那些解题层次明显的题目，或者是已经程序化了的方法，每一步得分点的演算都可以得分，最后结论虽然未得出，但分数却已过半，这叫“大题拿小分”。
②跳步答题：解题过程卡在某一过渡环节上是常见的。这时，我们可以先承认中间结论，往后推，看能否得到结论。如果不能，说明这个途径不对，立即改变方向；如果能得出预期结论，就回过头来，集中力量攻克这一“卡壳处”。由于考试时间的限制，“卡壳处”的攻克如果来不及了，就可以把前面的写下来，再写出“证实某步之后，继续有……”一直做到底。也许，后来中间步骤又想出来，这时不要乱七八糟插上去，可补在后面。若题目有两问，第一问想不出来，可把第一问作为“已知”，先做第二问，这也是跳步解答。
③退步解答：“以退求进”是一个重要的解题策略。如果你不能解决所提出的问题，那么，你可以从一般退到特殊，从抽象退到具体，从复杂退到简单，从整体退到部分，从较强的结论退到较弱的结论。总之，退到一个你能够解决的问题。为了不产生“以偏概全”的误解，应开门见山写上“本题分几种情况”。这样，还会为寻找正确的、一般性的解法提供有意义的启发。
④辅助解答：一道题目的完整解答，既有主要的实质性的步骤，也有次要的辅助性的步骤。实质性的步骤未找到之前，找辅助性的步骤是明智之举。如：准确作图，把题目中的条件翻译成数学表达式，设应用题的未知数等。答卷中要做到稳扎稳打，字字有据，步步准确，尽量一次成功，提高成功率。试题做完后要认真做好解后检查，看是否有空题，答卷是否准确，所写字母与题中图形上的是否一致，格式是否规范，尤其是要审查字母、符号是否抄错，在确信万无一失后方可交卷。
一、解答题
综合与探究：
将三角形纸板如图放置，点P是边AB边上一点，，，，
探究：
如果，，则______．
猜想：
当点P在E、F两点之间运动时，与、之间有何数量关系？并说明理由；
拓展：
如果点P在E、F两点外侧运动时点P与点A、B、E、F四点不重合，上述中的结论是否还成立？并说明理由．
【答案】
【知识点】三角形综合、平行线的性质
【解析】解：如图1，过P作，
，
，，
，
，
，
故答案为：；
，
理由如下：如图1，过P作，
，
，，
，
，
；
如图2，当点P在FE的延长线上时，，
理由如下：过P作，
，
，，
，
，
；
如图3，当点P在EF的延长线上时，，
理由如下：过P作，
，
，，
，
，
．
过P作，根据平行线的性质得到，根据平行公理得到，得到，结合图形计算，得到答案；
根据的作法解答；
分当点P在FE的延长线上、当点P在EF的延长线上两种情况，根据平行线的性质解答．
本题考查的是平行线的判定和性质，正确作出辅助性、掌握两直线平行、内错角相等是解题的关键．
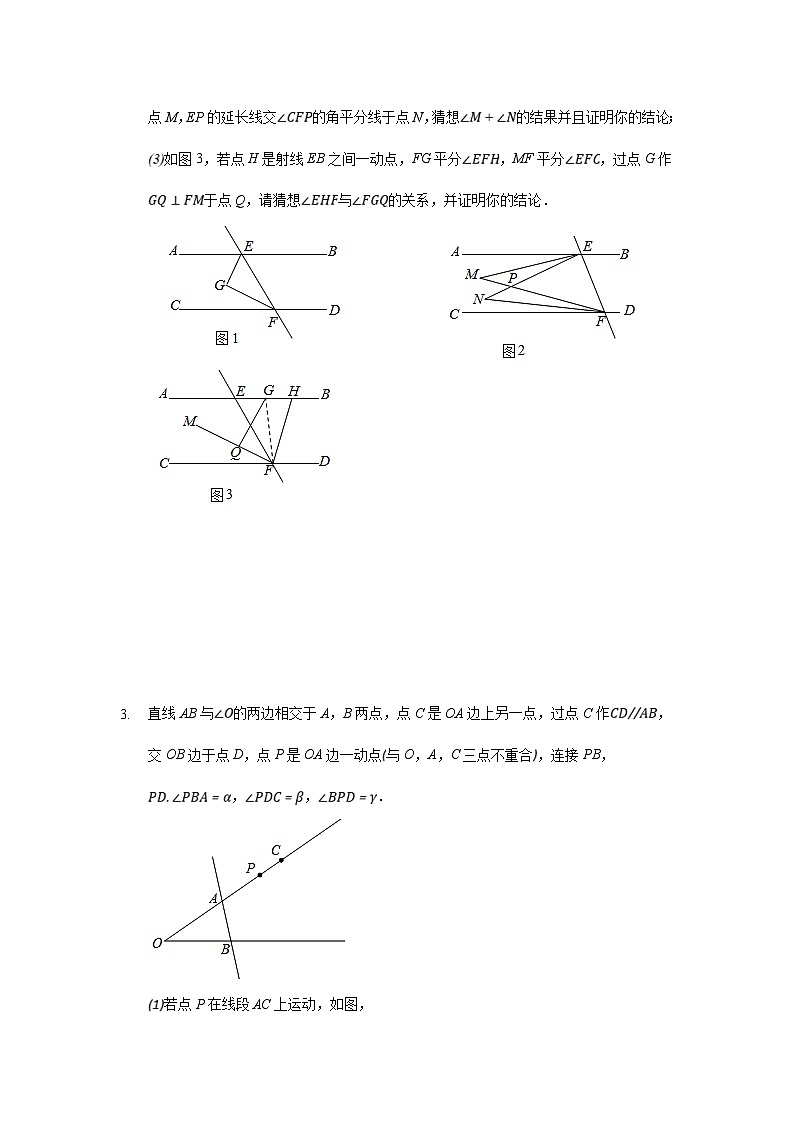
如图1，，G为AB、CD之间一点．
若GE平分，GF平分求证：；
如图2，若，，且FP的延长线交的角平分线于点M，EP的延长线交的角平分线于点N，猜想的结果并且证明你的结论；
如图3，若点H是射线EB之间一动点，FG平分，MF平分，过点G作于点Q，请猜想与的关系，并证明你的结论．
【答案】解：，
，
平分，GF平分，
，，
，
即；
分别过M，N作，，
，
，
，，，，
，，
同理：，
，
平分，FN平分，
，，
，
，，
，
；
．
证明：，
，
，
，
平分，MF平分，
，，
，
．
【知识点】平行线的性质、垂线的相关概念及表示
【解析】根据平行线的性质可得，再利用角平分线的定义可求解，进而证明结论；
分别过M，N作，，根据平行线的性质可得，再根据角平分线的定义结合，，可求解；
根据垂线的定义可求得，再根据角平分线的定义可求解．
本题主要考查平行线的性质，角平分线的定义，垂线的定义，灵活运用平行线的性质及角平分线的定义是解题的关键．
直线AB与的两边相交于A，B两点，点C是OA边上另一点，过点C作，交OB边于点D，点P是OA边一动点与O，A，C三点不重合，连接PB，，，．
若点P在线段AC上运动，如图，
依题意补全图；
判断，，的数量关系并加以证明；
若点P在线段AC外运动时，直接写出，，的数量关系．
【答案】解：依题意补全图形如图1所示；
，，的数量关系为：，
证明：如图2，过点P作，
，，
，
，，
．
即；
如图3，若点P在线段AC的延长线上运动时，；
理由：过点P作，
，，
，
，，
．
即；
如图4，若点P在线段OA上运动时，；
理由：过点P作，
，，
，
，，
，
即．
【知识点】平行公理及推论、角的计算、平行线的性质
【解析】本题主要考查了平行线的性质，角的和差，正确的作出图形是解题的关键．
根据题意补全图形即可；
如图2，过点P作，根据平行线的性质和角的和差即可得到结论；
如图3，若点P在线段AC的延长线上运动时，如图4，若点P在线段OA上运动时，；根据平行线的性质和角的和差即可得到结论．
如图，已知，点P是射线AM上一动点与点A不重合，BC、BD分别平分和，分别交射线AM于点C，D．
求的度数；
当点P运动时，与之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由；若变化，请写出变化规律．
当点P运动到使时，的度数是______．
【答案】，
，
，
，
、BD分别平分和，
，，
；
不变化，，
证明：，
，
，
又平分，
，
；

【知识点】平行线的性质
【解析】
解：见答案
见答案
，
，
又，
，
，
由可得，，，
，
故答案为：．
【分析】
先根据平行线的性质，得出，再根据BC、BD分别平分和，即可得出的度数；
根据平行线的性质得出，，再根据BD平分，即可得到进而得出；
根据，，得出，进而得到，根据，，可求得的度数．
本题主要考查了平行线的性质，角平分线的性质的运用，解决问题的关键是掌握：两直线平行，内错角相等．
已知：直线EF分别与直线AB，CD相交于点G，H，并且．
如图1，求证：；
如图2，点M在直线AB，CD之间，连接GM，HM，求证：；
如图3，在的条件下，射线GH是的平分线，在MH的延长线上取点N，连接GN，若，，求的度数．
【答案】解：证明：如图1，，．
，
；
证明：如图2，过点M作，
又，
．
，．
；
如图3，令，，则，，
射线GH是的平分线，
，
，
，
，
，
过点H作，
则，，
，
，
，
，
，
，
．
【知识点】角的计算、平行线的判定与性质
【解析】本题考查了平行线的判定与性质，角度计算，解决本题的关键是掌握平行线的判定与性质．
根据已知条件和对顶角相等即可证明；
如图2，过点M作，可得进而可以证明；
如图3，令，，则，，过点H作，可得，，进而可得结论．
已知直线，且与，分别交于A，B两点，与，相交于C，D两点，点P在直线AB上运动．
如图1，当点P在A，B两点间运动时，试探究，，之间的关系，并说明理由；
如图2，A点在B处北偏东方向，A点在C处的北偏西方向，应用探究的结论求出的度数；
如果点P在A，B两点外侧运动时，画出图形并直接写出，，之间的关系．
【答案】解：当点P在A、B两点间运动时，保持不变．
理由：过点P作，交CD于点Q，如图所示．
，，
又，，，
，
，
即．
分别在B点和C点处画方位图，如图所示．
由知：，
．
．
分两种情况：
当点P在A点上方时，过点P作，交直线CD于点Q，如图所示．
，．
又，，，
．
又，
；
当点P在B点下方时，过点P作，交CD于点Q，如图4所示．
同理可得：．
综上所述：．
【知识点】方向角、平行线的性质
【解析】本题考查了平行线的性质以及方向角的应用，解题的关键是：根据平行线的性质找出“，”；利用中结论进行计算；需要分情况讨论，解决该题型题目时，利用平行线的性质找出相等或互补的角是关键．
过点P作，交CD于点Q，由结合“两直线平行，内错角相等”找出“，”，再通过角的计算即可得出结论；
分别在B点和C点处画方位图，结合的结论即可得到结果；
分两种情况进行讨论：当点P在A点上方时，过点P作，交CD于点Q，由结合“两直线平行，内错角相等”找出“，”，再通过角的计算即可得出结论；当点P在B点下方时，过点P作，交CD于点Q，利用的方法可得出结论．
如图，，点A为直线MN上一定点，B为直线OP上的动点，在直线MN与OP之间且在线段AB的右方作点D，使得设为锐角．
求与的和；提示过点D作
当点B在直线OP上运动时，试说明；
当点B在直线OP上运动的过程中，若AD平分，AB也恰好平分，请求出此时的值
【答案】解：如图，过点D作，则．
，，
．
，
．
，
，
．
由得：，则．
，
，
．
若AD平分，AB也恰好平分，则有，，．
，
，
．
由知：，则，解得：．
【知识点】平行线的性质、垂线的相关概念及表示
【解析】过点D作，则，，依据平行线的性质可得到，则，最后，依据垂线的定义求解即可；由得，然后结合，进行证明即可；
先求得的度数用含的式子表示，然后再利用中的结论列方程求解即可．
本题主要考查的是平行线的性质和判定，熟练掌握平行线的性质定理是解题的关键．
已知：和同一平面内的点
如图1，若点P在BC边上，过点P作交AC于点E，作交AB于点根据题意，请在图1中补全图形，并直接写出与的数量关系
如图2，若点P在CB的延长线上，且，请判断AB与PE的位置关系，并说明理由
如图3，点P是外部的一点，过点P作交直线AC于点E，作交直线AB于点F，请直接写出与的数量关系，并在图3中补全图形．
图1
图2
图3
【答案】解：如图1中，结论：．
理由：，
，
，
，
．
如图2中，结论：．
理由：延长FP交AB的延长线于点D．
，
，
，
，
．
如图中，结论：．
理由：，
，
，
，
．
如图中，．
理由：，
，
，
，
．
综上所述，：或．
【知识点】平行线的判定与性质
【解析】本题考查平行线的性质等知识，解题的关键是熟练掌握平行线的性质和理解题意，学会用分类讨论的思想思考问题，属于中考常考题型．
结论：理由平行线的性质解决问题即可．
结论：延长FP交AB的延长线于点想办法证明即可．
如图中，结论：理由平行线的性质证明即可．如图中，理由平行线的性质证明即可．
如图，已知直线、，直线和直线、交于点C和D，在直线上有动点点P与点C、D不重合，点A在直线上，点B在直线上．
问题发现：如果点P在C、D之间运动时，且满足，请写出与之间的位置关系______；
拓展探究：如图如果，点P在直线的上方运动时，试猜想与之间关系并给予证明；
问题解决：如果，点P在直线的下方运动时，请直接写出、、之间的关系．
【答案】
如图所示，当点P在线段DC的延长线上时，，
理由是：因为，
所以
因为，
所以；
如图所示，
当点P在直线的下方运动时，．
理由：过点P作，AP交于点Q
．
因为，
所以，
又，
所以，
即．
【知识点】平行线的判定与性质
【解析】
如图，延长BP交AC于E，
因为，，
所以，
所以，
故答案为：；
见答案；
见答案．
【分析】
如图所示，作辅助线，根据平行线的判定可得结论；
如图所示，根据平行线的性质，即可得证；
如图所示，过点P作，同理即可得证．
此题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解本题的关键．
已知：如图1，，C在D的右侧，BE平分，DE平分，BE，DE所在直线交于点E，
图1 图2
若，，则____度；
若，，求的度数用含m，n的式子表示．
将图1中的线段BC沿DC所在的直线平移，使得点B在点A的右侧，若，，其他条件不变，得到图2，请你求出的度数用含m，n的式子表示．
【答案】解：；
如图，过点E作EH AB，
平分，，
，
平分，，
，
CD，
CD EH，
，，
．
的度数改变．
过点E作EG AB，
平分，DE平分，，，
，，
CD，
CD EG，
，，
．
【知识点】角的计算、角的平分线、平行线的判定与性质
【解析】
【分析】
本题考查了平行线的性质与判定、角平分线的定义和角的计算有关知识．
先过点E作，利用平行线的性质得到，，再根据角平分线的定义求出、的度数，最后根据即可解答；
先过点E作，利用平行线的性质得到，，再根据角平分线的定义求出、的度数，最后根据即可解答；
先过点E作，根据角平分线的定义求出、的度数，再根据平行线的性质求出、的度数，最后利用即可得解．
【解答】
解：过点E作，
，
，
，，
平分，DE平分，，，
，，
；
故答案案为55；
见答案；
见答案．
直线，点P为平面内一点，连接AP，CP．
如图，点P在直线AB，CD之间，当，时，求的度数；
如图，点P在直线AB，CD之间，与的角平分线相交于K，写出与之间的数量关系，并说明理由；
如图，点P在直线CD下方，当，时，写出与之间的数量关系，并说明理由．
【答案】解：如图1，过P作，
，
，
，，
；
．
理由：如图2，过K作，
，
，
，，
，
过P作，
同理可得，，
与的角平分线相交于点K，
，
；
理由：如图3，过K作，
，
，
，，
，
过P作，
同理可得，，
与的角平分线相交于点K，
，
．
【知识点】平行线的性质
【解析】本题主要考查了平行线的性质以及角平分线的定义的运用，解决问题的关键是作平行线构造内错角，依据两直线平行，内错角相等进行计算．
先过P作，根据平行线的性质即可得到，，再根据进行计算即可；
过K作，根据，可得，，进而得到，同理可得，，再根据角平分线的定义，得出，进而得到与的关系；
过K作，根据，可得，，进而得到，同理可得，，再根据角平分线的定义，得出，进而得到．
已知直线，直线与，分别交于C，D两点，点P是直线上的一动点．
如图，若动点P在线段CD之间运动不与C，D两点重合，问在点P的运动过程中是否始终具有这一相等关系？试说明理由；
如图，当动点P在线段CD之外且在直线的上方运动不与C，D两点重合，则上述结论是否仍成立？若不成立，试写出新的结论，并说明理由；
请画出动点P在线段CD之外且在直线的下方运动不与C，D两点重合时的图形，并仿照图、图标出，，，此时，，之间有何等量关系，请直接写出结论，不必说明理由．
【答案】解：成立，理由如下：
过点P作，
，
，
，
，
，
；
不成立，新的结论为，理由为：
过P作，
，
，
，
，
，
；
如图所示，结论为：．
【知识点】平行线的性质
【解析】此题考查了平行线的性质，熟练掌握平行线的性质是解本题的关键．
成立，理由如下：过点P作，利用两直线平行内错角相等得到，根据，得到，再利用两直线平行内错角相等，根据，等量代换即可得证；
不成立，新的结论为，理由为：过P作，同理得到，根据，等量代换即可得证；
画出相应的图形，如图所示，找出三个角间的关系即可．
如图，在平面直角坐标系中，点A在X轴正半轴上，B在Y轴的负半轴，过点B画轴；C是Y轴上一点，连接AC，作．
如图，请直接写出与的数量关系．
如图，在题的条件下，的角平分线与的角平分线相交于点P，求的度数．
如图，在题、的条件下，的角平分线与的角平分线相交于点Q，请直接写出与数量关系．
如图，点C在Y轴的正半轴上运动时，的角平分线所在的直线与的角平分线相交于点P，的大小是否变化？若不变，直接写出其值；若变化，说明理由．
【答案】解：如图，，
，
，
，
，
又，
，
；
如图2，延长AP交MN于点E，
平分、DP平分，
、，
，
，
，
，
；
平分、AQ平分，
、，
，
，
同理得，
；
的大小不变，为；
设，，
，
，即，，
，
，
平分、DB平分，
，，
则，
．
【知识点】三角形综合、角的平分线、平行线的性质、垂线的相关概念及表示
【解析】本题主要考查角平分线的性质、三角形外角性质、平行线的性质等知识点，熟练掌握角平分线的性质、三角形外角性质是解题的关键．
根据、知，由可得，即；
延长AP交MN于点E，结合中结论，利用角平分线可得，再由平行线的性质和三角形外角性质可得；
由AP平分、AQ平分且可得，同理知，根据四边形内角和可得结论；
设、，由得即，根据角平分线的性质及平行线性质可得，，由利用外角性质可得答案．
三角形ABC中，D是AB上一点，交AC于点E，点F是线段DE延长线上一点，连接FC，．
如图1，求证：；
如图2，连接BE，若，，求的度数；
如图3，在的条件下，点G是线段FC延长线上一点，若：：13，BE平分，求的度数．
【答案】证明： BC，
，
．
．
AB；
解：如图2，过点E作EK AB，
，
AB，
EK，
，
；
平分，
，
：：13，
设，则，
BC，
，，
，
，
解得，
，
，
．
【知识点】平行线的判定与性质
【解析】本题主要考查了平行线的性质及判定方法，关键是熟练掌握平行线的判定方法．
根据平行线的判定与性质即可完成证明；
如图2，过点E作EK AB，可得CF AB EK，再根据平行线的性质即可得结论；
根据：：13，可以设，则，然后根据，，求出x的值，进而可得结果．