初中数学人教版（2024）七年级上册1.2.1 有理数练习

这是一份初中数学人教版（2024）七年级上册1.2.1 有理数练习，文件包含人教版数学七上同步讲练专题11有理数与数轴八大题型原卷版doc、人教版数学七上同步讲练专题11有理数与数轴八大题型解析版doc等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。
TOC \ "1-3" \t "正文,1" \h
TOC \ "1-1" \h \u \l "_Tc27958" 【题型1 正数与负数的概念】 PAGEREF _Tc27958 \h 1
\l "_Tc17467" 【题型2 相反意义量的表示】 PAGEREF _Tc17467 \h 2
\l "_Tc24538" 【题型3 相反意义量的应用】 PAGEREF _Tc24538 \h 4
\l "_Tc20646" 【题型4 有理数的概念辨析】 PAGEREF _Tc20646 \h 6
\l "_Tc573" 【题型5 有理数的分类】 PAGEREF _Tc573 \h 8
\l "_Tc13493" 【题型6 数轴的画法及应用】 PAGEREF _Tc13493 \h 10
\l "_Tc3585" 【题型7 数轴上的点所表示的数】 PAGEREF _Tc3585 \h 12
\l "_Tc7347" 【题型8 数轴中点的规律问题】 PAGEREF _Tc7347 \h 14
【知识点1 正数和负数的概念】
大于0的数叫做正数，在正数前面加负号“-”，叫做负数，一个数前面的“+”“-”号叫做它的符号．0既不是正数也不是负数．0是正负数的分界点，正数是大于0的数，负数是小于0的数．
【题型1 正数与负数的概念】
【例1】（2021秋•盐池县期末）在0，，0.，2π，﹣23%，2021这六个数中，非正数的有（ ）个．
A．2B．3C．4D．0
【分析】根据有理数的分类方法，可得：非正数包括负数和0，据此判断出0，，0.，2π，﹣23%，2021这六个数中，非正数有多少个即可．
【解答】解：在0，，0.，2π，﹣23%，2021这六个数中，非正数有3个：0，，﹣23%．
故选：B．
【变式1-1】（2021秋•西城区校级期中）下列各数﹣5、+3、﹣0.2、、0、、﹣11、2.4中，负数有（ ）个．
A．3B．4C．5D．6
【分析】根据负数的定义，即负数为小于0的有理数，再判定负数的个数．
【解答】解：在﹣5、+3、﹣0.2、、0、、﹣11、2.4中，负数有﹣5、﹣0.2、、﹣11，共4个．
故选：B．
【变式1-2】（2021秋•浑源县期中）﹣a是（ ）
A．负数B．正数
C．0D．正负无法确定
【分析】根据正数、0和负数的定义判断．
【解答】解：当a＞0时，﹣a是负数；
当a＜0时，﹣a是正数，
当a＝0时，﹣a＝0，既不是正数，也不是负数，
∴﹣a正负无法确定．
故选：D．
【变式1-3】（2021秋•襄州区校级月考）下列判断正确的个数是（ ）
①加正号的数是正数，加负号的数是负数；②任意一个正数，前面加上“﹣”，就是一个负数；③0是最小的正数；④大于0的数是正数；⑤字母a既是正数，又是负数．
A．0B．1C．2D．3
【分析】根据各小题中的说法，可以判断各个小题中的说法是否正确，最后得出答案．
【解答】解：加正号的数不一定是正数，如+（﹣5）＝﹣5是负数，加负号的数不一定是负数，如﹣（﹣5）＝5是正数，故①错误；
任意一个正数，前面加上“﹣”，就是一个负数，故②正确；
零既不是正数，也不是负数，故③错误；
大于0的数是正数，故④正确；
如果a是正数，就必定不是负数，故⑤错误，
故选：C．
【知识点2 具有相反意义的量】
一般地，对于具有相反意义的量，我们可以把其中一种意义的量规定为正的，并用正数来表示，把与它意义相反的量规定为负的，并用负数来表示．
【题型2 相反意义量的表示】
【例2】（2021春•保山期末）云南省统计局3月16日发布，2021年前两个月，云南省外贸进出口总额545.80亿元，同比增长86.2%．其中，出口363.57亿元，同比增长275.6%，进口182.27亿元，同比下降7.1%．若出口同比增长率记作+275.6%，则进口同比增长率记作（ ）
A．﹣7.1B．﹣7.1%C．182.27D．+7.1%
【分析】利用相反意义量的定义判断即可．
【解答】解：若增长275.6%记作+275.6%，则下降7.1%记作﹣7.1%．
故选：B．
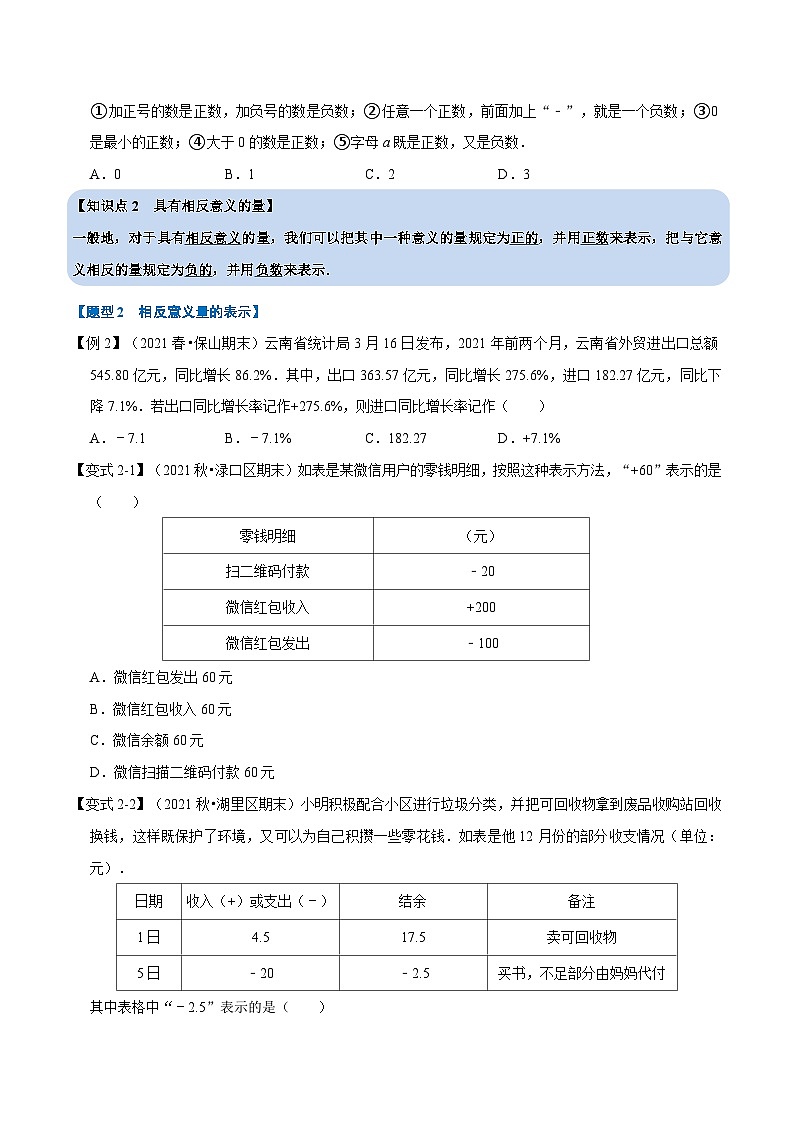
【变式2-1】（2021秋•渌口区期末）如表是某微信用户的零钱明细，按照这种表示方法，“+60”表示的是（ ）
A．微信红包发出60元
B．微信红包收入60元
C．微信余额60元
D．微信扫描二维码付款60元
【分析】此题主要用正负数来表示具有意义相反的两种量：加分记为正，则扣分就记为负，直接得出结论即可．
【解答】解：根据表格中的信息，“+60”表示的是收入60元，
故选：B．
【变式2-2】（2021秋•湖里区期末）小明积极配合小区进行垃圾分类，并把可回收物拿到废品收购站回收换钱，这样既保护了环境，又可以为自己积攒一些零花钱．如表是他12月份的部分收支情况（单位：元）．
其中表格中“﹣2.5”表示的是（ ）
A．卖可回收物换回的钱数
B．买书的钱数
C．买书时妈妈代付的钱数
D．买书的钱与妈妈代付的钱数之和
【分析】根据题目给出的正数和负数的意义解答即可．
【解答】解：表格中“﹣2.5”表示买书时妈妈代付的钱数．
故选：C．
【变式2-3】（2021秋•浑源县期中）某食品厂生产我市特产黄花菜，规定每袋黄花的标准质量为1.5±0.005kg，厂质检部门随机选取了10袋黄花进行质量检测，结果如表所示：
则不符合要求的有（ ）
A．1袋B．2袋C．3袋D．4袋
【分析】根据标准质量为1.5±0.005kg，求出合格的质量的取值范围，再从表格中逐个验证得出答案．
【解答】解：因为每袋黄花的标准质量为1.5±0.005kg，即1.495kg≤m≤1.505kg，
故1.488不符合要求，即不符合要求的有1袋．
故选：A．
【题型3 相反意义量的应用】
【例3】（2021•南京）北京与莫斯科的时差为5小时，例如，北京时间13：00，同一时刻的莫斯科时间是8：00．小丽和小红分别在北京和莫斯科，她们相约在各自当地时间9：00～17：00之间选择一个时刻开始通话，这个时刻可以是北京时间（ ）
A．10：00B．12：00C．15：00D．18：00
【分析】根据北京时间比莫斯科时间早5小时解答即可．
【解答】解：由题意得，北京时间应该比莫斯科时间早5小时，
当莫斯科时间为9：00，则北京时间为14：00；当北京时间为17：00，则莫斯科时间为12：00；
所以这个时刻可以是14：00到17：00之间，
所以这个时刻可以是北京时间15：00．
故选：C．
【变式3-1】（2021秋•玄武区期末）北京与伦敦的时差为8小时，例如，北京时间13：00，同一时刻的伦敦时间是5：00，小丽和小红分别在北京和伦敦，她们相约在各自当地时间9：00～19：00之间选择一个时刻开始通话，这个时刻可以是北京时间（ ）
A．20：00B．18：00C．16：00D．15：00
【分析】根据北京时间比伦敦时间早8小时解答即可．
【解答】解：由题意得，北京时间应该比伦敦时间早8小时，
当伦敦时间为9：00，则北京时间为17：00；当北京时间为19：00，则伦敦时间为11：00；
所以这个时刻可以是北京时间17：00到19：00之间，
所以这个时刻可以是北京时间18：00．
故选：B．
【变式3-2】（2022秋•蒙自市期末）下面的五个时钟显示了同一时刻国外四个城市的时间和北京时间，若下表给出的是国外四个城市与北京的时差，则这四个时钟对应的国外城市从左到右依次是（ ）
A．伦敦、纽约、罗马、悉尼B．罗马、悉尼、伦敦、纽约
C．纽约、悉尼、伦敦、罗马D．罗马、伦敦、悉尼、纽约
【分析】根据纽约、悉尼、伦敦、罗马，与北京的时差，结合钟表确定出对应的城市即可．
【解答】解：由题意可知，北京时间是4时或16时，
由表格可得，悉尼与北京时差为+2，悉尼时间为6时或18时，
纽约与北京时差为﹣13，纽约时间为15时或3时，
伦敦与北京时差为﹣8，伦敦时间为8时或20时，
罗马与北京时差为﹣7，罗马时间为9时或21时，
所以这四个时钟对应的国外城市从左到右依次是纽约、悉尼、伦敦、罗马．
故选：C．
【变式3-3】（2021秋•漳平市期中）下面的4个时钟显示了同一时刻国外三个城市时间和北京时间，根据下表给出的国外三个城市与北京的时差，下列时钟中表示悉尼时间的是（ ）时钟．
A． B．C．D．
【分析】根据伦敦、悉尼、纽约与北京的时差，结合钟表确定出对应的城市即可．
【解答】解：由表格可得，悉尼与北京时差为+2，所以北京时间是4时或16时，悉尼时间为6时或18时．
故选：D．
【知识点3 有理数的概念】
正整数、零和负整数统称整数；正分数和负分数统称分数；整数和分数统称有理数．
【题型4 有理数的概念辨析】
【例4】（2021秋•思明区校级期中）下列说法错误的是（ ）
A．正有理数和负有理数统称有理数
B．负整数和负分数统称为负有理数
C．0是整数，但不是分数
D．正整数、负整数和0统称为整数
【分析】根据有理数相关定义逐一判断即可．
【解答】解：A．正有理数，0和负有理数统称有理数，故选项A符合题意；
B．负整数和负分数统称为负有理数，故选项B不符合题意；
C．0是整数，但不是分数，故选项C不符合题意；
D．正整数、负整数和0统称为整数，故选项D不符合题意．
故选：A．
【变式4-1】（2021秋•榆阳区校级月考）下列关于零的说法中，正确的个数是（ ）
①零是整数，也是有理数；
②零不是正数，也不是负数；
③零不是整数，但是有理数；
④零是整数，但不是自然数；
⑤零既不是整数，也不是分数．
A．0个B．1个C．2个D．3个
【分析】根据有理数的定义逐一判断即可．
【解答】解：①零是整数，也是有理数；正确，符合题意；
②零不是正数，也不是负数；正确，符合题意；
③零是整数，是有理数；原说法错误，不符合题意；
④零是整数，是自然数；原说法错误，不符合题意；
⑤零是整数，不是分数．原说法错误，不符合题意；
故选：C．
【变式4-2】（2021秋•旌阳区校级月考）下面是关于有理数的叙述：①有理数分为正有理数和负有理数两部分；②有理数分为整数和分数两部分；③有理数分为正数、负数和零三部分；④有理数分为正整数、负整数和零三部分；⑤有理数分为正分数、负分数、正整数、负整数和零五部分，其中正确的有（ ）
A．1个B．2个C．3个D．4个
【分析】根据有理数的定义逐一判断即可．
【解答】解：①有理数分为正有理数，0，负有理数三部分，故原说法错误，①不符合题意；
②有理数分为整数和分数两部分，正确，②符合题意；
③有理数分为正有理数、负有理数和零三部分，故原说法错误，③不符合题意；
④整数分为正整数、负整数和零三部分，故原说法错误，④不符合题意；
⑤有理数分为正分数、负分数、正整数、负整数和零五部分，正确，⑤符合题意；
其中正确的有2个，
故选：B．
【变式4-3】（2021秋•鼓楼区校级月考）下列说法中：①0是最小的整数；②有理数不是正数就是负数；③正整数、负整数、正分数、负分数统称为有理数；④非负数就是正数；⑤不仅是有理数，而且是分数；⑥是无限不循环小数，所以不是有理数．其中错误的说法的个数为（ ）
A．6个B．5个C．4个D．3个
【分析】根据有理数的分类标准解决此题．
【解答】解：①根据有理数的大小关系，﹣1＜0，故0不是最小的整数，那么①错误．
②0是有理数，但0既不是正数，也不是负数，那么②错误．
③正整数、负整数、正分数、负分数、0统称为有理数，那么③错误．
④非负数包括0和正数，那么④错误．
⑤根据无理数的定义，是无理数，那么⑤错误．
⑥根据有理数的定义，是有理数，那么⑥错误．
综上：错误的有①②③④⑤⑥，共6个．
故选：A．
【知识点4 有理数的分类】
①按整数和分数的关系分类；②按正有理数、零和负有理数的关系分类．
【题型5 有理数的分类】
【例5】（2021秋•让胡路区校级期末）把下列各数填入相应的集合中：
+6，0.75，﹣3，0，﹣1.2，+8，，，9%，π，﹣0.2020020002…（每相邻两个2之间0的个数逐次加1）．
正分数集合：{ …}；
正整数集合：{ …}；
整数集合：{ …}；
有理数集合：{ …}．
【分析】直接根据有理数的分类进行解答即可．
【解答】解：正分数集合：{0.75，，9%…}；
正整数集合：{+6，+8…}；
整数集合：{+6，﹣3，0，+8…}；
有理数集合：{+6，0.75，﹣3，0，﹣1.2，+8，，，9%…}．
故答案为：0.75，，9%；+6，+8；+6，﹣3，0，+8；+6，0.75，﹣3，0，﹣1.2，+8，，，9%．
【变式5-1】（2021秋•长汀县校级月考）将下列各数填在相应的圆圈里：
+6，﹣8，75，﹣0.4，0，23%，，﹣2006，﹣1.8，．
【分析】根据有理数的分类进行填空即可．
【解答】解：如图：
【变式5-2】（2021秋•牡丹区月考）把下列各数填在相应的大括号里：
，﹣6，0.54，7，0，3.14，20%，π，，3.4365，，﹣2.543．
正整数集合{ …}；
负整数集合{ …}；
分数集合{ …}；
自然数集合{ …}；
负有理数集合{ …}；
正有理数集合{ …}．
【分析】根据有理数的概念和分类可完成此题．
【解答】解：正整数集合{7，…}；
负整数集合{﹣6，}；
分数集合{，0.54，3.14，20%，3.4365，，﹣2.543，…}；
自然数集合{7，0，…}；
负有理数集合{﹣6，，，﹣2.543，…}；
正有理数集合{，0.54，7，3.14，20%，3.4365，…}．
故答案为：7；﹣6，；，0.54，3.14，20%，﹣3.4365，，﹣2.543；7，0；﹣6，，，﹣2.543；，0.54，7，3.14，20%，3.4365．
【变式5-3】（2021秋•恩施市校级月考）把下列各数分别填入相应的大括号内：
自然数集合{ … }；
整数集合{ }；
正分数集合{ … }；
非正数集合{ }；
有理数集合{ }．
【分析】掌握各自的定义：自然数（大于零的整数）；整数（正整数、零和负整数）；有理数（整数和分数的统称）
【解答】解：自然数集合：{0，10…}；
整数集合：{﹣7，0，10，}；
正分数集合：{3.5，，0.03…}；
非正数集合：{﹣7，﹣3.1415，0，﹣3，﹣0.，}；
有理数集合：{﹣7，3.5，﹣3.1415，0，，0.03，﹣3，10，﹣0.，}．
【知识点5 数轴的概念与画法】
数轴的概念：规定了原点、正方向、单位长度的直线叫做数轴．
数轴的画法：①在直线上任取一个点表示数0，这个点叫做原点，②通常规定直线上从原点向右为正方向，从原点向左为负方向；③选取适当的长度为单位长度，直线上从原点向右，每隔一个单位长度取一个点，依次表示1，2，3，……；从原点向左用类似的方法依次表示-1，-2，-3，…….
【题型6 数轴的画法及应用】
【例6】（2021秋•云梦县校级月考）画数轴，并在数轴上表示下列各数．
【分析】利用数轴，把负有理数标在左边相应位置，正有理数标在右边相应位置即可．
【解答】解：如图：
【变式6-1】（2021秋•上蔡县月考）下列六个数中：﹣2.5，3，0，+5，﹣4，．
（1）整数有 个；负分数有 个；既不是正数也不是负数的是 ．
（2）把所有数据分别在数轴上表示出来．
【分析】（1）依据有理数的概念进行解答即可；
（2）把每个数都表示在数轴上即可．
【解答】解：（1）整数有0，+5，﹣4共3个，负分数有﹣2.5，共2个，既不是正数也不是负数的是0．
故答案为：3，2，0；
（2）如图，
【变式6-2】（2021秋•枣阳市期末）邮递员骑车从邮局出发，先向西骑行2km到达A村，继续向西骑行3km到达B村，然后向东骑行9km到达C村，最后回到邮局．
（1）以邮局为原点，向东方向为正方向，用1cm表示1km，画出数轴，并在该数轴上表示A、B、C三个村庄的位置；
（2）C村离A村有多远？
（3）邮递员一共骑行了多少千米？
【分析】（1）根据已知条件在数轴上表示出来即可；
（2）根据题意列出算式，即可得出答案；
（3）根据题意列出算式，即可得出答案．
【解答】解：（1）
；
（2）C村离A村的距离为9﹣3＝6（km）；
（3）邮递员一共行驶了2+3+9+4＝18（千米）．
【变式6-3】（2021秋•渑池县期中）快递员骑车从快递公司出发，先向北骑行200m到达A小区，继续向北骑行400m到达B小区，然后向南骑行1000m到达C小区，最后回到快递公司．
（1）以快递公司为原点，以向南方向为正方向，用1cm表示100m画出数轴，并在该数轴上表示出A、B、C三个小区的位置；
（2）C小区离B小区有多远；
（3）快递员一共骑行了多少千米？
【分析】（1）根据题意画数轴、表示即可；
（2）利用有理数减法可计算出结果；
（3）计算三次行程绝对值的和即可．
【解答】解：（1）由题意把A、B、C三个小区的位置画数轴如图所示：
（2）∵快递员从B小区向南骑行 1000m 到达C小区
∴C小区离B小区的距离是：1000m；
（3）快递员一共骑行的路程为：
OA+AB+BC+OC
＝2BC
＝2×1000
＝2000（米），
2000米＝2千米，
答：快递员一共骑行了2千米．
【知识点6 数轴上的点与有理数之间的关系】
①每个有理数都可以用数轴上的一点来表示，也可以说每个有理数都对应数轴上的一点；
②一般地，设a是一个正数，则数轴上表示数a的点在原点的右边，与原点的距离是a个单位长度；表示-a的点在原点的左边，与原点的距离是a个单位长度.
【题型7 数轴上的点所表示的数】
【例7】（2021秋•正阳县期末）如图，已知纸面上有一数轴，折叠纸面，使﹣3表示的点与1表示的点重合，则与﹣5表示的点对应的点表示的数是（ ）
A．3B．4C．5D．﹣1
【分析】求出折痕和数轴交点表示的数，对折后重合的每一对对应点到此交点距离相等即可求出答案．
【解答】解：∵折叠纸面，使表示﹣3的点与表示1的点重合，
∴折痕和数轴交点表示的数是﹣31，
而表示﹣5的点与此交点距离为﹣1﹣（﹣5）＝4，
∴与表示﹣5的点对应的点表示的数是﹣1+4＝3，
故选：A．
【变式7-1】（2021秋•宣化区期末）如图，在数轴上有A、B、C、D四个点，分别表示不同的四个数，若从这四点中选一点做原点，使得其余三点表示的数中有两个正数和一个负数，则这个点是（ ）
A．点AB．点BC．点CD．点D
【分析】根据数轴上的点原点右边表示正数，原点左边表示负数解决此题．
【解答】解：A．当A为原点，则剩余三个点表示的数均是正数，故A不合题意．
B．当B为原点，则A表示负数，C与D表示正数，故B符合题意．
C．当C为原点，则A与B表示负数，D表示正数，故C不符合题意．
D．当D为原点，A、B与C表示负数，故D不符合题意．
故选：B．
【变式7-2】（2021秋•公安县期末）小聪在纸上画了一条数轴后，折叠纸面，使数轴上表示﹣2的点与表示5的点重合，若数轴上A，B两点之间的距离为10，且A，B两点经上述折叠后重合，则B点表示的数为 ．
【分析】折叠后数轴上表示﹣2的点与表示5的点重合，点﹣2和点5的中点是1.5，数轴上A，B两点经上述折叠后重合，且A，B两点之间的距离为10，则A点与B点到1.5的距离都是5，进而求出B点表示的数即可．
【解答】解：折叠后数轴上表示﹣2的点与表示5的点重合，
折叠点为﹣2和5的中点：1.5．
∵数轴上A，B两点经上述折叠后重合，且A，B两点之间的距离为10，
∴A点与B点到1.5的距离都是5，
当B点在中点右侧时，对应的数为1.5+5＝6.5，
当B点在中点左侧时，对应的数是1.5﹣5＝﹣3.5．
故答案为：6.5或﹣3.5．
【变式7-3】（2022•路北区二模）如图1，点A，B，C是数轴上从左到右排列的三点，分别对应的数为﹣4，b，5．某同学将刻度尺如图2放置，使刻度尺上的数字0对齐数轴上的点A，发现点B对齐刻度尺1.5cm处，点C对齐刻度尺4.5cm处．
（1）在图1的数轴上，AC＝ 个单位长度；
（2）求数轴上点B所对应的数b为 ．
【分析】（1）根据两点之间的距离即可得出答案；
（2）先求出1个单位长度是多少厘米，再求1.5厘米是几个单位长度，根据有理数的加法即可得出答案．
【解答】解：（1）5﹣（﹣4）＝9（个），
故答案为：9；
（2）4.5÷9＝0.5（厘米），
1.5÷0.5＝3（个），
b＝﹣4+3＝﹣1，
故答案为：﹣1．
【题型8 数轴中点的规律问题】
【例8】（2021秋•潍坊期中）如图所示，圆的周长为4个单位长度，A，B，C，D是圆周的4等分点，其中点A与数轴上的原点重合，若将圆沿着数轴向右滚动，那么点A，B，C，D能与数轴上的数字2022所对应的点重合的是 ．
【分析】因为圆沿着数轴向右滚动，依次与数轴上数字顺序重合的是A、D、C、B，且A点只与4的倍数点重合，即数轴上表示4n的点都与A点重合，表示4n+1的数都与D点重合，依此按序类推．
【解答】解：设数轴上的一个整数为x，由题意可知
当x＝4n时（n为整数），A点与x重合；
当x＝4n+1时（n为整数），D点与x重合；
当x＝4n+2时（n为整数），C点与x重合；
当x＝4n+3时（n为整数），B点与x重合；
而2022＝505×4+2，所以数轴上的2022所对应的点与圆周上字母C重合．
故答案为：C．
【变式8-1】（2021秋•广饶县期末）等边△ABC在数轴上的位置如图所示，点A、C对应的数分别是0、﹣1，若△ABC绕顶点沿顺时针方向连续翻转，第一次翻转后点B所对应的数为1，则翻转2022次后点C所对应的数为（ ）
A．不对应任何数B．2020
C．2021D．2022
【分析】此题是图形规律题，表示出前几次翻转，则能发现C点翻转是每三次向正方向移动3个单位的规律，据此可算出第2022次翻转点C移动的距离，则可算出此时点C对应的数．
【解答】解：由图可知，第一次翻转后点C不在数轴上，第二次翻转点C对应数字2，第三次翻转点C不动，
由此可知，每三次翻转点C沿数轴正方向移动3个单位，
∵2022刚好能被3整除，
∴在翻转2022次后，点C沿数轴正方向移动了2022个单位，即点C对应数为﹣1+2022＝2021．
故选：C．
【变式8-2】（2021秋•九龙坡区期末）如图所示，圆的周长为4个单位长度，在圆的4等分点处分别标上数字0，1，2，3，先让圆周上数字0所对应的点与数轴上的数﹣2所对应的点重合，再让圆沿着数轴向右滚动，那么数轴上的数2021将与圆周上的哪个数字重合（ ）
A．0B．1C．2D．3
【分析】分别找出圆周上数字0，1，2，3与数轴上的数重合的数字规律即可解答．
【解答】解：先让圆周上数字0所对应的点与数轴上的数﹣2所对应的点重合，再让圆沿着数轴向右滚动，
则圆周上数字0所对应的点与数轴上的数﹣2，2，6...﹣2+4n，
圆周上数字1所对应的点与数轴上的数﹣1，3，7...﹣1+4n，
圆周上数字2所对应的点与数轴上的数0，4，，
圆周上数字3所对应的点与数轴上的数1，5，+4n，
∵2021＝1+4×505，
∴数轴上的数2021与圆周上数字3重合，
故选：D．
【变式8-3】（2021秋•长汀县期末）如图，把周长为3个单位长度的圆放到数轴（单位长度为1）上，A，B，C三点将圆三等分，将点A与数轴上表示1的点重合，然后将圆沿着数轴正方向滚动，依次为点B与数轴上表示2的点重合，点C与数轴上表示3的点重合，点A与数轴上表示4的点重合，…，若当圆停止运动时点B正好落到数轴上，则点B对应的数轴上的数可能为（ ）
A．2020B．2021C．2022D．2023
【分析】根据圆的滚动规律可知3次一个循环，将各选项中的数字除以3，根据余数可判定求解．
【解答】解：由题意得：圆沿着数轴正方向滚动一次按A，B，C的顺序 排列：
A.2020÷3＝673…1，所以此时点A正好落在数轴上；
B.2021÷3＝673…2，所以此时点B正好落在数轴上；
C.2022÷3＝674，所以此时点C正好落在数轴上；
D.2023÷3＝674…1，所以此时点A正好落在数轴上．
故选：B． 零钱明细
（元）
扫二维码付款
﹣20
微信红包收入
+200
微信红包发出
﹣100
日期
收入（+）或支出（﹣）
结余
备注
1日
4.5
17.5
卖可回收物
5日
﹣20
﹣2.5
买书，不足部分由妈妈代付
序号
1
2
3
4
5
6
7
8
9
10
质量（kg）
1.503
1.502
1.499
1.504
1.496
1.504
1.50
1.503
1.488
1.499
城市
时差/h
纽约
﹣13
悉尼
+2
伦敦
﹣8
罗马
﹣7
城市
伦敦
悉尼
纽约
时差
﹣8
+2
﹣13