2025届浙江省杭州市高三下学期中考数学仿真模拟试题（三模）含答案

这是一份2025届浙江省杭州市高三下学期中考数学仿真模拟试题（三模）含答案，共8页。试卷主要包含了计算下列各式，值最大的是等内容，欢迎下载使用。
选择题：本大题有10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．计算下列各式，值最大的是（ ）
A．1﹣（﹣2）B．1+（﹣2）C．1×（﹣2）D．1÷（﹣2）
2. 下列计算中正确的是（）
A．B．C．D．
3. 下面的图形中，既是轴对称图形又是中心对称图形的是（ ）
AB. C. D.
4. 如图，某一时刻在阳光照射下，广场上的护栏及其影子如图1所示，将护栏拐角处在地面上的部分影子抽象成图2，已知，，则的大小为（）
A. B. C. D.
5．如图，在同一平面直角坐标系中，一次函数y＝k1x+b1与y＝k2x+b2（其中k1k2≠0）的图象分别为直线l1和直线l2，下列结论中一定正确的是（ ）
k1+k2＜0B．k1k2＞0C．b1+b2＜0D．b1b2＞0
6．如图，圆规两脚OA，OB张开的角度∠AOB为α，OA＝OB＝10，则用此圆规所能画出圆的半径为（ ）A．10sinαB．10csαC．D．
7．如图，边长为a的大正方形剪去4个边长为x的小正方形，做成一个无盖纸盒．若无盖纸盒的底面积与外表面积之比为3：5，则根据题意可知a，x满足的关系式为（ ）
A．B．C.D．
8．某校组织450名学生参加测试，随机抽取30人的成绩，得到如下频数分布表，下列说法正确的是（ ）
①该组数据的中位数为90分．
②该组数据的众数在100＜x≤120这一分数段中．
③该组数据的平均数满足：．
④在统计该组数据时，假设漏掉了一个数据，结果平均成绩提高了，则这个数据一定不在100＜x≤120这一分数段中．
A．①②B．③④C．①②③D．②③④
9．关于x的二次函数y＝－x2+2x－m（m≠0）与x轴有两个交点（x1，0），（x2，0）（x1＜x2），关于x的方程x2－2x+m－1＝0有两个非零实数根x3，x4（x3＜x4），则下列关系式不成立的是（ ）
A．x3＜x1＜x2＜x4B．C．D．x1－x3＝x4－x2
10．如图，正方形ABCD的边长是3，BP＝CQ，连接AQ，DP交于点O，并分别与边CD，BC交于点F，E，连接AE，下列结论正确的是（ ）
A．OA2＝OE•OPB．OQ2＝OA•OFC．若BP＝1，则OE＝2D．若BP＝1，则
填空题：本大题有6个小题，每小题3分，共18分.
11.计算|-2024|＝ ．
12. 因式分解：xy2﹣4x＝ ．
已知方程组（）， 则的值为．
14．传统服饰日益受到关注，如图1为明清时期女子主要裙式之一的马面裙，如图2马面裙可以近似地看作扇环，其中AD长度为米，BC长度为米，圆心角∠AOD＝60°，则裙长AB为 ．
15．如图，在中，,点在边上，且平分的周长，则tan∠ADB= ．
第15题
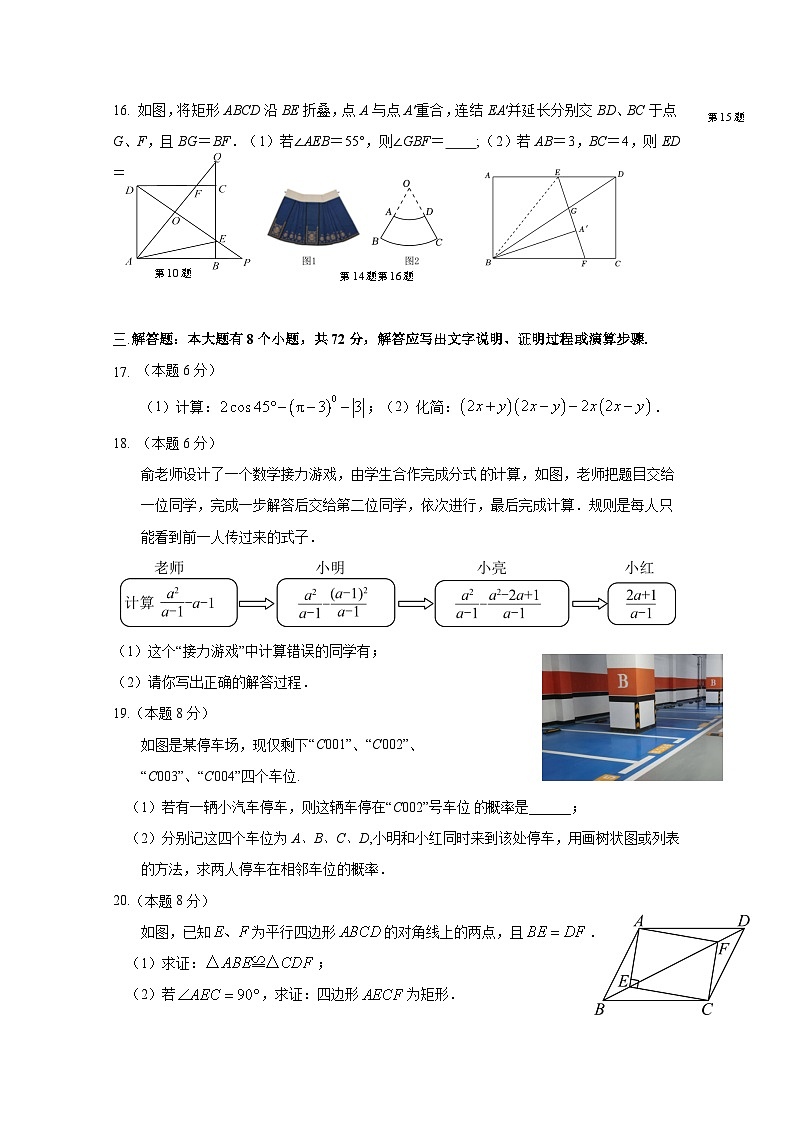
16. 如图，将矩形ABCD沿BE折叠，点A与点A′重合，连结EA′并延长分别交BD、第14题第16题
第10题
BC于点G、F，且BG＝BF．（1）若∠AEB＝55°，则∠GBF＝ ;（2）若AB＝3，BC＝4，则ED＝ ．
三.解答题：本大题有8个小题，共72分，解答应写出文字说明、证明过程或演算步骤.
（本题6分）
（1）计算：；（2）化简：．
18. （本题6分）
俞老师设计了一个数学接力游戏，由学生合作完成分式计算，如图，老师把题目交给一位同学，完成一步解答后交给第二位同学，依次进行，最后完成计算．规则是每人只能看到前一人传过来的式子．
（1）这个“接力游戏”中计算错误的同学有；
（2）请你写出正确的解答过程．
19.（本题8分）
如图是某停车场，现仅剩下“C001”、“C002”、
“C003”、“C004”四个车位.
（1）若有一辆小汽车停车，则这辆车停在“C002”号车位概率是______；
（2）分别记这四个车位为A、B、C、D,小明和小红同时来到该处停车，用画树状图或列表的方法，求两人停车在相邻车位的概率．
20.（本题8分）
如图，已知为平行四边形的对角线上的两点，且．
（1）求证：；
（2）若，求证：四边形为矩形．
21．（本题10分）
已知一次函数y1＝kx+b（k，b为常数，k≠0）的图象与反比例函数（m是常数，m≠0）的图象交于A（1，t+1），B（t﹣5，﹣1）两点．
求一次函数和反比例函数的解析式；
若，请直接写出的取值范围；
（3）若（c，p），（n，q）是反比例函数图象上的两点，且满足c＝n+1，求的值．
22.（本题10分）
如图是400米跑道示意图，中间的足球场ABCD是矩形，两边是半圆，直道AB的长是多少？你一定知道是100米!可你也许不知道，这不仅仅为了比赛的需要，还有另外一个原因，等你做完本题就明白了．设AB＝x米．
（1）请用含x的代数式表示BC．
（2）设矩形ABCD的面积为S．
①求出S关于x的函数表达式．
②当直道AB为多少米时，矩形ABCD的面积最大？并求出此时矩形ABCD的最大面积.
23.（本题12分）综合与实践
【基础巩固】（1）如图1，在△ABC中，D是BC的中点，E是AC的一个三等分点，且．连结AD，BE交于点G，则AG：GD＝ ；BG：GE＝ ．
【尝试应用】（2）如图2，在△ABC中，E为AC上一点，AB＝AE，∠BAD＝∠C，若AD⊥BE，CE＝1，AE＝3，求AD的长．
【拓展提高】（3）如图3，在平行四边形ABCD中，F为BC上一点，E为CD中点，BE与AC，AF分别交于点G，M，若∠BAF＝∠DAC，AB＝AG，BF＝2，BM＝2MG，求AM的长．
（本题12分）
已知：如图1，是的内接三角形，且，点是弧上一动点，连接交弦于点，点在弦上，且．
（1）求证：；
（2）如图2，若是的直径，，，求直径的长；
（3）如图3，保持点位置不变，调整点的位置使得直线经过圆心，点在上，使得成立的所有点中，有一个点的位置始终不变，试在图中找出这个点，并说明理由．
数学答案
一.选择题：本大题有10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.
填空题：本大题有6个小题，每小题3分，共18分.
(y+2)(y-2)____________；13._______2______；
14.____________；15._____________；16.___40°__________.
三.解答题：本大题有8个小题，共72分，解答应写出文字说明、证明过程或演算步骤.
17.（本题满分6分）
解：
18. （本题满分6分）
（1） 小明、小红 ；（2分，少写或漏写不给分）
（2）请你写出正确的解答过程．（4分）
19.（本题满分8分）
（1）；（2分） （2）树状图或列表，（4分），（2分）
20.（本题满分8分）
（1）证
（2）证明，
四边形为平行四边形（或利用对角线互相平分证）
又，平行四边形矩形．
21.（本题满分10分）
（1）（2）；
（3）
22.（本题满分10分）解：（1）由题意可得：π•BC＝，(2分）∴BC＝；（2分）
（2）①∵四边形ABCD是矩形，
∴S＝×x＝﹣（x﹣100）2+；（几种表达式均可，2分）
②当x＝100时（2分），S最大=（2分）
23.（本题满分12分）
（1）1：1；3：1；
（2）AD的长为；
（3）AM的长为．
（本题满分12分）
（1）解：∵在中，，∴，
∵在中，，∴，又∵∴，∴，∵，∴；
（2）∵，∴，∵，∴
又∵是的直径，∴，，∴,
∴，∴∴，设，则，，∴，∵，即∴，∴，∴，
（3）解：延长，交圆于点M.
∵，∴，，
∴，∴∵，∴，∴，∴，∴始终不变的点是半径（或）的延长线与圆的交点．
题号
1
2
3
4
5
6
7
8
9
10
答案
A
A
B
B
B
C
A
B
B
D