浙教版数学八年级上册期末复习重难点01 全等三角形（5种模型）（2份，原卷版+解析版）

这是一份浙教版数学八年级上册期末复习重难点01 全等三角形（5种模型）（2份，原卷版+解析版），文件包含浙教版数学八年级上册期末复习重难点01全等三角形5种模型原卷版doc、浙教版数学八年级上册期末复习重难点01全等三角形5种模型解析版doc等2份试卷配套教学资源，其中试卷共90页， 欢迎下载使用。
一、倍长中线
倍长中线是指加倍延长中线，使所延长部分与中线相等，然后往往需要连接相应的顶点，则对应角对应边都对应相等。常用于构造全等三角形。中线倍长法多用于构造全等三角形和证明边之间的关系（通常用“SAS”证明）（注：一般都是原题已经有中线时用，不太会有自己画中线的时候）。
题干中出现三角形一边的中线（与中点有关的线段），或中点，通常考虑倍长中线或类中线，构造全等三角形.把该中线延长一倍，证明三角形全等，从而运用全等三角形的有关知识来解决问题的方法.
主要思路：倍长中线（线段）造全等
在△ABC中 AD是BC边中线

延长AD到E， 使DE=AD，连接BE

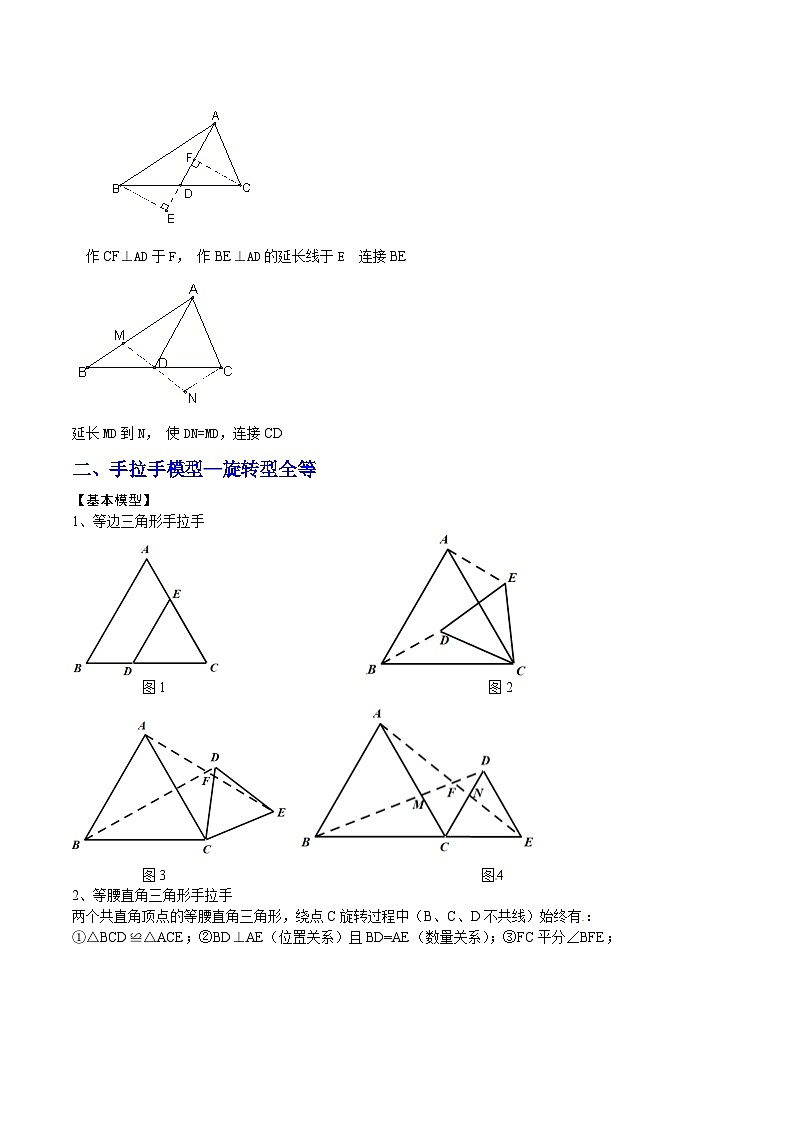
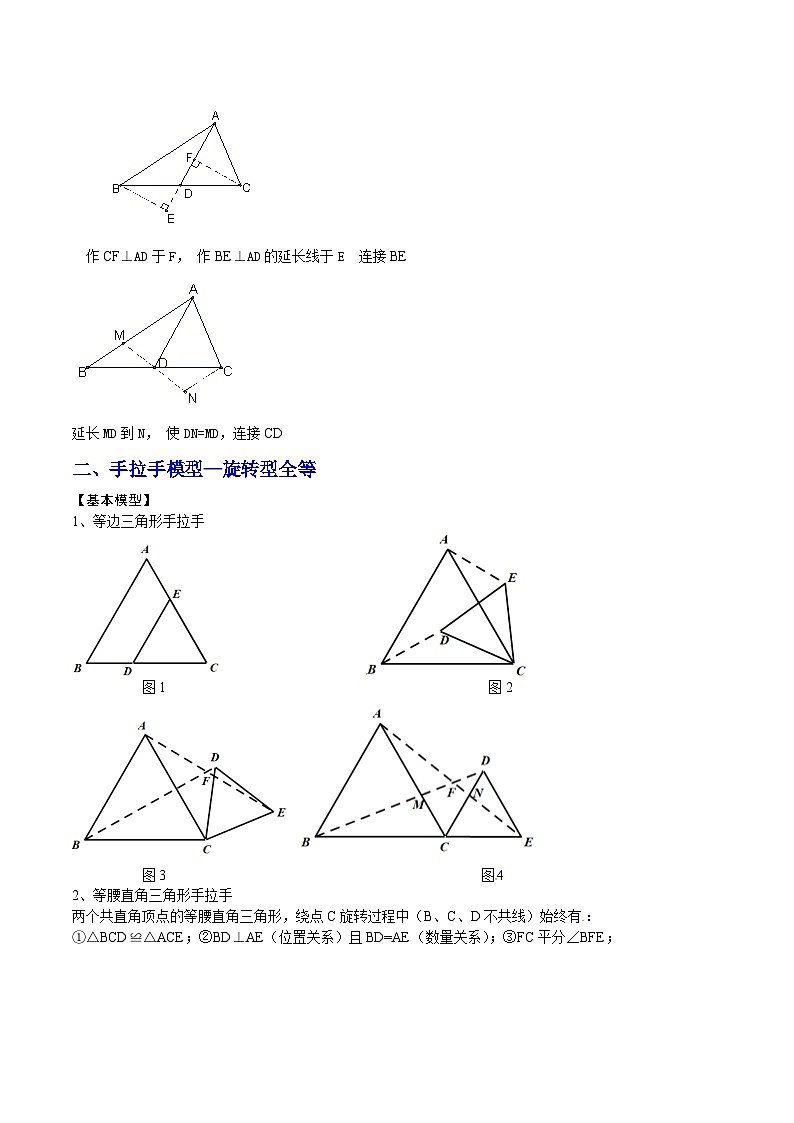
作CF⊥AD于F， 作BE⊥AD的延长线于E 连接BE

延长MD到N， 使DN=MD，连接CD
二、手拉手模型—旋转型全等
【基本模型】
1、等边三角形手拉手

图1 图2
[来源:
图3 图4
2、等腰直角三角形手拉手
两个共直角顶点的等腰直角三角形，绕点C旋转过程中（B、C、D不共线）始终有：[来源:Z#xx#k.Cm]
①△BCD≌△ACE；②BD⊥AE（位置关系）且BD=AE（数量关系）；③FC平分∠BFE；

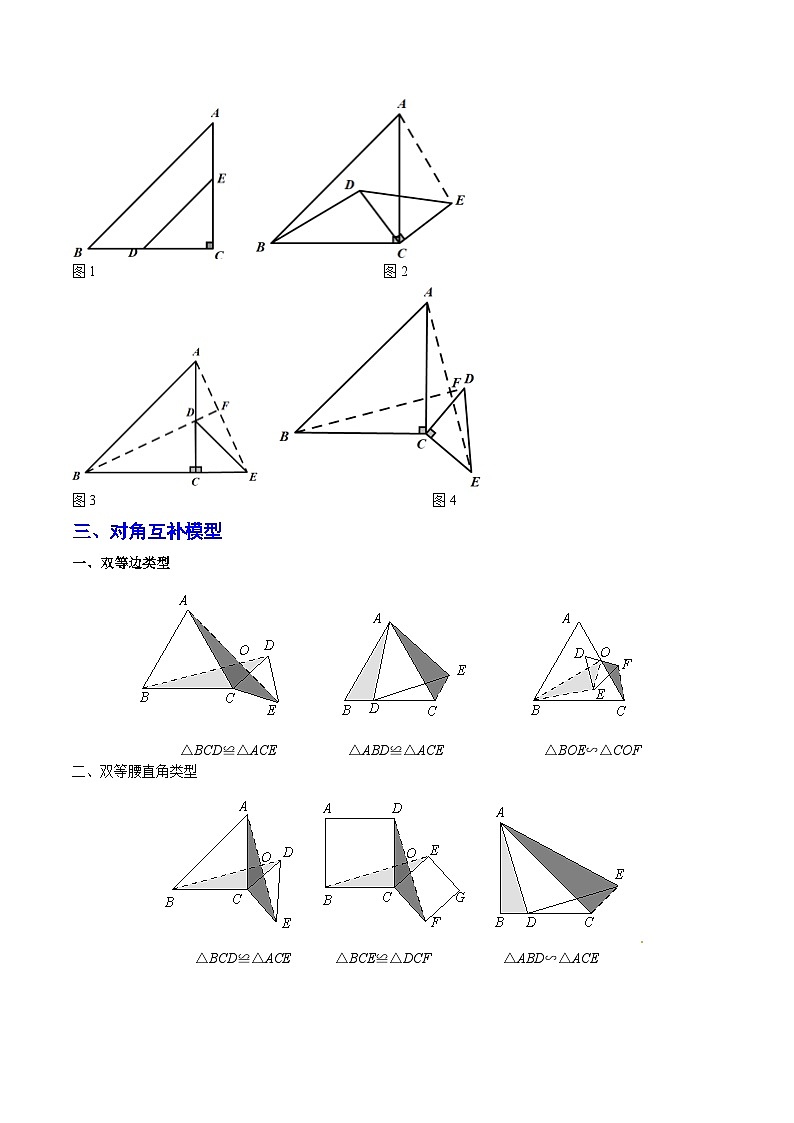
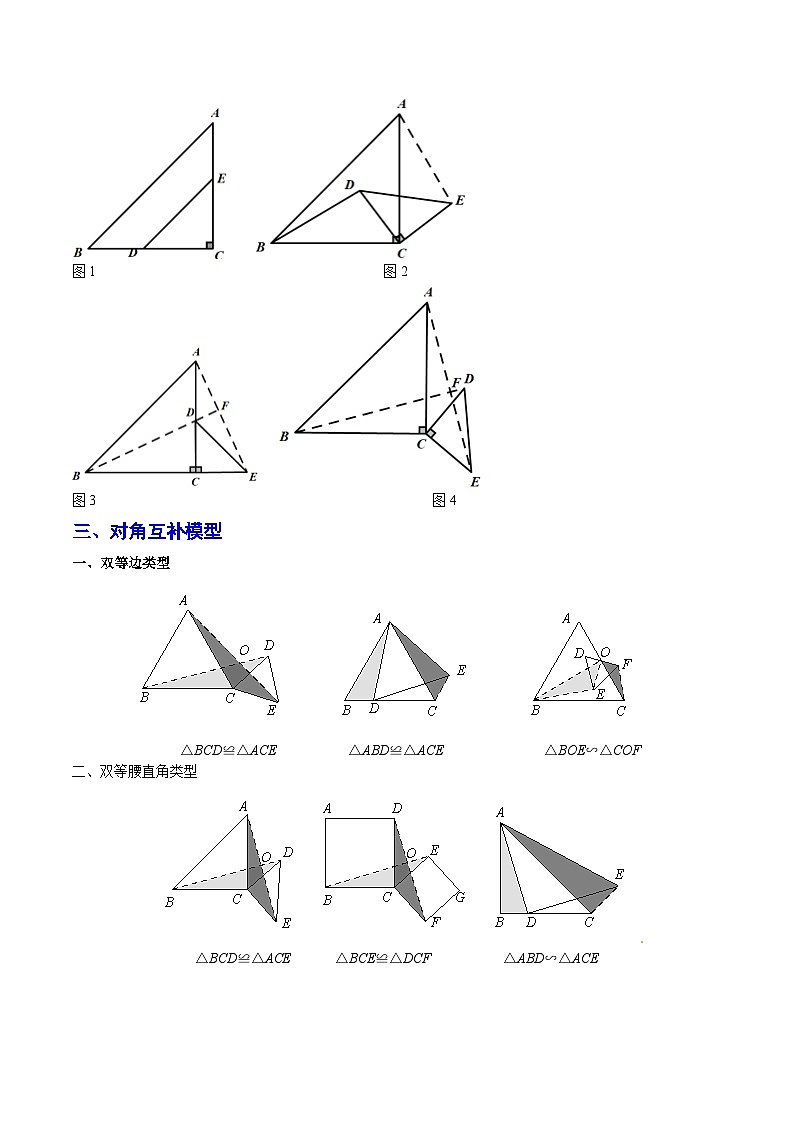
图1 图2

图3 图4
三、对角互补模型
一、双等边类型

△BCD≌△ACE△ABD≌△ACE△BOE∽△COF
二、双等腰直角类型
△BCD≌△ACE△BCE≌△DCF△ABD∽△ACE
四、角平分线+垂直构造全等三角形
【模型】一、角平分线垂两边
角平分线+外垂直
当已知条件中出现为的角平分线、于点时，辅助线的作法大都为过点作即可.即有、≌等，利用相关结论解决问题.
【模型】二、角平分线垂中间
角平分线+内垂直
当已知条件中出现为的角平分线,于点时，辅助线的作法大都为延长交于点即可.即有是等腰三角形、是三线等，利用相关结论解决问题.
【模型】三、角平分线构造轴对称
角平分线+截线段等
当已知条件中出现为的角平分线、不具备特殊位置时，辅助线的作法大都为在上截取，连结即可.即有≌，利用相关结论解决问题.
【模型】四、角平分线加平行线等腰现
角平分线+平行线[来
当已知条件中出现为的角平分线，点角平分线上任一点时，辅助线的作法大都为过点作//或//即可.即有是等腰三角形，利用相关结论解决问题.
五、一线三等角模型
过等腰直角三角形的另外两个顶点作该直线的垂线段，会有两个三角形全等（AAS）
常见的两种图形：

图1 图2
能力拓展
题型一：倍长中线
一、单选题
1．（2020·浙江·高照实验学校八年级阶段练习）如图，在△ABC中，AB＝8，AC＝6，AD是BC边上的中线，则AD长的取值范围是( )
A．6