2024-2025学年江苏省苏州市草桥中学校八年级（上）11月期中考试数学试卷（含答案）

这是一份2024-2025学年江苏省苏州市草桥中学校八年级（上）11月期中考试数学试卷（含答案），共13页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。
一、选择题：本题共8小题，每小题3分，共24分。在每小题给出的选项中，只有一项是符合题目要求的。
1.下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是( )
A. B. C. D.
2.下列四个数中，无理数的是( )
A. 4B. 227C. 0D. π
3.2024年国庆假期期间，苏州文旅市场持续七天“人从众”模式，不断升温的消费热情，让网友直呼：“这来了得有一亿人”.据当地通信运营商数据，今年国庆假期，苏州全市累计接待游客1.28×107人次．其中1.28×107精确到( )
A. 十万位B. 百万位C. 十分位D. 百分位
4.下列二次根式中是最简二次根式的是( )．
A. 0.5B. 3C. 8D. 4
5.等腰三角形的两边a、b满足 a−2+b−52=0，那么这个三角形的周长是( )
A. 9或12B. 9C. 12D. 10
6.如图，在Rt▵ABC中，∠B=90∘，以点A为圆心，适当长为半径画弧，分别交AB、AC于点D，E，再分别以点D、E为圆心，大于12DE为半径画弧，两弧交于点F，作射线AF交边BC于点G，若BG=1，AC=4，则▵ACG的面积是( )
A. 2B. 3C. 4D. 5
7.如图，圆柱形玻璃容器高8cm，底面圆的周长为16cm，在外侧距下底1cm的点A处有一蜘蛛，与蜘蛛相对的圆柱形容器的上口外侧距上口1cm的点B处有一只苍蝇，则蜘蛛捕获苍蝇所走的最短路线长度是( )
A. 16cmB. 2 73cm
C. 14cmD. 10cm
8.如图，Rt▵ABC中，分别以这个三角形的三边为边长作正方形，面积分别记为S1、S2、S3，若S1+S3−S2=20，则阴影部分面积为( )
A. 10B. 5C. 20D. 15
二、填空题：本题共8小题，每小题3分，共24分。
9.16的算术平方根是 ．
10.要使二次根式 x−2有意义，则x应满足条件 ．
11.等腰三角形的顶角的度数为80∘，则它的底角的度数为 ．
12.比较大小： 2 3．
13. 13的整数部分记为a，算术平方根等于本身的正整数记为b，那么7a+6b的立方根是 ．
14.如图，▵ABC的边BC,AC的垂直平分线l1,l2相交于点O.若∠A=110∘，则∠BOC= °.
15.如图，在Rt▵ABC中，∠ACB=90∘，AB= 5，BC=1，点D为斜边AB的中点，连接CD，将▵BCD沿CD翻折，使B落在点E处，点F为直角边AC上一点，连接DF，将▵ADF沿DF翻折，使点A与点E重合，则AF的长为 ．
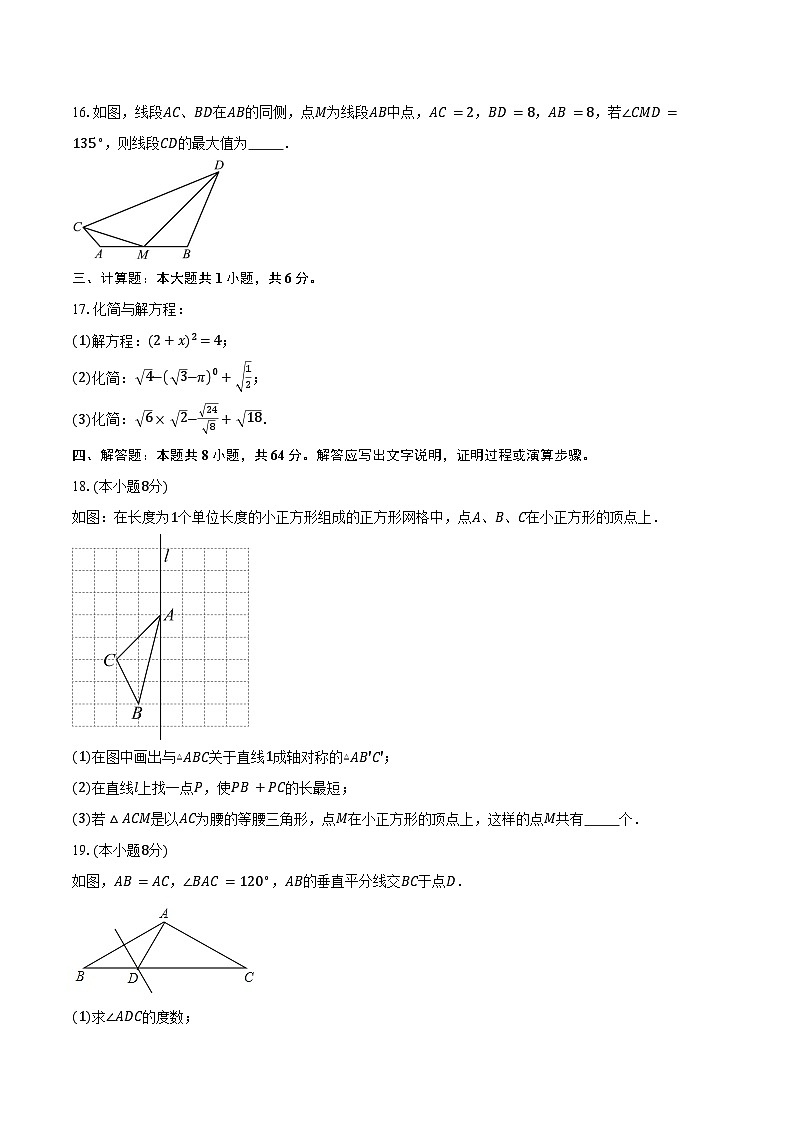
16.如图，线段AC、BD在AB的同侧，点M为线段AB中点，AC=2，BD=8，AB=8，若∠CMD=135∘，则线段CD的最大值为 ．
三、计算题：本大题共1小题，共6分。
17.化简与解方程：
(1)解方程：2+x2=4；
(2)化简： 4− 3−π0+ 12；
(3)化简： 6× 2− 24 8+ 18．
四、解答题：本题共8小题，共64分。解答应写出文字说明，证明过程或演算步骤。
18.(本小题8分)
如图：在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．
(1)在图中画出与▵ABC关于直线1成轴对称的▵AB′C′；
(2)在直线l上找一点P，使PB+PC的长最短；
(3)若△ACM是以AC为腰的等腰三角形，点M在小正方形的顶点上，这样的点M共有 个．
19.(本小题8分)
如图，AB=AC，∠BAC=120∘，AB的垂直平分线交BC于点D．
(1)求∠ADC的度数；
(2)求证：DC=2DB．
20.(本小题8分)
实数a，b在数轴上对应点的位置如图所示，M= a−22− b+22− a2．
(1)化简M；
(2)当a= 3−1，b=− 3−1时，求M的值．
21.(本小题8分)
有一块长方形木板，木工师傅采用如图所示的方式，在木板上截出两块面积分别为45dm2和80dm2的两块正方形木板．
(1)截出的两块正方形木板的边长分别为 dm， dm；
(2)剩余木板的面积为 dm2；
(3)如果木工师傅想从剩余的木板中截出长为2dm，宽为1.5dm的长方形木条，最多能截出 个这样的木条．
22.(本小题8分)
2024年4月14日7∶30，2024苏州马拉松在苏州市金鸡湖畔鸣枪起跑，比赛赛道先后经过金鸡湖、盘门、寒山寺、干将路、文化艺术中心等城市地标及人文景观．学生小明操控无人机记录下了赵老师在干将路PQ段参赛过程．小明在点B处发现在点A处的赵老师以每分钟250米的速度从P向Q匀速前进，1分钟后他发现赵老师已经跑到了离他200米的位置点C处．
(1)若∠ABC=90∘，请求出AB的长度；
(2)在(1)的条件下，点M以250m/min的速度从点A出发，在点M前方90米的点N以200m/min的速度匀速前进，在点M追上点N前，经过多少分钟，▵BMN是以MN为底的等腰三角形．
23.(本小题8分)
如图，E为AC上一点，AC⊥BC，AC⊥AD，AB=DE，AB，DE交于点F，且AB⊥DE．
(1)试说明BC+CE=AD；
(2)连接BD，BE，若设BC=a，AC=b，AB=c，利用此图证明勾股定理．
24.(本小题8分)
张同学在深入研究课本82页第2题时发现：
(1)如图(1)，一架梯子AB斜靠在竖直墙OA上，梯子底端点B距离墙角O的距离是3m，此时梯子到达的垂直高度OA是4m，通过计算可以得到梯子AB的长为 m，爱动脑筋的张同学发现，梯子AB的中点为M，当梯子底端从B向右滑动到点D的过程中，中点M到O的距离 .(填变大、不变、变小)张同学继续研究发现，在梯子AB沿着墙OA滑动过程中，∠OAB的角平分线AE交OB于点H．
(2)如图(2)，过点B作BE⊥AH，交AH的延长线于点E，连接OE，在AB滑动的过程中，线段OE，BE有何数量关系，并说明理由；
(3)在AB滑动的过程中，▵AOB面积的最大值为 ．
25.(本小题8分)
操作体验：数学活动《折纸与证明》中，有这样一段活动材料：

①如图1−①，把正方形ABCD对折后再展开，折痕为EF；
②如图1−②，将点A翻折到EF上的点A′处，且使折痕过点B；
③如图1−③，沿A′C折叠，得▵A′BC(如图1−④)．
(1)根据以上操作，结合图2试证明▵A′BC是等边三角形；
(2)初步探究：将AB沿BE翻折到BP位置，延长EP交CD于点Q，如图3，求证：点Q是CD的三等分点．
(3)深入探究：如图4，点M在AB上移动，将BC沿CM翻折到点B′，连接CM、DB′并延长交于点H，N是DB′的中点，连接CN，AH，请直接写出HA、HC、HD之间的等量关系 ．
参考答案
1.B
2.D
3.A
4.B
5.C
6.A
7.D
8.B
9.4
10.x≥2/2≤x
11.50∘/50度
12.<
13.3
14.140
15.34/0.75
16.10+4 2
17.【小题1】
解：2+x2=4
∴2+x=±2，
∴x=0或x=−4；
【小题2】
解：原式=2−1+ 22
=1+ 22；
【小题3】
解∶原式= 12− 248+ 18
=2 3− 3+3 2
= 3+3 2．

18.【小题1】
解：如图所示，▵AB′C′′即为所求；
【小题2】
如图所示，点P即为所求；
【小题3】
4

19.【小题1】
∵AB=AC，∠BAC=120∘，
∴∠B=12(180∘−∠BAC)=12(180∘−120∘)=30∘，
∵AB的垂直平分线交BC于点D．
∴AD=BD，
∴∠BAD=∠B=30∘，
∴∠ADC=∠B+∠BAD=30∘+30∘=60∘；
【小题2】
∵∠ADC=60∘，∠C=30∘，
∴∠DAC=90∘，
∴AD=12CD，∠BAD=30∘，
∴∠B=∠BAD，
∴BD=AD，
∴DC=2DB．

20.【小题1】
解：由数轴可得：b