

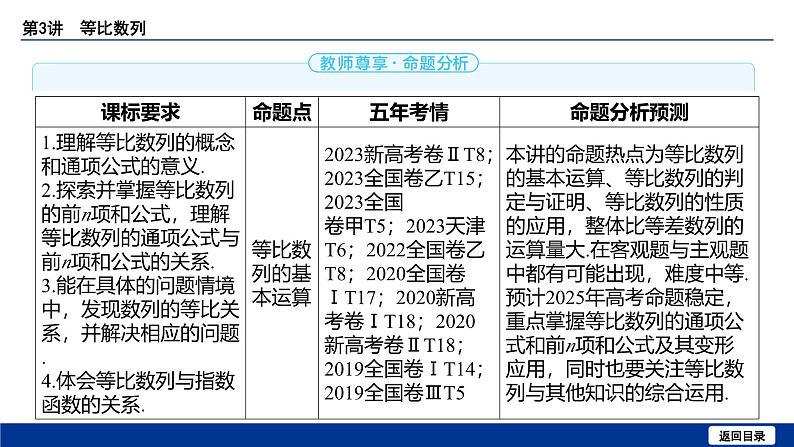
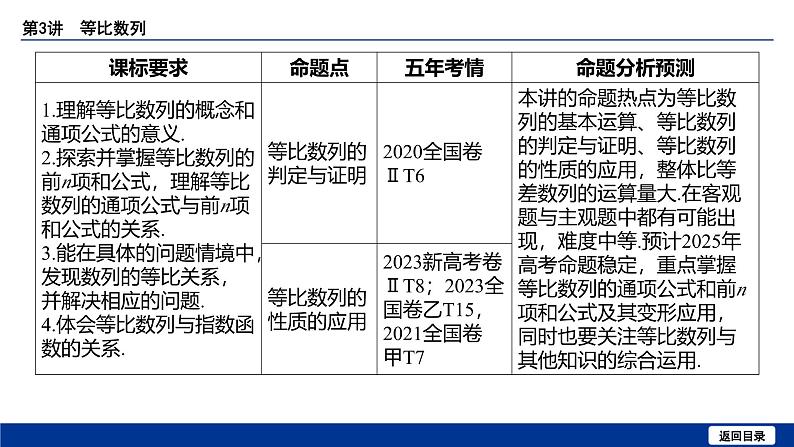




备战2025年高考数学精品课件第五章 第3讲 等比数列
展开
这是一份备战2025年高考数学精品课件第五章 第3讲 等比数列,共60页。PPT课件主要包含了2等比中项的概念,规律总结,等比数列的单调性,等比数列的性质,或-10,方法技巧,ACD,-∞3等内容,欢迎下载使用。
1. 等比数列的概念(1)等比数列的定义一般地,如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,
那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母 q ( q
≠0)表示.注意 (1)等比数列中的任何一项都不为0,且公比 q ≠0.(2)若一个数列是常数列,
则此数列一定是等差数列,但不一定是等比数列,如:0,0,0,….
如果在 a 与 b 中间插入一个数 G ,使 a , G , b 成等比数列,那么 G 叫做 a 与 b 的等
比中项,此时 G 2= ab .
注意 只有当两个数同号且不为0时,才有等比中项,且等比中项有两个.
(3)等比数列的通项公式及其变形
通项公式:① ,其中 a 1是首项, q 是公比.
通项公式的变形: an = am · qn - m .
an = a 1· qn -1
当 q =1时,{ an }是常数列;当 q <0时,{ an }是摆动数列.
2. 等比数列的前 n 项和
设等比数列{ an }的公比为 q ,前 n 项和为 Sn .
当 q =1时,因为 a 1≠0,所以 Sn = na 1.由此可知,数列{ Sn }的图象是函数 y = a 1 x
的图象上一系列孤立的点.
注意 在运用等比数列的前 n 项和公式时,要注意对 q =1与 q ≠1进行讨论.
- aqn
(1)等比数列项的性质
设数列{ an },{ bn }是等比数列.
a.若 m + n = k + l ,则⑤ ,其中 m , n , k , l ∈N*,反之,不一定
成立,如当数列{ an }是非零常数列时,此结论不成立.
b.相隔等距离的项组成的数列仍是等比数列,即 ak , ak + m , ak +2 m ,…( k , m ∈N*)
仍是等比数列,公比为⑥ .
d.若 an >0,则数列{lg an }是等差数列.
aman = akal
(2)等比数列的前 n 项和的性质
设 Sn 是等比数列{ an }的前 n 项和.
a. Sm + n = Sn + qnSm = Sm + qmSn .
b.当 q ≠-1(或 q =-1且 k 为奇数)时, Sk , S 2 k - Sk , S 3 k - S 2 k ,…是⑦
数列.
注意 当 q =-1且 k 为偶数时, Sk , S 2 k - Sk , S 3 k - S 2 k ,…不是等比数列.
1. 下列说法正确的是( B )
2. [多选]已知数列{ an }是等比数列,公比为 q ,前 n 项和为 Sn ,则下列说法错误的
是( BC )
3. [易错题]设等比数列{ an }的前 n 项和为 Sn ,若 a 1=2, S 3=6,则 S 4= .
4. [教材改编]有四个数,前三个数成等比数列,后三个数成等差数列,第一个数与
第四个数的和为21,中间两个数的和为18,则这四个数依次为
.
3,6,12,18或
命题点1 等比数列的基本运算
例1 (1) [2023全国卷甲]设等比数列{ an }的各项均为正数,前 n 项和为 Sn ,若 a 1=
1, S 5=5 S 3-4,则 S 4=( C )
解法二 设等比数列{ an }的公比为 q ,由已知得1+ q + q 2+ q 3+ q 4=5(1+ q + q 2)
-4,整理得 q (1+ q )( q 2-4)=0,由于此数列各项均为正数,所以 q =2,所以 S 4
=1+ q + q 2+ q 3=1+2+4+8=15.故选C.
(2)[2023天津高考]已知{ an }为等比数列, Sn 为数列{ an }的前 n 项和, an +1=2 Sn +
2,则 a 4的值为( C )
1. 等比数列基本运算中常用的数学思想
训练1 (1)[2022全国卷乙]已知等比数列{ an }的前3项和为168, a 2- a 5=42,则 a 6=
( D )
(2)[全国卷Ⅰ]设{ an }是等比数列,且 a 1+ a 2+ a 3=1, a 2+ a 3+ a 4=2,则 a 6+ a 7+
a 8=( D )
命题点2 等比数列的判定与证明
(1)求 b 1, b 2, b 3;
(2)判断数列{ bn }是否为等比数列,并说明理由;
(3)求{ an }的通项公式.
判定与证明等比数列的常用方法
训练2 [2023江苏省七市模拟]已知数列{ an }满足 a 1=1, a 2=5, an +2=5 an +1-6
an .
(1)证明:{ an +1-2 an }是等比数列.
[解析] 解法一 (1)∵ an +2=5 an +1-6 an ,∴ an +2-2 an +1=5 an +1-6 an -2 an +1=3 an +1-6 an =3( an +1-2 an ),∵ a 1=1, a 2=5,∴ a 2-2 a 1=3≠0,∴数列{ an +1-2 an }是首项为3,公比为3的等比数列.
(2)证明:存在两个等比数列{ bn },{ cn },使得 an = bn + cn 成立.
[解析] 解法一 (2)∵ an +2=5 an +1-6 an ,∴ an +2-3 an +1=5 an +1-6 an -3 an +1
=2 an +1-6 an =2( an +1-3 an ).∵ a 1=1, a 2=5,∴ a 2-3 a 1=2≠0,∴数列{ an +1-3 an }是首项为2,公比为2的等比数列,∴ an +1-3 an =2 n ①,由第(1)问得 an +1-2 an =3 n ②,由②-①得, an =3 n -2 n .故存在通项为 bn =3 n , cn =-2 n 的两个等比数列,使得 an = bn + cn 成立.
解法二 (2)由(1)知 an +1-2 an =3 n ①,
由 an +2-3 an +1=2( an +1-3 an )可得 an +1-3 an =2 n ②,
由①-②得, an =3 n -2 n ,故存在通项为 bn =3 n , cn =-2 n 的两个等比数列,使得 an = bn + cn 成立.
命题点3 等比数列的性质的应用
例3 (1)[2023新高考卷Ⅱ]记 Sn 为等比数列{ an }的前 n 项和,若 S 4=-5, S 6=21 S 2,
则 S 8=( C )
(2)[2023全国卷乙]已知{ an }为等比数列, a 2 a 4 a 5= a 3 a 6, a 9 a 10=-8,则 a 7
= .
解法二 设数列{ an }的公比为 q .因为 a 4 a 5= a 3 a 6≠0,所以 a 2=1.又 a 9 a 10= a 2 q 7· a 2 q 8= q 15=-8,于是 q 5=-2,所以 a 7= a 2 q 5=-2.
训练3 (1)[2021全国卷甲]记 Sn 为等比数列{ an }的前 n 项和.若 S 2=4, S 4=6,则 S 6=
( A )
[解析] 解法一 由题意知 a 1 a 5= a 2 a 4=144 ①, a 2+ a 4=
(2)若公比大于1的等比数列{ an }满足 a 1 a 5=144, a 2+ a 4=30,则公比 q = .
1. [命题点1/2023武汉调研]设正项等比数列{ an }的前 n 项和为 Sn ,若2 S 3=3 a 2+8 a 1, S 8=2 S 7+2,则 a 2=( A )
2. [命题点1/新高考卷Ⅱ]已知公比大于1的等比数列{ an }满足 a 2+ a 4=20, a 3=8.
(1)求{ an }的通项公式;
(2)求 a 1 a 2- a 2 a 3+…+(-1) n -1 anan +1.
4. [命题点3/多选/2023鄂东南省级示范高中联考]设等比数列{ an }的公比为 q ,其前 n
项和为 Sn ,前 n 项积为 Tn ,且满足条件 a 1>1, a 2 022 a 2 023>1,( a 2 022-1)( a 2 023-
1)<0,则下列选项正确的是( ACD )
1. [2024南昌市模拟]已知公比为 q 的等比数列{ an }的前 n 项和 Sn =2 a 1-2 qn ,则 a 1
=( B )
2. [2023湖北黄冈模拟]已知数列{ an }是正项等比数列,数列{ bn }满足 bn =lg2 an .若
a 2 a 5 a 8=212,则 b 1+ b 2+ b 3+…+ b 9=( C )
3. [2024山东济南联考]记 Sn 为等比数列{ an }的前 n 项和,若 S 4=5 S 2, S 6=21,则 S 8=( C )
4. [2023济南市模拟]在数列{ an }中,若 an =2 n +2 n -1×3+2 n -2×32+2 n -3×33+…
+22×3 n -2+2×3 n -1+3 n ,则 a 2 023=( C )
5. 公元前1650年左右的埃及《莱因德纸草书》上载有如下问题:“十人分十斗玉
米,从第二人开始,各人所得依次比前人少八分之一,问每人各得玉米多少斗.”在
上述问题中,第一人分得玉米( C )
6. [2024广东七校联考]在等比数列{ an }中,公比为 q .已知 a 1=1,则0< q <1是数列
{ an }是递减数列的( C )
7. [2024河南省模拟]已知等比数列{ an }的前 n 项和为 Sn ,且公比 q ≠-1,若 S 12= S 4+16 S 8,则公比 q =( B )
10. [2024福州市一检]已知等比数列{ an }的前 n 项和为 Sn ,且 an +1= Sn +2.
解法二 (1)因为 an +1= Sn +2 ①,
所以当 n ≥2时, an = Sn -1+2 ②,
由①式得 a 2= a 1+2,得 a 1=2,所以 an =2 n .
(2)若 bn =lg2 a 2 n -1,求数列{ bn }的前 n 项和 Tn .
12. [2024辽宁大连二十四中模拟]设 Sn 为数列{ an }的前 n 项和,已知 a 1=3,∀ m , n
∈N*, Sm + n = SmSn ,则( B )
15. [2024贵阳市模拟]设 Sn 为数列{ an }的前 n 项和.已知4 an -3 Sn = n .
(1)若数列{ an }为等比数列,求证:数列{ cn }为等比数列.
(2)若数列{ cn }为等比数列,且 bn +1≥ bn ,求证:数列{ an }为等比数列.
相关课件
这是一份备战2025年高考数学精品课件第五章 第2讲 等差数列,共60页。PPT课件主要包含了一个常数,等差中项,规律总结,等差数列的单调性,等差数列的性质,最小公倍数,方法技巧,BCD,A15,B30等内容,欢迎下载使用。
这是一份备战2025年高考数学精品课件第五章 突破3 数列中的创新型问题,共32页。PPT课件主要包含了ABD,故选B等内容,欢迎下载使用。
这是一份2025年高考数学一轮复习-第五章 数列-第3讲 等比数列【课件】,共42页。PPT课件主要包含了必备知识自主排查,核心考点师生共研等内容,欢迎下载使用。


![《高考总复习》数学 第五章 第3讲 等比数列[配套课件]](http://jx-previews-01.oss-cn-hangzhou.aliyuncs.com/3/3/13744231/0/0.jpg?x-oss-process=image/resize,w_202)





