



所属成套资源:【艺考生专用】高考数学40天突破训练讲义(教师版+学生版)
专题20 三角函数的图象与性质-2025年新高考艺术生数学突破讲义
展开
这是一份专题20 三角函数的图象与性质-2025年新高考艺术生数学突破讲义,文件包含专题20三角函数的图象与性质原卷版docx、专题20三角函数的图象与性质解析版docx等2份学案配套教学资源,其中学案共39页, 欢迎下载使用。
1、“五点法”作图原理
在确定正弦函数的图像时,起关键作用的5个点是.
在确定余弦函数的图像时,起关键作用的5个点是.
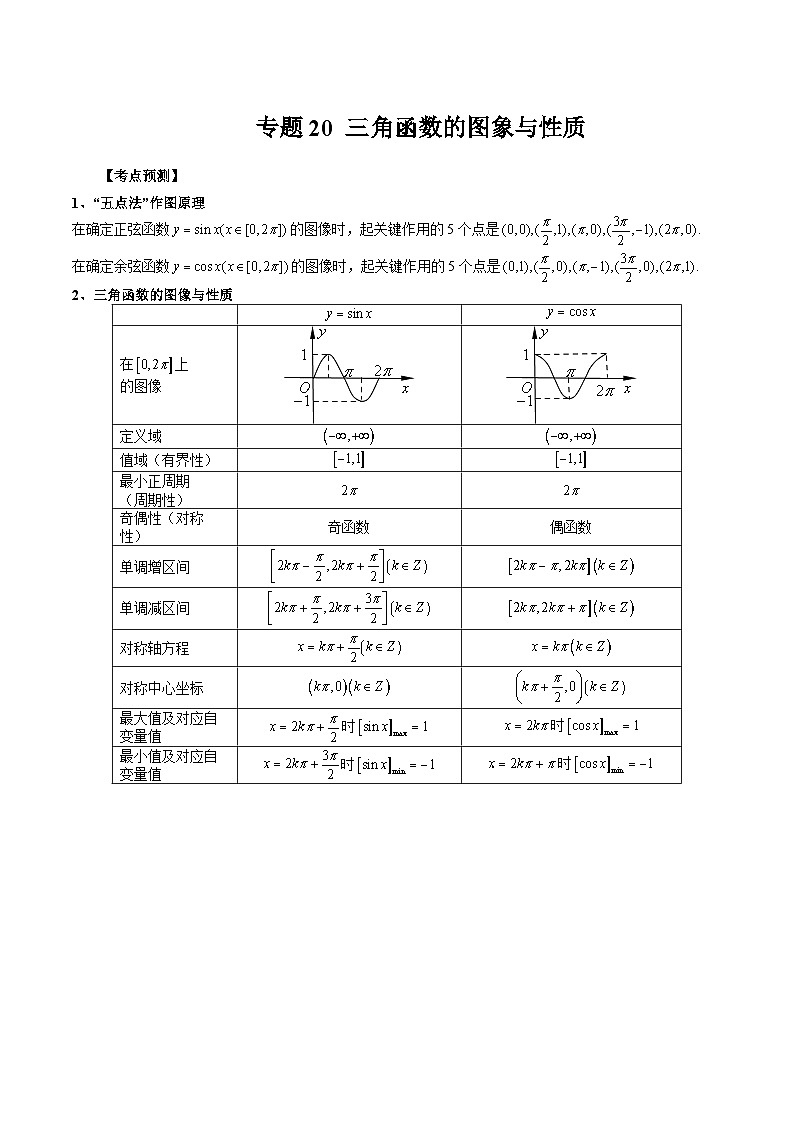
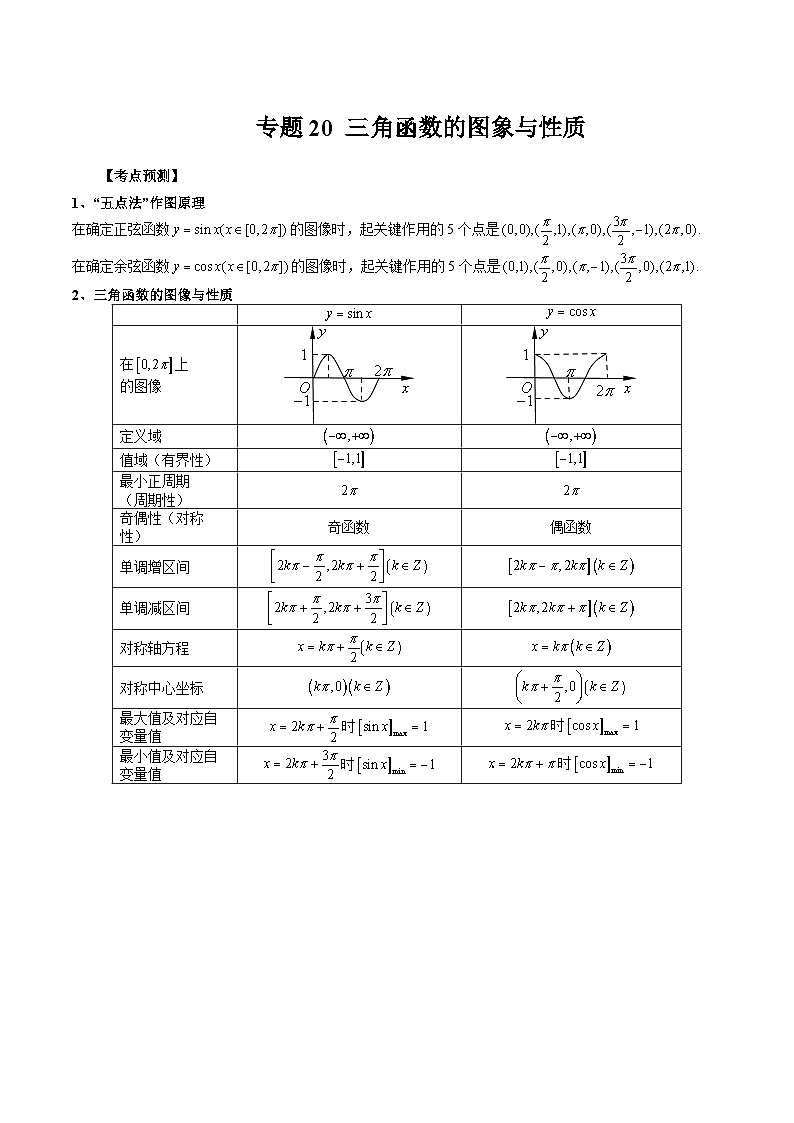
2、三角函数的图像与性质
3、与的图像与性质
(1)最小正周期:.
(2)定义域与值域:,的定义域为R,值域为[-A,A].
(3)最值
假设.
①对于,
②对于,
(4)对称轴与对称中心.
假设.
①对于,
②对于,
正、余弦曲线的对称轴是相应函数取最大(小)值的位置.正、余弦的对称中心是相应函数与轴交点的位置.
(5)单调性.
假设.
①对于,
②对于,
(6)平移与伸缩
(,)的图象,可以用下面的方法得到:
= 1 \* GB3 ①画出函数的图象;
= 2 \* GB3 ②把的图象向左()或向右()平移个单位长度,得到函数的图象;
= 3 \* GB3 ③把图象上各点的横坐标变为原来的倍(纵坐标不变),得到函数的图象;
= 4 \* GB3 ④把图象上各点的纵坐标变为原来的倍(横坐标不变),得到函数的图象.
【典例例题】
例1.(2024·陕西西安·一模)将函数的图象向左平移m()个单位,所得图象关于原点对称,则m的值可以是( ).
A.B.πC.D.
【答案】D
【解析】将函数的图象向左平移m个单位,
得的图象,
因为的图象关于原点对称,
所以,即,
当时,得,
使,,的整数不存在.
故选:D
例2.(2024·高三·江苏扬州·阶段练习)函数的最小正周期是( )
A.B.C.D.
【答案】B
【解析】,故最小正周期为.
故选:B
例3.(2024·高三·全国·阶段练习)函数在上没有最小值,则的取值范围是( )
A.B.C.D.
【答案】C
【解析】函数中,当时,,
由在上没有最小值,得,解得,
所以的取值范围是.
故选:C
例4.(2024·全国·二模)若函数的图象关于轴对称,则( )
A.B.C.D.
【答案】B
【解析】依题意,函数是偶函数,则,
即,而,所以.
故选:B
例5.(2024·四川·模拟预测)已知,若,则( )
A.B.C.D.
【答案】C
【解析】设,显然它定义域关于原点对称,
且,
所以为奇函数,
,则,
所以,.
故选:C.
例6.(2024·高三·江苏·专题练习)已知函数,把的图象向左平移个单位长度得到函数的图象,则( )
A.是偶函数
B.的图象关于直线对称
C.在上单调递增
D.不等式的解集为
【答案】B
【解析】A选项,,
由于的定义域为R,且,
故为奇函数,故A错误;
B选项,由选项A可知,故的图象的对称轴为,即,
令可得,即的图象关于直线对称,故B正确;
C选项,时,,其中在上不单调,
故在上不单调,故C错误;
D选项,,则,则,
故,D错误.
故选:B
例7.(2024·高三·安徽·阶段练习)已知函数的图象向右平移个单位长度后,得到函数的图象.若是偶函数,则为( )
A.B.C.D.
【答案】B
【解析】依题意,,
由是偶函数,得,,
而,则.
故选:B
例8.(2024·北京门头沟·一模)下列函数中, 既是奇函数又在上单调递增的是( )
A.B.
C.D.
【答案】D
【解析】对于A:定义域为,为非奇非偶函数,故A错误;
对于B:定义域为,为奇函数,但是函数在上单调递减,故B错误;
对于C:为奇函数,定义域为,但是函数在上不单调,故C错误;
对于D:令定义域为,且,
所以为奇函数,且当时,函数在上单调递增,故D正确.
故选:D
例9.(2024·山东淄博·一模)已知函数,则下列结论中正确的是( )
A.函数的最小正周期
B.函数的图象关于点中心对称
C.函数的图象关于直线对称
D.函数在区间上单调递增
【答案】D
【解析】对于A,函数的最小正周期,A错误;
对于B,由,得函数f(x)的图象不关于点对称,B错误;
对于C,由,得函数f(x)的图象不关于直线对称,C错误;
对于D,当时,,而正弦函数在上单调递增,
因此函数在区间上单调递增,D正确.
故选:D
例10.(2024·高三·全国·专题练习)若,则( )
A.B.C.0D.
【答案】C
【解析】由题意知的最小正周期为,
且,
故
,
故选:C
例11.(2024·高三·全国·专题练习)要得到余弦曲线y=cs x,只需将正弦曲线y=sin x( )
A.向左平移个单位长度
B.向右平移个单位长度
C.向左平移π个单位长度
D.向右平移π个单位长度
【答案】A
【解析】y=cs x=sin (x+),所以要得到余弦曲线y=cs x,只需将正弦曲线y=sin x向左平移个单位长度.
【考查意图】考查正弦函数与余弦函数图象的关系.
例12.(2024·高一·上海宝山·期末)函数的部分图象如图所示,则 .
【答案】/
【解析】由已知可得,,所以,所以,
所以.
又因为在处取得最大值,
所以有,
所以.
又因为,所以,
所以,
所以.
故答案为:.
例13.(2024·河北邯郸·三模)写出一个,使得函数的图象关于点对称,则可以为 .
【答案】(答案不唯一)
【解析】因为的图象关于点对称,
所以,则,故,
又,所以,,,…..
故答案为:(答案不唯一).
例14.(2024·高三·上海浦东新·期中)向量,令.
(1)求的周期:
(2)求时,的单调递增区间;
(3)求的值域.
【解析】(1),
所以的周期
(2)令,
即,,
当时,
当时,的单调递增区间是
(3)由,得,
故,所以的值域为
例15.(2024·高三·上海静安·期末)记,其中为实常数.
(1)求函数的最小正周期;
(2)若函数的图像经过点,求该函数在区间上的最大值和最小值.
【解析】(1).
∴函数的最小正周期为.
(2),
,则.
令,因为,则.
当或,即或时,.
当,即时,.
【过关测试】
一、单选题
1.(2024·湖北·二模)已知函数,,则函数的值域是( )
A.B.C.D.
【答案】B
【解析】由题意可知:
,
当时,则,所以
故选:B.
2.(2024·高三·云南·阶段练习)将函数的图象向右平移个单位后得到的图象,则时,的值域为( )
A.B.C.D.
【答案】C
【解析】由题意得,
所以当时,,.
故选:C
3.(2024·高三·陕西安康·阶段练习)若函数的最小正周期为,则的图象的一条对称轴方程为( )
A.B.C.D.
【答案】D
【解析】依题意,由,
得,所以的图象的一条对称轴为,
D选项正确,ABC选项错误.
故选:D
4.(2024·陕西榆林·二模)若函数的图象关于直线对称,则( )
A.B.C.D.
【答案】C
【解析】因为的图象关于直线对称,
所以,得,
因为,所以.
故选:C.
5.(2024·陕西咸阳·二模)已知函数,若时,函数的值域为( )
A.B.C.D.
【答案】A
【解析】,
因为,所以
则,
所以函数的值域为.
故选:A.
6.(2024·吉林延边·一模)将函数的图象向左平移个单位长度后得到曲线,若关于轴对称,则的最小值是( )
A.B.C.D.
【答案】B
【解析】结合题意可得,
因为曲线关于轴对称,所以,
解得,因为,所以当时,有最小值.
故选:B.
7.(2024·广东佛山·模拟预测)将函数的图象向右平移个单位长度后得到函数的图像,且函数是偶函数,则的最小值是( )
A.B.C.D.E.均不是
【答案】A
【解析】由题意知,()
又因为为偶函数,所以关于轴对称.
所以,,解得,,
又,所以当时,取得最小值为.
故选:A.
8.(2024·四川泸州·二模)已知函数的最小正周期为,且的图象关于直线对称,则b的值为( )
A.B.C.D.1
【答案】D
【解析】因为(其中),
又的最小正周期为,,所以,则,
所以,
又函数的图象关于直线对称,
所以,
所以,解得.
故选:D
9.(2024·四川泸州·二模)已知函数的图象关于直线对称,则的值为( )
A.B.C.D.1
【答案】D
【解析】因为(其中),
又函数的图象关于直线对称,
所以,
所以,解得.
故选:D
10.(2024·四川南充·二模)将函数的图象向左平移个单位长度,得到函数的图象,则曲线与直线的所有交点中,相邻交点距离的最小值为( )
A.B.C.D.
【答案】A
【解析】函数的图象向左平移个单位长度,
得到函数的图象,,
令,,
则,,或,,
即,,或,,
可得,,,,
,,,,
相邻交点距离的最小值为.
故选:A.
11.(2024·陕西渭南·模拟预测)将函数的图象向左平移个单位长度后得到函数的图象,则的图象的一条对称轴为( )
A.直线B.直线C.直线D.直线
【答案】D
【解析】由题意可得,
令,则,
当时,有,其余选项均不符合.
故选:D.
二、多选题
12.(2024·云南昆明·一模)已知函数,若,则的值可以为( )
A.B.C.D.
【答案】BD
【解析】令或,,
故或,,
故,
取和可得或,
故的值可以为或,
故选:BD
13.(2024·山东枣庄·一模)已知函数,则( )
A.的最大值为2
B.在上单调递增
C.在上有2个零点
D.把的图象向左平移个单位长度,得到的图象关于原点对称
【答案】AC
【解析】函数
.
选项A:,,故最大值为2,A正确;
选项B:时,,不单调递增,故B错误;
选项C:时,,可知当以及时,即以及时,在上有2个零点,故C正确;
选项D:的图象向左平移个单位长度,得到,不关于原点对称,故D错误.
故选:AC.
14.(2024·全国·模拟预测)已知函数,则下列结论正确的是( )
A.的图象关于点对称
B.若是偶函数,则,
C.在区间上的值域为
D.的图象关于直线对称
【答案】ABD
【解析】对A:,故A正确.
对B:因为是偶函数,
所以,,即,,故B正确.
对C:当时,,,
所以,故C错误.
对D:当时,,故D正确
15.(2024·河南南阳·一模)已知函数的部分图像如图所示、则下列结论正确的是( )
A.在上有两个极值点B.
C.函数的图象关于轴对称D.若,则的最小值为
【答案】AC
【解析】由题图知,
所以,
由图象可知在时取得极大值,则在时取得极小值,
所以上有两个极值点,A正确;
又,所以,
所以.
因为,所以令,即.
所以.所以,B错误;
因为函数的周期为,将图象上的所有点沿轴向右平移个单位长度后得到的图象,为偶函数,
所以函数的图象关于轴对称,C正确;
若,则的最小值为错误.
故选:.
16.(2024·贵州毕节·模拟预测)已知函数,下列说法正确的是( )
A.的周期为
B.函数为偶函数
C.函数的图像关于直线对称
D.函数在上的最小值为
【答案】AC
【解析】对于A,的周期,故A正确;
对于B,令,
因为,所以函数为奇函数,
即数为奇函数,故B错误;
对于C,因为,
所以函数的图像关于直线对称,故C正确;
对于D,由,得,
所以函数在上的最小值为,故D错误.
故选:AC.
17.(2024·高三·全国·专题练习)已知函数,则下列描述正确的是( )
A.函数的最小正周期为
B.是函数图象的一个对称轴
C.是函数图象的一个对称中心
D.若函数的图象向左平移个单位长度可得函数的图象,则为奇函数
【答案】ACD
【解析】函数的最小正周期,故A正确;
,所以关于对称,故B错误;
,所以是函数图象的一个对称中心,故C正确;
根据题意,
则,所以为奇函数,故D正确.
故选:ACD.
18.(2024·浙江·二模)关于函数,下列说法正确的是( )
A.最小正周期为B.关于点中心对称
C.最大值为D.在区间上单调递减
【答案】BC
【解析】,
,
函数的最小正周期,故A错误;
,所以函数图象关于点中心对称,故B正确;
,所以函数的最大值为,故C正确;
由,,函数在区间单调递增,
所以函数在区间上单调递增,故D错误.
故选:BC
19.(2024·福建莆田·二模)已知函数,则( )
A.
B.的最大值为1
C.在上单调递增
D.将函数的图象向右平移个单位长度后与的图象重合
【答案】AD
【解析】对于AB,,,故A对B错;
当,故C错误;
将函数的图象向右平移个单位长度后的图象所对应的函数表达式为,故D正确.
故选:AD.
20.(2024·河北·模拟预测)要得到函数的图象,可将函数的图象( )
A.向左平移个单位长度,再将所得图象上所有点的纵坐标不变,横坐标变为原来的2倍
B.向左平移个单位长度,再将所得图象上所有点的纵坐标不变,横坐标变为原来的
C.纵坐标不变,横坐标变为原来的,再将所得图象上所有点向左平移个单位长度
D.纵坐标不变,横坐标变为原来的2倍,再将所得图象上所有点向左平移个单位长度
【答案】BC
【解析】对于A,所得解析式为,A错误;
对于B,所得解析式为,B正确;
对于C,所得解析式为,C正确;
对于D,所得解析式为,D错误.
故选:BC
21.(2024·浙江·模拟预测)为了得到函数的图象,只要把函数图象上所有的点( )
A.向左平移个单位长度B.向右平移个单位长度
C.向左平移个单位长度D.向右平移个单位长度
【答案】AD
【解析】把函数图象上所有的点向左平移个单位长度,
可得函数的图象,A正确;
把函数图象上所有的点向右平移个单位长度,
可得函数的图象,B错误;
把函数图象上所有的点向左平移个单位长度,
可得函数的图象,C错误;
把函数图象上所有的点向右平移个单位长度,
可得函数的图象,D正确;
故选:AD.
三、填空题
22.(2024·高三·江苏苏州·阶段练习)已知 ,则的最小正周期为 , .
【答案】
【解析】,
其最小正周期,
因为
故.
故答案为:;.
23.(2024·北京门头沟·一模)若函数 的最大值为 , 则 , .
【答案】 1
【解析】,
由最大值为,,则,
所以,
所以,
故答案为:;
24.(2024·重庆·模拟预测)设函数在上为减函数,如果 ,,,那么 . (写出 一个即可)
【答案】(答案不唯一)
【解析】由已知函数在上单调递减,
又在上单调递减,
可令,符合题意.
故答案为:(答案不唯一).
25.(2024·高三·重庆永川·阶段练习)函数(其中,,)的图象如图所示,则函数的解析式为 ,若将该函数的图象上的各点的横坐标伸长为原来的3倍(纵坐标不变)得到函数,则 .
【答案】
【解析】由图象易知,,图象过点,即,,,所以,
又图象过点,即,
所以,解得,
所以函数的解析式为,
可得,
故,
故答案为:;.
26.(2024·高三·北京海淀·期中)已知函数的部分图象如图所示.
①函数的最小正周期为 ;
②将函数的图象向右平移个单位长度,得到函数的图象.若函数为奇函数,则的最小值是 .
【答案】
【解析】空1:由图可知,即
空2:,即,
则,又过点,
所以,即,
又在原图增区间上,所以可取,
所以,
向右平移个单位可得,
又为奇函数,所以,
即,
又,
所以.
故答案为:;.
27.(2024·高三·上海嘉定·期中)若将函数向右平移个单位后其图像关于轴对称,则 .
【答案】
【解析】易知函数向右平移个单位后得函数,
此时函数关于轴对称,则,
又,所以时,.
故答案为:.
28.(2024·高三·全国·对口高考)为了得到函数的图象,只需把函数的图象向 长度单位.
【答案】向右平移个
【解析】,,
因此,只需将函数的图象向右平移个长度单位即:
.
故答案为:向右平移个.
四、解答题
29.(2024·黑龙江·二模)已知向量,,且函数在上的最大值为.
(1)求常数的值;
(2)求函数的单调递减区间.
【解析】(1),
,,解得:.
(2)由(1)知:,
令,解得:,
的单调递减区间为.
30.(2024·高三·山西吕梁·阶段练习)已知函数,将图象上每一点的横坐标缩短为原来的,再将所得图象向上平移1个单位长度得到函数的图象.
(1)求图象的对称中心;
(2)若函数在上没有最小值,求实数m的取值范围.
【解析】(1)根据题意,,
由,得,,
所以函数图象的对称中心为,.
(2)由(1)知:,
因为,所以,
要使在上没有最小值,
则,解得,即实数的取值范围为.
31.(2024·高三·宁夏银川·阶段练习)已知函数的两条相邻对称轴之间距离为.
(1)求的值;
(2)将函数图象向右平移个单位长度得到的图象,若,,求的值.
【解析】(1)
,
由题意得,解得;
(2),
故,
,故,
因为,所以,
因为,所以,
故,
所以
.
32.(2024·高三·湖南长沙·阶段练习)已知向量
(1)若⊥,求的值;
(2)记,将函数的图象向右平移个单位,再向下平移1个单位得到函数图象,求函数在上的最小值.
【解析】(1)⊥,故,
即,
故有或,
当时,又
,
当,即,
又,故,
或;
(2),
由题意知,
,
∴,
由于在上单调递增,在上单调递减,
又,,
故在上的最小值为.
33.(2024·高三·四川内江·阶段练习)已知函数.
(1)判断函数在上的单调性;
(2)将函数的图象向右平移个周期后得到函数的图象,求函数在区间上的值域.
【解析】(1)原式,
令,解得,
又因为,可得函数的递增区间为,递减区间为,
所以函数在单调递增,在单调递减.
(2)因为,周期,
向右平移个周期后得到函数的图象,则,
因为,
所以
在上
的图像
定义域
值域(有界性)
最小正周期
(周期性)
奇偶性(对称性)
奇函数
偶函数
单调增区间
单调减区间
对称轴方程
对称中心坐标
最大值及对应自变量值
时
时
最小值及对应自变量值
时
时
函数
正切函数
图像
定义域
值域
周期性
奇偶性
奇函数,图像关于原点对称
单调性
在上是单调增函数
对称轴
无
对称中心
相关学案
这是一份专题41 数列求和 -2025年新高考艺术生数学突破讲义,文件包含专题41数列求和原卷版docx、专题41数列求和解析版docx等2份学案配套教学资源,其中学案共31页, 欢迎下载使用。
这是一份专题40 数列通项 -2025年新高考艺术生数学突破讲义,文件包含专题40数列通项原卷版docx、专题40数列通项解析版docx等2份学案配套教学资源,其中学案共29页, 欢迎下载使用。
这是一份专题29 排列组合 -2025年新高考艺术生数学突破讲义,文件包含专题29排列组合原卷版docx、专题29排列组合解析版docx等2份学案配套教学资源,其中学案共24页, 欢迎下载使用。









