第27章 圆 华师大版九年级数学下册复习课课件

这是一份第27章 圆 华师大版九年级数学下册复习课课件，共37页。
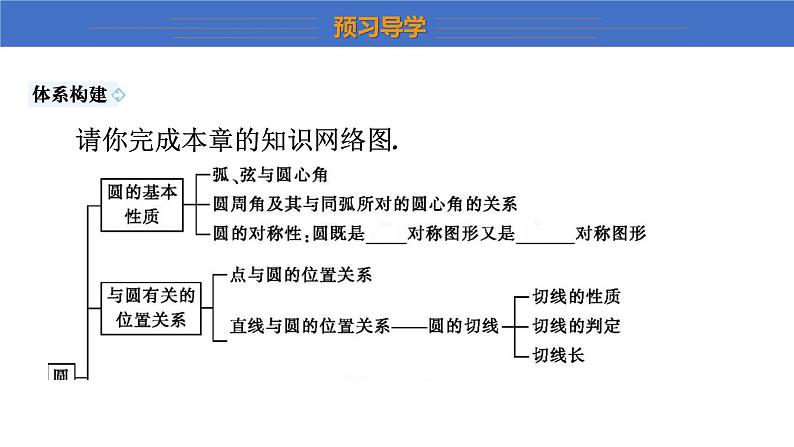
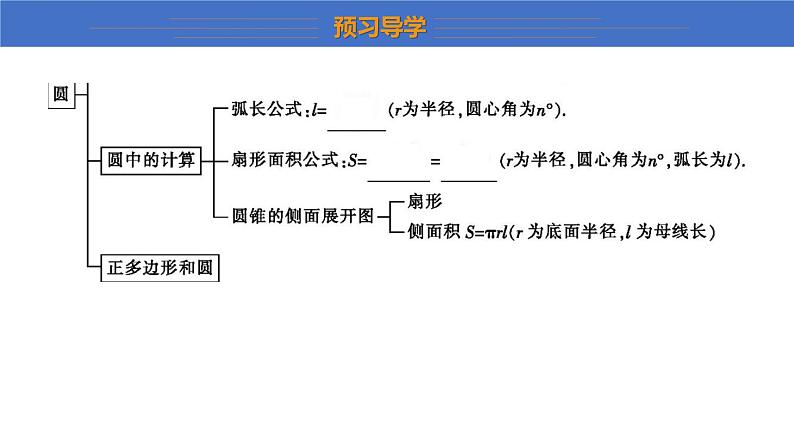
第27章　圆第27章　复习课 1.知道圆的有关概念，认识圆心角、弧、弦之间的相等关系的定理，知道圆周角和圆心角的关系定理，垂径定理.2.知道点和圆、直线与圆的位置关系，熟记切线的性质定理与判定定理，能判定一条直线是否为圆的切线，会过圆上一点画圆的切线，知道切线长定理.3.进一步认识正多边形和圆的关系和正多边形的有关计算.熟记弧长和扇形面积公式；知道圆锥的侧面展开图并能熟练进行圆锥的侧面积和全面积的计算.◎重点:系统地归纳总结本章知识内容.◎难点:使所学的知识结构化. 经过一段时间的学习，《圆》这一章的内容学完了，今天我们这节课的主要任务就是回顾一下这期间所学的内容，将其整理归纳，使之结构化. 请你完成本章的知识网络图. 　　1.圆心角、弦、弧之间的关系:(1)在同一个圆中，如果圆心角相等，那么它们所对的弧　相等　，所对的弦　相等　. (2)在同一个圆中，如果弧相等，那么它们所对的圆心角　相等　，所对的弦　相等　. (3)在同一个圆中，如果弦相等，那么它们所对的圆心角　相等　，所对的弧　相等　. 相等相等相等相等相等相等2.垂径定理:垂直于弦的直径平分这条弦，并且平分这条弦所对的两条弧.推论:平分弦(不是直径)的直径　垂直于　这条弦，并且　平分　这条弦所对的两条弧； 平分弧的直径　垂直平分　这条弧所对的弦. 3.　半圆　或　直径　所对的圆周角相等，都等于90°(直角). 垂直于平分垂直平分半圆直径4.圆周角定理:在同圆或等圆中，同弧或等弧所对的圆周角　相等　，都等于该弧所对的圆心角的　一半　；相等的圆周角所对的弧　相等　. 推论1:90°的圆周角所对的弦是　直径　. 推论2:圆内接四边形的对角　互补　. 5.点与圆的位置关系:点P在☉O上⇔OP　＝　r；点P在☉O内⇔OP　＜　r；点P在☉O外⇔OP　＞　r. 相等一半相等直径互补＝＜＞6.　不在同一条直线上　的三个点确定一个圆. 不在同一条直线上7.(1)经过三角形三个顶点的圆就是这个三角形的外接圆.三角形外接圆的圆心叫做这个三角形的外心.三角形的外心就是三角形三条边的垂直平分线的交点.(2)与三角形各边都相切的圆叫做这个三角形的内切圆.三角形的内切圆的圆心叫做这个三角形的内心.三角形的内心就是三角形三条角平分线的交点.8.直线与圆的位置关系:设圆的半径为r，圆心O到直线l的距离为d，则直线l与☉O相离⇔d　＞　r；直线l与☉O相切⇔d　＝　r；直线l与☉O相交⇔d　＜　r. 9.切线的判定定理:经过圆的半径的　外端　且　垂直于　这条半径的直线是圆的切线. 10.切线的性质定理:圆的切线　垂直　于经过切点的半径. ＞＝＜外端垂直于垂直11.切线长定理:过圆外一点所画的圆的两条切线，它们的切线长　相等　.这一点和圆心的连线　平分　这两条切线的夹角. 相等平分·导学建议·预习导学部分可由教师提问、学生回答的形式完成，建议学生在课前对不熟悉的知识自己复习，预习导学部分建议教师用10分钟的时间完成. 圆的基本性质1.如图，AB是☉O的直径，点C、D是☉O上的点，若∠CAB＝25°，则∠ADC＝　65°　. 65°2.一根排水管的截面如图所示，已知排水管的半径OA＝1 m，水面宽AB＝1.2 m，某天下雨后，水管水面上升了0.2 m，则此时排水管水面宽CD等于　1.6　m. 1.6方法归纳交流　垂径定理是计算圆中线段长的主要工具，在圆中，过圆心作弦的垂线，连接圆心和弦的两个端点，再由“半径、弦长的一半、弦心距”组成　直角　三角形，结合　勾股　定理进行相关计算. 直角勾股    方法归纳交流　在同圆或等圆中，圆心角、弧、弦之间的相等关系可以相互转化，知道其中一组量相等，则它们所对应的其他各组量也　相等　. 相等 与圆有关的位置关系4.已知☉O的半径是4，OP＝3，则点P与☉O的位置关系是(　A　)A5.如图，两个同心圆，大圆的半径为5，小圆的半径为3，若大圆的弦AB与小圆有公共点，则弦AB的取值范围是(　A　)A·导学建议·本题是易错题，在此可提醒学生注意:直线与圆有公共点隐含着两层含义:①直线与圆有且只有一个公共点，即直线与圆相切；②直线与圆有两个公共点，即直线与圆相交.　　6.如图，已知Rt△ABC的斜边AB＝8 cm，AC＝4 cm.(1)以点C为圆心作圆，当半径为多长时，直线AB与☉C相切？(2)以C为圆心，分别以2 cm和4 cm为半径作两个圆，则这两个圆与直线AB分别有怎样的位置关系？解:(1)如图，过点C作CD⊥AB，垂足为D.      方法归纳交流　判断点和圆、直线和圆的位置关系，常转化为两点之间的距离、　圆心到直线的距离　，与半径比较大小来解决. 圆心到直线的距离 切线长定理、切线的性质和判定7.如图，AB是☉O的弦，AC是☉O的切线，A为切点，BC经过圆心，若∠C＝56°，则∠ABC的度数为　17°　. 17°8.如图，AB是☉O的直径，点C为☉O外一点，CA，CD是☉O的切线，A，D为切点，连接BD，AD.若∠ACD＝30°，则∠DBA的大小是(　D　)D9.如图，已知BC是☉O的直径，AC切☉O于点C，AB交☉O于点D，E为AC的中点，连接DE.(1)若AD＝DB，OC＝5，求切线AC的长.(2)求证:ED是☉O的切线.解:(1)连接CD.∵BC是☉O的直径，∴∠BDC＝90°，即CD⊥AB，∵AD＝DB，∴AC＝BC＝2OC＝10. 方法归纳交流　在涉及切线问题时，常连接过　切点　的半径，要想证明一条直线是圆的切线，常常需要做辅助线.若已知直线过圆上某一点，则作出过这一点的半径，证明直线　垂直　于半径；若直线与圆的的公共点没有确定，则应过圆心作直线的垂线，证明圆心到直线的距离等于　半径　. 切点垂直半径 三角形的内切圆与外接圆10.在Rt△ABC中，∠C＝90°，AC＝3，AB＝5，则它的内切圆与外接圆的半径分别为(　C　)C　　11.如图，AC，BE是☉O的直径，弦AD与BE交于点F，则下列三角形中，外心不是点O的是(　B　)B    圆中的计算问题12.将直径为60 cm的圆形铁皮，做成三个相同的圆锥容器的侧面(不浪费材料，不计接缝处的材料损耗)，那么每个圆锥容器的底面半径为(　A　)A π