初中数学人教版（2024）九年级上册25.3 用频率估计概率教学课件ppt

这是一份初中数学人教版（2024）九年级上册25.3 用频率估计概率教学课件ppt，共25页。PPT课件主要包含了正面向上，反面向上，都是05，结果保留小数点后两位，由图你还能发现什么，判断正误，确定的常数理论值，与试验次数的变化有关，钉尖向上，钉尖向下等内容，欢迎下载使用。
1.能够通过随机试验，获得事件发生的频率；知道通过大量重复试验，可以用频率估计概率；2.经历利用频率估计概率的过程，让学生了解频率和概率的区别与联系，发展利用频率的集中趋势估计概率的能力；3.经历抛掷硬币试验和投图钉试验，对数据进行收集、整理、描述与分析，体验频率的随机性与规律性，了解用频率估计概率的合理性和必要性，培养随机观念；4.通过实验培养学生的数据处理、分析能力以及合作探究精神.
抛掷一枚质地均匀的硬币，硬币落地后会出现哪些可能的结果？
“正面向上”和“反面向上”的概率分别是多少？
抛掷一枚硬币50次，一定会有25次“正面向上”和25次“反面向上”吗？
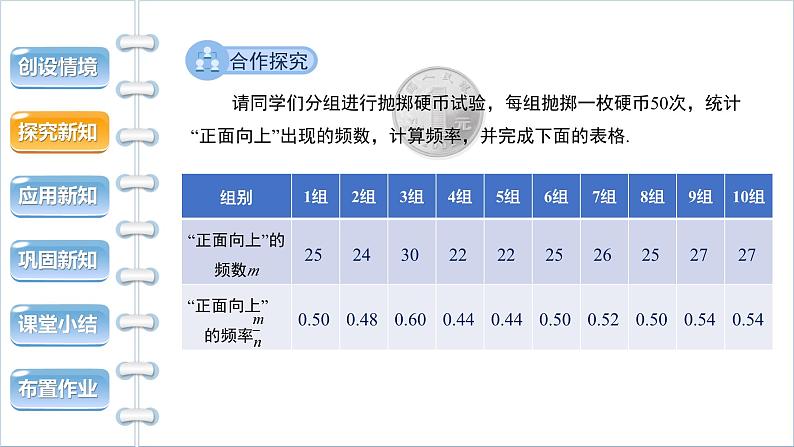
请同学们分组进行抛掷硬币试验，每组抛掷一枚硬币50次，统计“正面向上”出现的频数，计算频率，并完成下面的表格.
根据表中的数据，在下图中标注出对应的点.
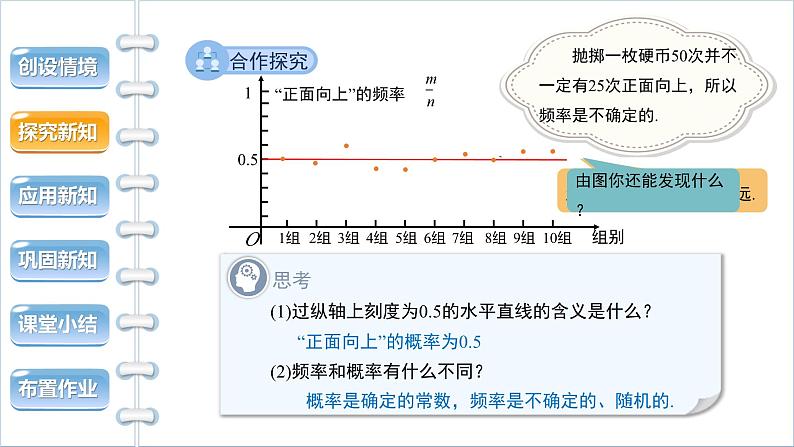
(1)过纵轴上刻度为0.5的水平直线的含义是什么？
(2)频率和概率有什么不同？
“正面向上”的概率为0.5
概率是确定的常数，频率是不确定的、随机的.
大部分组的频率离0.5不远.
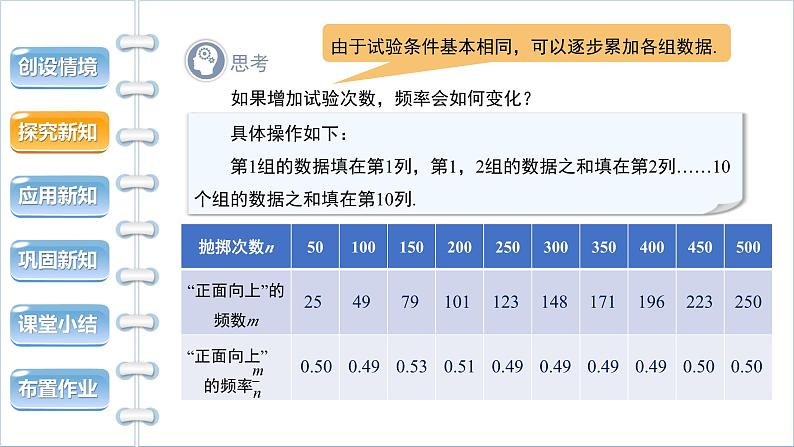
如果增加试验次数，频率会如何变化？
具体操作如下： 第1组的数据填在第1列，第1，2组的数据之和填在第2列……10个组的数据之和填在第10列.
由于试验条件基本相同，可以逐步累加各组数据.
根据表中的数据，在下图中标注出对应的点.
随着试验次数的增多，“正面向上”的频率有什么规律？
“正面向上”的频率在0.5左右摆动，随着抛掷次数的增加，在0.5左右摆动的幅度越来越小.
历史上，有些人曾做过成千上万次抛掷硬币的试验，一些试验结果如下表，由表观察“正面向上”的频率的变化趋势是什么？
随着抛掷次数的增加，频率呈现出一定的稳定性：在0.5附近摆动的幅度越来越小.
我们称“正面向上”的频率稳定于0.5.它与用列举法得出的“正面向上”的概率是同一个数值.
对一般的随机事件，在做大量重复试验时，随着试验次数的增加，一个事件出现的频率，总在一个固定数的附近摆动，显示出一定的稳定性.
我们可以通过大量重复试验，用一个随机事件发生的 去估计它的 .
雅各布·伯努利1654年出生于瑞士巴塞尔，1705年卒于同地.最初遵从父亲的意见学神学，后来兴趣转向数学.他的遗著《猜度术》于1713年出版，书中对频率的稳定性规律进行了严格的证明，阐述了“频率稳定于概率”.
雅各布·伯努利概率论的先驱之一
(1)连续掷一枚质地均匀硬币10次，结果10次全部是正面，则正面向上的概率是1.
(2)小明掷硬币10000次，则正面向上的频率在0.5附近.
(3)某彩票的中奖率是 ，那么买1000张彩票就一定能中奖.
频率与概率的区别与联系
不确定的数（试验值或使用的统计值）
与试验次数的变化无关
与试验人、试验时间、试验地点有关
与试验人、试验时间、试验地点无关
试验次数越多，频率越趋向于概率
【例】从一定高度抛掷一枚图钉，估计出“钉尖向上”的概率.(要求：设计一个试验，用频率估计概率)
解：试验参考过程如下： 每组同学投一枚图钉50次，第1组的数据填在第1列，第1，2组的数据之和填在第2列……10个组的数据之和填在第10列.
尽可能保证试验条件相同
根据表格数据在下图中标注点.
频率稳定在0.56附近，所以，“钉尖向上”的概率为0.56.
能用列举法求上述随机事件的概率吗？
列举法求概率仅适用于“各种结果出现的可能性相等”的随机事件，用频率估计概率不受这个条件限制.
1.在大量重复试验中，关于随机事件发生的频率与概率，下列说法正确的是( ) A.频率就是概率 B.频率与试验次数无关 C.概率是随机的，与频率无关 D.随着试验次数的增加，频率一般会越来越接近概率
2.下表记录了一名球员在罚球线上投篮的结果.
(1)计算投中频率(结果保留小数点后两位)；(2)这名球员投篮一次，投中的概率约是多少(结果保留小数点后一位) ？
解：(2)投中的概率约是0.5.
3. 如图显示了用计算机模拟随机投掷一枚图钉的某次试验的结果.下面有三个推断，其中合理的是( )① 当投掷次数是500时，计算机记录“钉尖向上”的次数是308，所以“钉尖向上”的概率是0.616；② 随着试验次数的增加，“钉尖向上”的频率总在0.618附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是0.618； ③ 若再次用计算机模拟此试验，则当投掷次数为1 000时，“钉尖向上”的概率一定是① B.② C.①② D.①③
频率与概率的区别与联系：
我们可以通过大量重复试验，用一个随机事件发生的频率去估计它的概率.
概率是确定的常数，频率是不确定的、随机的，受试验条件影响.试验次数越多，频率越趋向于概率.
教科书第144页练习第2题第147页习题25.3第3题