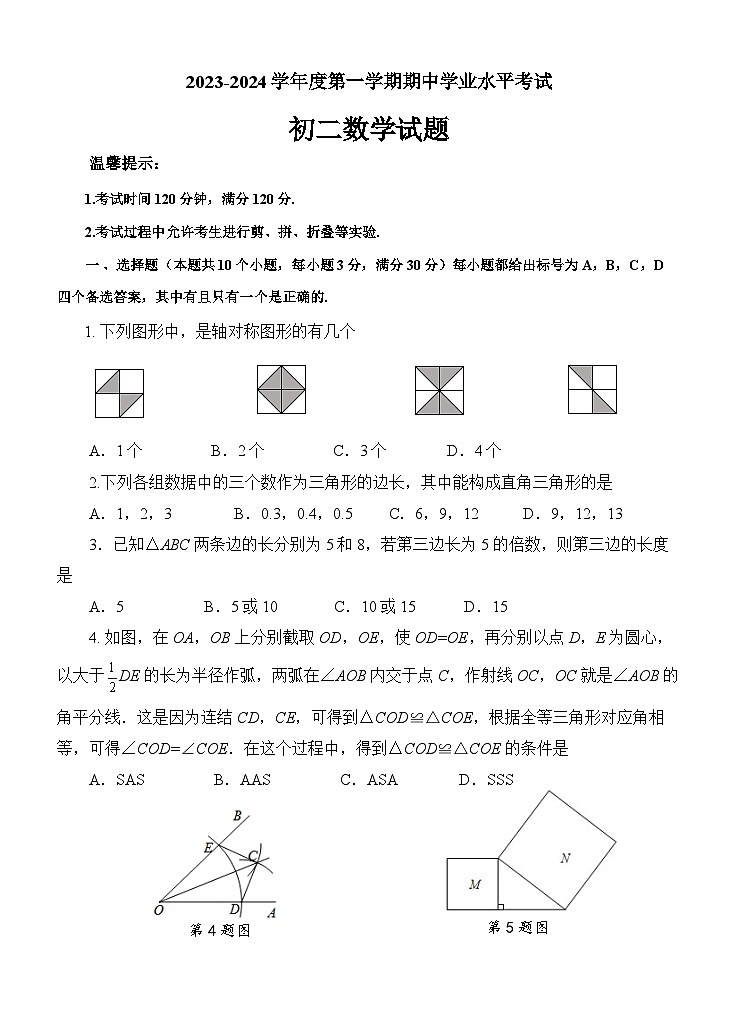

2023-2024学年山东省烟台市福山区七年级(上)期中数学试卷(五四学制)
展开
这是一份2023-2024学年山东省烟台市福山区七年级(上)期中数学试卷(五四学制),共14页。试卷主要包含了3,0, 下列三角形是直角三角形的是等内容,欢迎下载使用。
温馨提示:
1.考试时间120分钟,满分120分.
2.考试过程中允许考生进行剪、拼、折叠等实验.
一 、选择题(本题共10个小题,每小题3分,满分30分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1. 下列图形中,是轴对称图形的有几个
A.1个 B.2个 C.3个 D.4个
2.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是
A.1,2,3 B.0.3,0.4,0.5 C.6,9,12 D.9,12,13
3.已知△ABC两条边的长分别为5和8,若第三边长为5的倍数,则第三边的长度是
A.5 B.5或10 C.10或15 D.15
4. 如图,在OA,OB上分别截取OD,OE,使OD=OE,再分别以点D,E为圆心,以大于DE的长为半径作弧,两弧在∠AOB内交于点C,作射线OC,OC就是∠AOB的角平分线.这是因为连结CD,CE,可得到△COD≌△COE,根据全等三角形对应角相等,可得∠COD=∠COE.在这个过程中,得到△COD≌△COE的条件是
第4题图
第5题图
A.SAS B.AAS C.ASA D.SSS
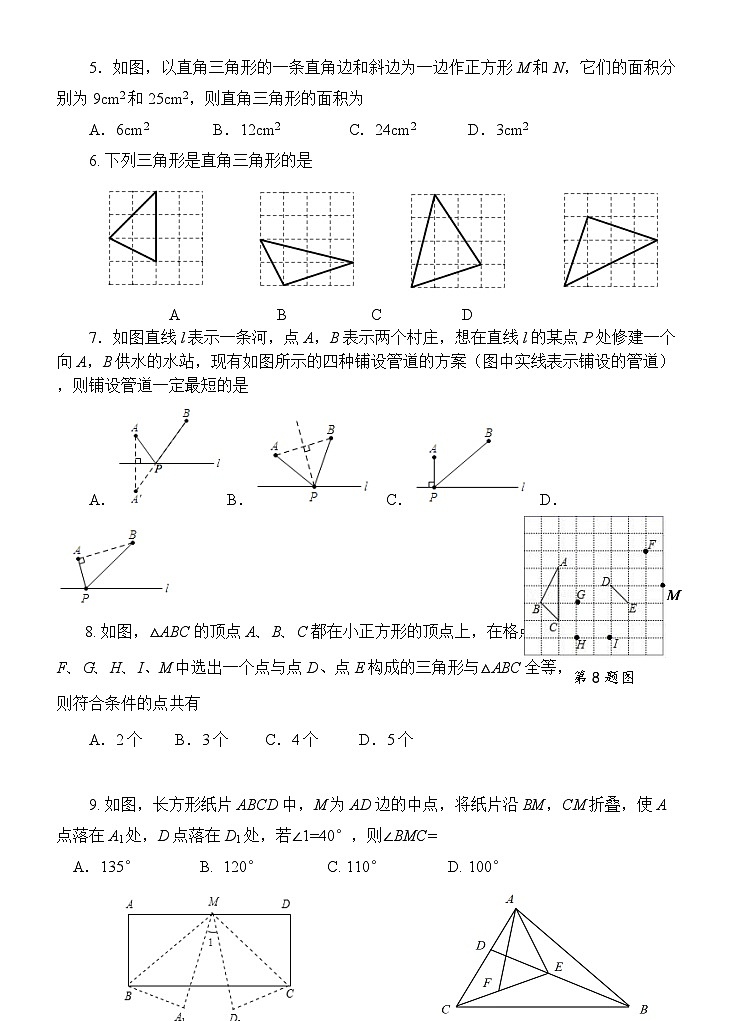
5.如图,以直角三角形的一条直角边和斜边为一边作正方形M和N,它们的面积分别为9cm2和25cm2,则直角三角形的面积为
A.6cm2 B.12cm2 C.24cm2 D.3cm2
6. 下列三角形是直角三角形的是
A B C D
7.如图直线l表示一条河,点A,B表示两个村庄,想在直线l的某点P处修建一个向A,B供水的水站,现有如图所示的四种铺设管道的方案(图中实线表示铺设的管道),则铺设管道一定最短的是
第8题图
M
A. B. C. D.
8. 如图,△ABC的顶点A、B、C都在小正方形的顶点上,在格点
F、G、H、I、M中选出一个点与点D、点E构成的三角形与△ABC全等,
则符合条件的点共有
A.2个 B.3个 C.4个 D.5个
如图,长方形纸片ABCD中,M为AD边的中点,将纸片沿BM,CM折叠,使A点落在A1处,D点落在D1处,若∠1=40°,则∠BMC=
A.135° B. 120° C. 110° D. 100°
第9题图
第10题图
10.如图,BD是△ABC的中线,点E,F分别为BD,CE的中点.若△AEF的面积为4,则△ABC的面积是
A. B. C. D.
二、填空题(本题共6个小题,每小题3分,满分18分)
11. 如图,要测池塘两端A,B的距离,小明先在地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,由△ABC和△DEC全等得到DE=AB.
那么判定其全等的依据是 (用三个字母表示).
第12题图
第11题图
12. 如图,在方格纸中,随机选择标有序号 = 1 \* GB3 \* MERGEFORMAT ① = 2 \* GB3 \* MERGEFORMAT ② = 3 \* GB3 \* MERGEFORMAT ③ = 4 \* GB3 \* MERGEFORMAT ④ = 5 \* GB3 \* MERGEFORMAT ⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的小正方形为 (填序号).
13. 如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,绳子BC的长为17米,后来船到
第13题图
第14题图
达点D位置,此时绳子CD长为10米,则船向岸边移动了 米.
如图,把△ABC沿线段DE折叠,使点A落在点F处,BC∥DE,若∠A+∠B=100°,则∠FEC= .
第15题图
第16题图
15. 如图,已知长方体的长AC=2cm,宽BC=1cm,高AA′=4cm.一只蚂蚁如果沿长方体的表面从A点爬到B′点,最短路程是 cm.
如图,∠AOB=30°,点P是∠AOB内的一定点,且OP=6,若点M,N分别是射线OA,OB上异于点O的动点,则△PMN周长的最小值是 .
第13题图
三、解答题(本大题共9个小题,满分72分,解答题要写出必要的计算步骤或文字说明或说理过程)
17.(本题满分6分)
如图,长方形ABCD沿AE折叠,使点D落在BC边上的F点处,若AD=5,AB=3,求EF的长度.
18.(本题满分6分)
已知:如图,在△ABC中,.
用圆规、直尺作图,不写作法,但要保留作图痕迹.
求作:点D,使点D在AC边上,且AD=BD.
求作:△PEF, 使PE=AB. , EF=BC.
19.(本题满分6分)
如图,在直角坐标系中,△ABC的三个顶点的坐标分别为
A(1,5),B(1,-2),C(4,0)
(1)请在图中画出△ABC关于y轴对称的△A'B'C ';
(2)求△ABC的面积;
(3)在y轴上画出点P,使PA+PC的值最小,保留画图痕迹.
20.(本题满分8分)
如图,△ABC中,为边上的一点,,以线段为边作△ADE,使得,.求证:.
21.(本题满分8分)
《九章算术》是我国古代重要的数学著作之一,其中记载了一道“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?译为:一根直立地面的竹子,原来高一丈,自A处折断,其竹梢B恰好抵地,抵地处与原竹子底部C距离三尺,问直立处还有多高的竹子?(一丈=十尺)
22.(本题满分8分)
如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D.
(1)求∠ADC的度数;
(2)试说明:DC=2DB.
23.(本题满分8分)
B
H
A
C
如图,在一条河的北侧有一村庄C,河边原有两个取水点A,B,其中,因规划建设,点C到点A段暂时封闭施工,为方便村民取水,决定在河边新建一个取水点H,(A,H,B在一条直线上),并修一条路CH.测得千米,千米,千米.
(1)请判断CH是否为从村庄C到河边的最近路?
并说明理由.
(2)求原来的路线AC的长.
24.(本题满分10分)
A
B
D
C
E
1
2
3
4
如图,在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠1=∠2,连接CE.
(1)请判断∠3与∠4相等吗?并说明理由.
(2)若∠1=32°,求∠ECD的度数.
25.(本题满分12分)
【问题探究】
如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥m于点D,CE⊥m于点E,试说明:△ABD≌△CAE.
【变式拓展】
如图②,在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,试探究线段DE、BD、CE三者之间的数量关系,并说明理由.
图1
图2
相关试卷
这是一份2024-2025学年山东省烟台市福山区(五四制)九年级(上)期中数学试卷(解析版),共21页。试卷主要包含了单选题,解答题等内容,欢迎下载使用。
这是一份2023-2024学年山东省烟台市芝罘区七年级(上)期末数学试卷(五四学制),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2023-2024学年山东省烟台市福山区八年级(上)期末数学试卷(五四学制)(含解析),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









