高中数学沪教版（2020）必修第二册7.3 函数y= Asin(ωx + φ)的图像集体备课ppt课件

这是一份高中数学沪教版（2020）必修第二册7.3 函数y= Asin(ωx + φ)的图像集体备课ppt课件，共18页。PPT课件主要包含了答案C等内容，欢迎下载使用。
在现实生活中，我们知道钟表分针的转动具有周期现象．怎样用函数来描述这种周期现象呢？
如图 ，假设分针的旋转中心到针尖末端的长度为A， 设 分时，分针针尖指向点 ，随着t的增加，分针沿顺时针方向走动，设经过t分钟，针尖指向点P
以分针的旋转中心为坐标原点，建立如图 所示的平面直角坐标系．设指向点p的针尖末端对应的点的纵坐标为y，因
为分针每分钟旋转 弧度，所以针尖末端对应的点在角
（弧度）的终边上，从而其纵坐标y关于时间t变化的函数关系为
在物理学和工程技术的许多问题中，经常也会遇到形如
的函数（其中A、ω、φ均是常数）．例如，物
体做简谐运动（如单摆或弹簧的振动）的过程中，物体离开平衡位
置的位移y与时间 的关系为
上式中，A是物体振动时离开平衡位置的最大距离，称为该振动的振幅 ．A越大，振动的幅度越大
单摆或弹簧往复振动一次所需的时间 称为该振动的
周期（即前面所说的最小正周期）．ω越大，振动的周期越小．
在单位时间内振动的次数 称为该振动的频率 而 相应地称为圆频率．ω越大，振动的频率越大
称为该振动的相位 ．当 时的相位φ称为初始相位 ． 下面，我们借助于计算器（机）来探讨 的变化对函数 图像的影响
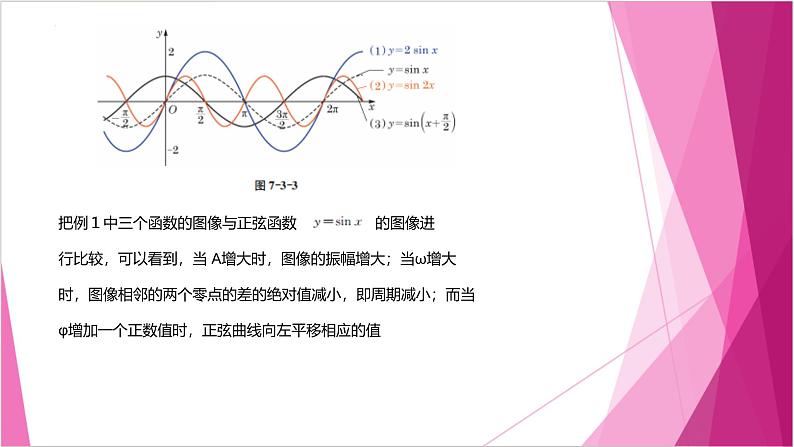
例１ 当函数 中的常数 分别取下列各组值时，用计算器（机）在同一平面直角坐标系中作出它们的图像：
用计算器（机）可作出相应的图像，如图 所示：
把例１中三个函数的图像与正弦函数 的图像进行比较，可以看到，当 A增大时，图像的振幅增大；当ω增大时，图像相邻的两个零点的差的绝对值减小，即周期减小；而当φ增加一个正数值时，正弦曲线向左平移相应的值
我们已经知道函数 的定义域为R，值域为 ，最小正周期为 那么，如何作出函数 的大致图像呢
我们可先用“五点法”作出它在长度为一个周期的区间内的大
致图像，再向左、右不断平移，就可以得到函数
例２ 作出函数 的大致图像，并指出其振幅、频率和初始相位
解 函数 的最小正周期
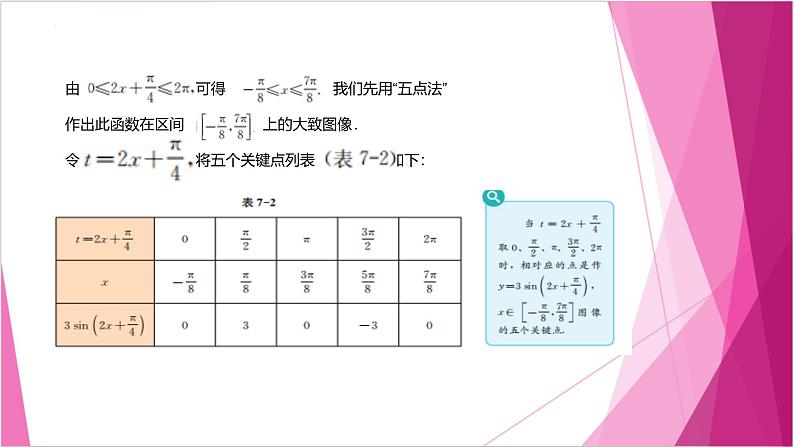
由 可得 我们先用“五点法”作出此函数在区间 上的大致图像．令 将五个关键点列表 如下：
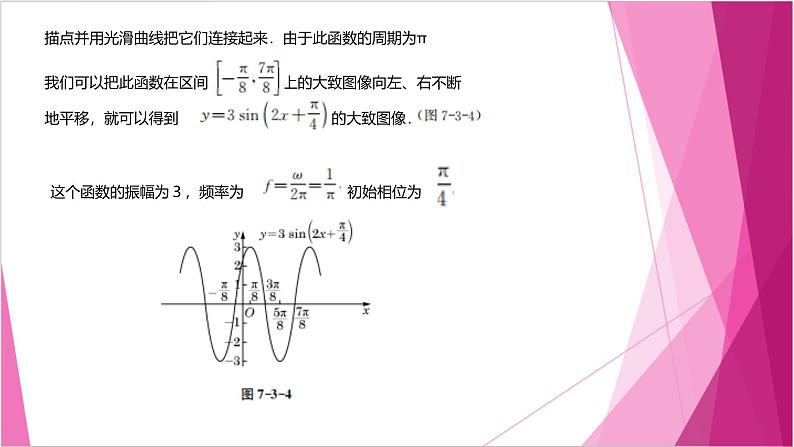
描点并用光滑曲线把它们连接起来．由于此函数的周期为π
我们可以把此函数在区间 上的大致图像向左、右不断地平移，就可以得到 的大致图像．
这个函数的振幅为３，频率为 初始相位为
例３ 已知交流电的电流强度 关于时间t的函数为 ，其中 根据图像求出它的周期、频率和电流的最大值，并写出 的值．
解 由图像可以看出，这个交流电的周期 ，频率
电流的最大值为１０Ａ．
１．作出下列函数的大致图像：
２．下列函数中，与函数 的图像形状相同的是
３．下图是函数 的图像，请根据图中的信息，写出该图像的一个函数 表达式
1、要得到函数y＝sin 的图像，只要将函数y＝sin2x的图像（ ）
2、由y＝3sinx的图象变换得到y＝3sin 的图像主要有两个过程：先平移后伸缩和先伸缩后平移，前者需向左平移________个单位长度，后者需向左平移________个单位长度．
3、已知函数f(x)＝A sin (ωx＋φ)(A＞0，ω＞0，
的一段图像如图所示；（1）求f(x)的解析式；（2）求f(x)的单调减区间，并指出f(x)的最大值及取到最大值时x的集合。
【解析】（1）由图像可以得到函数f(x)的振幅A＝3，