北京市顺义牛栏山第一中学2024-2025学年高一上学期期中考试数学试卷（解析版）-A4

这是一份北京市顺义牛栏山第一中学2024-2025学年高一上学期期中考试数学试卷（解析版）-A4，共14页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
一、单选题（每小题4分，共40分）
1. 若集合，，则（ ）
A. B. C. D.
【答案】A
【解析】
【分析】根据并集运算直接求得结果.
【详解】因为，所以.
故选：A.
2. 如果，那么下列不等式中正确的是（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】特殊值判断A、B、C；由不等式性质判断D.
【详解】若时，，，，即A、B、C错；
由，则恒成立，D对.
故选：D
3. 命题“，”的否定为（ ）
A. ，B. ，
C. ，D. ，
【答案】C
【解析】
【分析】通过修改量词和否定结论，即可得到命题的否定.
【详解】修改量词，否定结论，可得原命题的否定为：.
故选：C.
4. 下列函数中，既是其定义域上的单调函数，又是奇函数的是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】A选项，定义法得到不为奇函数；B选项，不满足在定义域上单调；C选项，为非奇非偶函数；D选项，满足在定义域上为单调函数，又是奇函数，D正确.
【详解】A选项，定义域为R，且，
故不是奇函数，A错误；
B选项，的定义域为，而在上单调递减，
故不在定义域上单调，B错误；
C选项，的定义域为，不关于原点对称，故为非奇非偶函数，C错误；
D选项，的定义域为R，且，
故为奇函数，且当时，，在上单调递增，
当时，，上单调递增，
又，故在定义域上单调递增，为单调函数，D正确.
故选：D
5. 已知，，则是的（ ）
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
【答案】B
【解析】
【分析】根据集合的包含关系判断可得出结论.
【详解】因为，因此，是的必要不充分条件.
故选：B.
6. 已知，，且，则的最小值为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】将代数式与相乘，展开后利用基本不等式可求得的最小值.
【详解】因为，，且，
则，
当且仅当时，即当时，等号成立，故的最小值为.
故选：C.
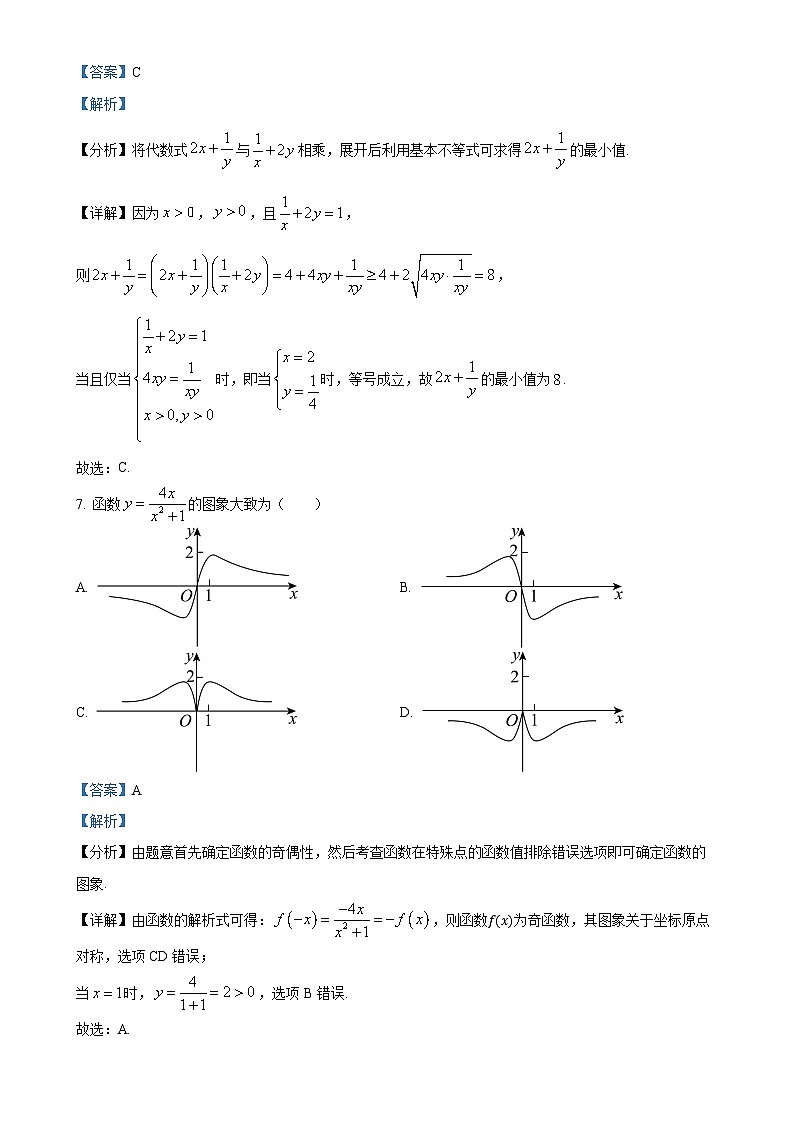
7. 函数的图象大致为（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】由题意首先确定函数的奇偶性，然后考查函数在特殊点的函数值排除错误选项即可确定函数的图象.
【详解】由函数的解析式可得：，则函数f(x)为奇函数，其图象关于坐标原点对称，选项CD错误；
当时，，选项B错误.
故选：A.
【点睛】函数图象的识辨可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置．(2)从函数的单调性，判断图象的变化趋势．(3)从函数的奇偶性，判断图象的对称性．(4)从函数的特征点，排除不合要求的图象．利用上述方法排除、筛选选项．
8. 已知，则下列不等式一定成立的是（ ）.
A. B. C. D.
【答案】D
【解析】
【分析】利用不等式的性质进行推理分析即可.
【详解】由，两边同时除以得：，故A错误；
由，两边同时乘以得：，故B错误；
由，两边同时平方得：，故C错误；
由，两边同时乘以得：，故D正确；
故选：D.
9. 已知函数在定义域上是单调函数，则实数的取值范围为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】根据分段函数和单调性相关知识直接求解.
【详解】因为函数在定义域上单调函数，
显然函数在定义域上单调递减，
则，解得.
故选：B
10. 对于函数，若，则称x为的“不动点”，若，则称x为的“稳定点”，记，，则下列说法错误的是（ ）
A. 对于函数，有成立
B. 若是二次函数，且A是空集，则B为空集
C. 对于函数，有成立
D. 对于函数，存在，使得成立
【答案】D
【解析】
【分析】根据所给定义结合函数的性质一一判断即可；
【详解】解：对于A：函数，，故A正确.
对于B：若A是空集，则恒成立或恒成立.若恒成立，用代替x可得，同理可得，所以无解，即B为空集，故B正确.
对于C：函数，设方程的解为，则，，即，因为函数在R上单调递减，且，所以函数在R上单调递增，且.又因为，所以是方程的唯一解，则，故C正确.
对于D：函数，，，，故D错误.
故选：D
二、填空题（每小题5分，共25分）
11. 函数的定义域为_____________.
【答案】
【解析】
【分析】由函数有意义，列出不等式组求解即得.
【详解】函数有意义，则，解得且，
所以函数的定义域为.
故答案为：
12. 函数的值域为_____.
【答案】
【解析】
【分析】先求解出的值域，然后结合指数函数的单调性可求的值域.
【详解】令，则，
因为在上单调递减，所以，且当时，，
所以的值域为，
故答案为：.
13. 已知，则__________．
【答案】
【解析】
【分析】在等式中，令可得的值.
【详解】在等式中，令，可得.
故答案为：.
14. 函数（且）的图象必过定点的坐标是______.
【答案】
【解析】
【分析】令，计算出对应的，则定点坐标可知.
【详解】令，则，所以，
所以图象所过定点坐标为.
故答案为：.
15. 设函数.给出下列四个结论：
①函数的值域是；
②，有；
③，使得；
④若互不相等的实数满足，则的取值范围是.
其中所有正确结论的序号是_________.
【答案】①③④
【解析】
【分析】对于①，利用二次函数与反比例函数的图像性质画出函数图1，结合图像即可判断；
对于②，举反例排除即可；
对于③，将问题转化为与有交点，作出图2即可判断；
对于④，结合图1对进行分析即可.
【详解】对于①，因为，
所以由二次函数与反比例函数的图像性质可画出函数图象，如图1，
由的图像易知的值域是，故①正确；
对于②，易得，，显然在上并不单调递增，所以②说法不成立，故②错误；
对于③，假设存，，则，即，
即与有交点，作出图像，如图2，显然假设成立，故③正确；
对于④，由图1易知，则，
因为，所以，即，解得，
所以，即的取值范围是，故④正确；
综上：①③④正确.
故答案为：①③④.
三、解答题（共85分）
16. 已知集合，集合，集合.
（1）求；
（2）若，求的取值范围.
【答案】（1）
（2）或
【解析】
【分析】（1）先求解出一元二次不等式的解集为集合，再根据补集运算求解出，最后根据交集运算可求；
（2）先根据条件分析出，然后讨论和两种情况，列出对应不等式组，求解出结果.
【小问1详解】
因为，解得或，
所以或x>5，所以，
因为，所以.
【小问2详解】
因为，所以，
当时，成立，此时，即；
当时，若，则需，解得，
综上所述，的取值范围是或.
17. 某公司计划投资A，B两种金融产品，根据市场调查与预测，A产品的利润与投资金额x的函数关系为，B产品的利润与投资金额x的函数关系为（注：利润与投资金额单位：万元）．现在该公司有100万元资金，并全部投入A，B两种产品中且均有投，其中x万元资金投入A产品．
（1）请把A，B两种产品利润总和y表示为x的函数，并直接写出定义域；
（2）在（1）的条件下，当x取何值时才能使公司获得最大利润？
【答案】（1）
（2）时，利润最大.
【解析】
【分析】（1）A，B对于投资金额下的利润求和得到总利润的函数关系式即可；
（2）结合函数式特点利用均值不等式求函数最值.
【小问1详解】
由题意，万元投入A产品，则万元投入B产品，则
，.
【小问2详解】
由（1）得，
，
当且仅当，即时等号成立，
所以当时，公司利润最大.
18. 已知函数是定义在R上的奇函数，且当时，.
（1）已知函数的部分图象如图所示，
请根据条件将图象补充完整，并写出函数的解析式和单调递减区间；
（2）若关于的方程有个不相等的实数根，求实数的取值范围．（只需写出结论）
（3）写出解不等式的解集．
【答案】（1）答案见解析
（2）
（3）
【解析】
【分析】（1）利用奇函数的性质，即可画出函数的图象，再根据图象求函数的单调递增区间；利用函数是奇函数，求函数的解析式；
（2）利用数形结合，转化为y=fx与的图象有个交点，从而得解；
（3）分，两种情况，数形结合可得出原不等式的解集.
【小问1详解】
解：因为是定义在R上的奇函数，其图象关于原点对称，则补充图象如图，

结合图象可知，函数的单调递减区间为和1,+∞．
因为当时，，
所以当时， ，所以，
因为是定义在R上的奇函数，所以，
所以当 时，，
故的解析式为.
【小问2详解】
解：因为有个不相等的实数根，等价于y=fx与的图象有个交点，
结合（1）中y=fx的图象可知，当时，y=fx与的图象有个交点，
所以.
【小问3详解】
解：当时，可得，结合图象可得；
当时，可得，结合图象可得.
综上所述，不等式的解集为.
19. 已知
（1）若当时，恒成立，求实数的取值范围；
（2）求关于的不等式的解集.
【答案】（1）
（2）答案见解析
【解析】
【分析】（1）将问题转化为“x∈2,4时，”，利用基本不等式求解出最小值，由此可求的范围；
（2）先化简不等式，然后根据与的关系进行分类讨论，由此求解出不等式的解集.
【小问1详解】
因为x∈2,4时，恒成立，所以x∈2,4时，恒成立，
所以x∈2,4时，即可，
因为，当且仅当时取等号，
所以，所以，
所以的取值范围是.
【小问2详解】
，
当，即时，此时不等式为和，解集为；
当或时，此时，的解集为；
当或时，此时，的解集为；
综上所述，时，解集为；
时，解集为；
时，解集.
20. 已知函数是定义域为的奇函数.
（1）求函数的解析式；
（2）用定义证明在定义域上是增函数；
（3）求不等式的解集.
【答案】（1）；
（2）证明见解析； （3）．
【解析】
【分析】（1）由奇偶性的函数的定义域关于0对称求得，由奇函数的性质求得得解析式；
（2）根据单调性的定义证明；
（3）由单调性的性质及定义域列不等式组求解．
【小问1详解】
由题意，，，又，
满足题意．
所以；
小问2详解】
设任意的且，，
又，所以，所以，，
所以在定义域上是增函数；
【小问3详解】
由（2）得，解得．解集为．
21. 已知集合
（1）分别判断、、是否属于集合；
（2）写出所有满足集合的不超过的正偶数；
（3）已知集合，证明：“”是“”的充分不必要条件.
【答案】（1）、、都属于集合，理由见解析
（2）、、
（3）证明见解析
【解析】
【分析】（1）根据集合中元素的特征判断即可；
（2）由集合的描述：，讨论、同奇或同偶、一奇一偶，即可确定的奇偶性，进而写出所有满足集合的不超过的正偶数；
（3）由，即可得到充分性成立，再利用特殊值判断必要性不成立.
【小问1详解】
解：因为，，，所以，、、都属于集合.
【小问2详解】
解：集合，，
①若、同奇或同偶时，、均为偶数，为的倍数；
②当、一奇一偶时，、均为奇数，为奇数，
综上，所有满足集合的偶数为．
因此，满足集合的不超过的正偶数有、、.
【小问3详解】
证明：集合，则恒有，
所以，，即一切奇数都属于，
又，而，
所以，“”是“”的充分不必要条件.