

所属成套资源:全国通用 中考数学 二次函数压轴题专题练习
全国通用 中考数学 二次函数压轴题专题练习 11等腰三角形存在性问题 (含答案解析版)
展开
这是一份全国通用 中考数学 二次函数压轴题专题练习 11等腰三角形存在性问题 (含答案解析版),共24页。
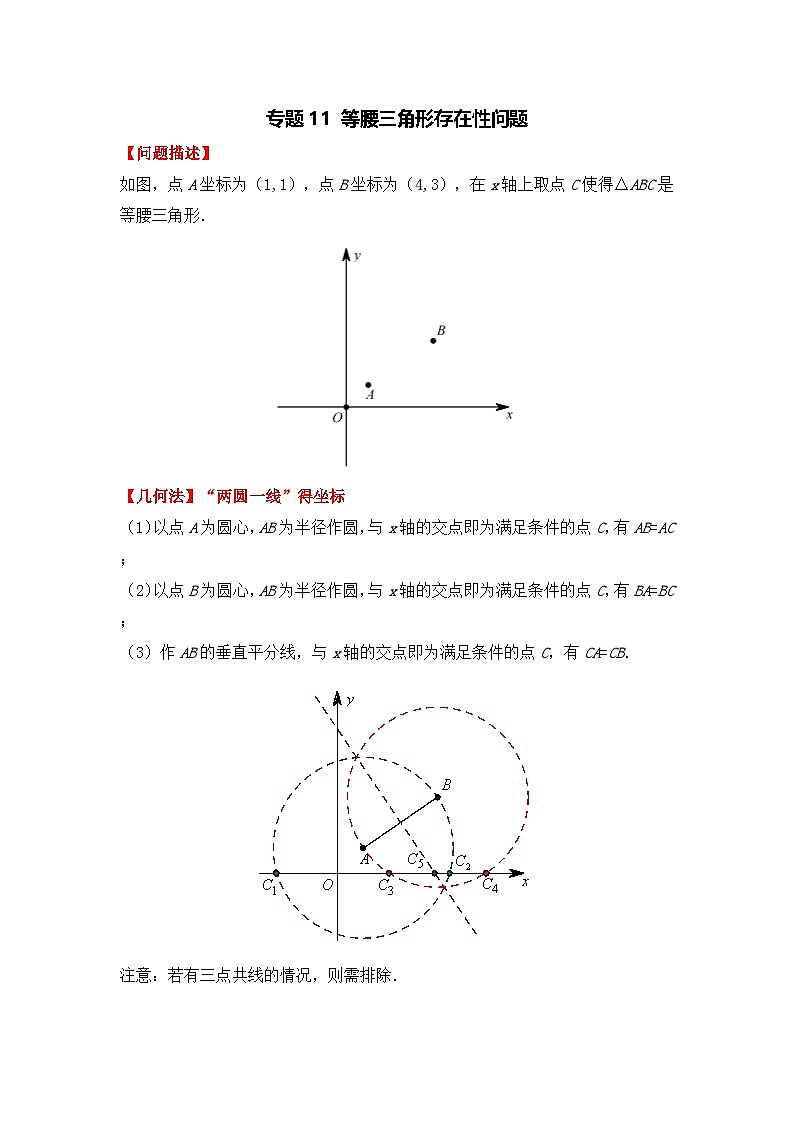
如图,点A坐标为(1,1),点B坐标为(4,3),在x轴上取点C使得△ABC是等腰三角形.
【几何法】“两圆一线”得坐标
(1)以点A为圆心,AB为半径作圆,与x轴的交点即为满足条件的点C,有AB=AC;
(2)以点B为圆心,AB为半径作圆,与x轴的交点即为满足条件的点C,有BA=BC;
(3)作AB的垂直平分线,与x轴的交点即为满足条件的点C,有CA=CB.
注意:若有三点共线的情况,则需排除.
【代数法】表示线段构相等
(1)表示点:设点坐标为(m,0),又A点坐标(1,1)、B点坐标(4,3),
(2)表示线段:,
(3)分类讨论,列出方程:根据,可得:,
(4)求解得答案:解得:,故坐标为.
【小结】
几何法:(1)“两圆一线”作出点;
(2)利用勾股、相似、三角函数等求线段长,由线段长得点坐标.
代数法:(1)表示出三个点坐标A、B、C;
(2)由点坐标表示出三条线段:AB、AC、BC;
(3)根据题意要求取①AB=AC、②AB=BC、③AC=BC;
(4)列出方程求解.
1.(2024秋•红塔区期中)综合与探究
如图,二次函数y=﹣x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C,点A的坐标为(﹣4,0),且OA=OC,E是线段OA上的一个动点,过点E作直线EF垂直于x轴交直线AC和抛物线分别于点D、F.
(1)求抛物线的解析式;
(2)设点E的横坐标为m,当m为何值时,线段DF有最大值,并写出最大值为多少;
(3)点P是直线AC上的一个动点,若使三角形PBC是等腰三角形,求出点P的坐标.
【解答】解:(1)二次函数y=﹣x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C,A(﹣4,0),且OA=OC,
∴OA=4,
∴OC=4,
∴点C的坐标为C(0,4),
把点A,点C的坐标代入二次函数解析式y=﹣x2+bx+c得:
,
解得,,
∴二次函数解析式为y=﹣x2﹣3x+4;
(2)当m=﹣2时,DF有最大值,且最大值为4;理由如下:
由(1)可知,二次函数解析式为y=﹣x2﹣3x+4,且A(﹣4,0),C(0,4),
∴设直线AC所在直线的解析式为y=kx+b(k≠0),将点A,点C的坐标代入得:
,
解得,,
∴直线AC的解析式为y=x+4,
∵点E的横坐标为m,直线EF垂直于x轴交直线AC和抛物线分别于点D、F,
∴点D、F的横坐标为m,
∴D(m,m+4),F(m,﹣m2﹣3m+4),
∴DF=﹣m2﹣3m+4﹣(m+4)=﹣m2﹣4m=﹣(m+2)2+4,
∴当m=﹣2时,DF有最大值,且最大值为4;
(3)∵二次函数y=﹣x2﹣3x+4的图象与x轴交于A,B两点,且A(﹣4,0),
∴令y=0时,x2+3x﹣4=0,则x1=﹣4,x2=1,
∴B(1,0),且C(0,4),
在Rt△BOC,OB=1,OC=4,,
点P是直线AC上的一个动点,若使三角形PBC是等腰三角形,设P(n,n+4),分三种情况:
当CP=CB时,即CP2=CB2,
∴,
解得,
∴点P的坐标为或;
当BP=BC时,即BP2=CB2,
∴,
解得n=0(舍去),n=﹣3,
∴P(﹣3,1),
当PC=PB时,即PC2=PB2,
∴(n﹣1)2+(n+4)2=n2+(n+4﹣4)2,
解得,
∴点P的坐标为,
综上,若使三角形PBC是等腰三角形,点P的坐标为或或(﹣3,1)或.
2.(2024秋•武威月考)如图,点C为二次函数y=(x+1)2的顶点,直线y=﹣x+m与该二次函数图象交于A(﹣3,4)、B两点(点B在y轴上),与二次函数图象的对称轴交于点D.
(1)求m的值及点C坐标;
(2)在该二次函数的对称轴上是否存在点Q,使得以A,C,Q为顶点的三角形是等腰三角形?若存在,请求出符合条件的Q点的坐标;若不存在,请说明理由.
【解答】解:(1)点C为二次函数y=(x+1)2的顶点,直线y=﹣x+m与该二次函数图象交于A(﹣3,4)、B两点(点B在y轴上),
∴4=3+m,
∴m=1,
∴y=﹣x+1,
∴B(0,1),
二次函数解析式为y=(x+1)2,
顶点坐标为C(﹣1,0);
(2)在该二次函数的对称轴上存在点Q,使得以A,C,Q为顶点的三角形是等腰三角形;理由如下:
∵顶点坐标为C(﹣1,0),
∴对称轴为直线x=﹣1,
过点A作AE⊥CD于点E,
在Rt△ACE中,.
①当AQ=CQ时,设CQ=m,
在Rt△AQE中,AE2+EQ2=AQ2,
∴22+(4﹣m)2=m2,
解之得,
∴;
②当AC=AQ时,根据等腰三角形三线合一得:CE=QE=4,
∴CQ=2CE=8,
∴Q2(﹣1,8);
③当CA=CQ时,,
∴,.
综上所述:点Q的坐标为或(﹣1,8)或或.
3.(2024秋•宝坻区校级月考)已知:如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式;
(2)过P点作y轴的平行线交直线BC于点E,求线段PE的最大值.
(3)在直线BC找一点Q,使得△QOC为等腰三角形,直接写出Q点.
【解答】解:(1)∵二次函数y=x2+bx+c的图象经过点B(3,0),点C(0,﹣3),
∴,
∴.
∴这个二次函数的表达式为y=x2﹣2x﹣3.
(2)∵点P是直线BC下方的抛物线上一动点,
∴设P(m,m2﹣2m﹣3),0<m<3,
设直线BC的解析式为y=kx+a,
∴,
∴,
∴直线BC的解析式为y=x﹣3.
∵过P点作y轴的平行线交直线BC于点E,
∴E(m,m﹣3),
∴PE=m﹣3﹣(m2﹣2m﹣3)=﹣m2+3m=﹣+,
∵﹣1<0,
∴当m=时,PE有最大值为.
∴线段PE的最大值为.
(3)①∵C(0,﹣3),
∴OC=3,
∴OB=OC=3,
∴当点Q与点B重合时,满足△QOC为等腰三角形,
∴Q(3,0);
②当QO=QC时,过点Q作QD⊥OC于点D,如图,
∵QO=QC,QD⊥OC,
∴OD=OC=,
∴点Q的纵坐标为﹣,
∵点Q在直线y=x﹣3上,
∴﹣=x=3,
∴x=.
∴Q(,﹣);
③当QC=OC=3时,过点Q作QE⊥OB于点E,如图,
∵OB=OC=3,
∴BC=3,∠OCB=∠OBC=45°.
∴BQ=BC=CQ=3﹣3,
∴EQ=BE=BQ=3﹣,
∴OE=OB﹣BE=,
∴Q(,3);
当QC=OC=3时,过点Q作QF⊥OC于点F,如图,
∵OB=OC=3,
∴∠OCB=∠OBC=45°.
∴∠QCF=45°,
∵QF⊥OC,
∴QF=CF=CQ=,
∴OF=OC+CF=3+,
∴Q(﹣,﹣3﹣).
综上,在直线BC找一点Q,使得△QOC为等腰三角形,Q点坐标为(3,0)或(,﹣)或(,3)或(﹣,﹣3﹣).
4.(2024•雅安)在平面直角坐标系中,二次函数y=ax2+bx+3的图象与x轴交于A(1,0),B(3,0)两点,与y轴交于点C.
(1)求二次函数的表达式;
(2)如图①,若点P是线段BC上的一个动点(不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,当线段PQ的长度最大时,求点Q的坐标;
(3)如图②,在(2)的条件下,过点Q的直线与抛物线交于点D,且∠CQD=2∠OCQ.在y轴上是否存在点E,使得△BDE为等腰三角形?若存在,直接写出点E的坐标;若不存在,请说明理由.
【解答】解:(1)由题意得:y=a(x﹣1)(x﹣3)=a(x2﹣4x+3)=ax2+bx+3,
则a=1,
则抛物线的表达式为:y=x2﹣4x+3;
(2)由抛物线的表达式知,点C(0,3),
由点B、C的坐标得,直线CB的表达式为:y=﹣x+3,
设点Q(x,x2﹣4x+3),则点P(x,﹣x+3),
则PQ=﹣x+3﹣(x2﹣4x+3)=﹣x2+3x,
∵﹣1<0,
故PQ有最大值,
此时x=,则y=x2﹣4x+3=﹣,
即点Q(,﹣);
(3)存在,理由:
由点C、Q的坐标得,直线CQ的表达式为:y=﹣x+3,
过点Q作TQ∥y轴交x轴于点T,则∠TQA=∠QCO,
∵∠CQD=2∠OCQ,∠TQA=∠QCO,
则∠CQT=∠QQT,
即直线AQ和DQ关于直线QT对称,
则直线DQ的表达式为:y=(x﹣)﹣,
联立上式和抛物线的表达式得:x2﹣4x+3=(x﹣)﹣,
解得:x=(舍去)或5,
即点D(5,8);
设点E(0,y),由B、D、E的坐标得,BD2=68,DE2=25+(y﹣8)2,BE2=9+y2,
当DE=BD时,
则68=25+(y﹣8)2,
解得:y=8±,即点E(0,8±);
当DE=BE或BD=BE时,
同理可得:25+(y﹣8)2=9+y2或9+y2=68,
解得:y=5或±,
即点E(0,5)或(0,±);
综上,点E(0,8±)或(0,5)或(0,±).
5.(2024•仁布县一模)如图,二次函数y=x2+bx+c的图象与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,D为抛物线的顶点.
(1)求抛物线的解析式;
(2)求△DBC的面积;
(3)在抛物线对称轴上,是否存在一点P,使P,B,C为顶点的三角形为等腰三角形?若存在,写出点P的坐标;若不存在,请说明理由.
【解答】解:(1)∵抛物线 y=x2+bx+c 经过 A(﹣1,0)、B(3,0)两点,
∴,
解得,
∴抛物线的函数关系式是y=x2﹣2x﹣3.
(2)如图,过D作x轴的垂线,交BC于E,垂足为F,
由y=x2﹣2x﹣3可得顶点D(1,﹣4),C(0,﹣3),
∴直线BC的解析式为y=x﹣3,
∴E(1,﹣2),
∴DE=(﹣2)﹣(﹣4)=2,
∴.
(3)存在.P1(1,﹣1),P2(1,,,,.
设点P(1,a),连接PB,PC,
由P,B两点的水平距离为|1﹣3|,竖直距离为|a﹣0|,得PB2=(1﹣3)2+a2=4+a2,
同理可得PC2=1+(a+3)2=a2+6a+10,BC2=32+32=18,
分类讨论:①若PC=PB,则PC2=PB2,
即a2+6a+10=4+a2,
解得a=﹣1,
即P1(1,﹣1);
②若PC=BC,则PC2=BC2,
即a2+6a+10=18,
解得,,
即,P3(1,;
③若PB=BC,则PB2=BC2,
即4+a2=18,
解得,,
即P4,.
综上,符合条件的P点坐标为P1(1,﹣1),P2(1,,,,.
6.(2024•清镇市校级模拟)人生有低谷,那可是触地反弹前的转折点!如图,关于x的二次函数y=x2+bx+c的图象与x轴相交于A(1,0)和点B,与y轴相交于C(0,3).
(1)求二次函数的表达式.
(2)求线段BC的长.
(3)在y轴上是否存在一点P,使得△PBC为等腰三角形?如不存在,请说明理由;若存在,请直接写出P的坐标.
【解答】解:(1)由题意得:,
解得:,
∴二次函数的表达式为:y=x2﹣4x+3;
(2)令抛物线y=0,则x2﹣4x+3=0,
解得x=1或x=3,
根据题意:B(3,0),
∵C(0,3),
∴BC==3;
(3)存在.
理由:∵BC=3,
点P在y轴上,当△PBC为等腰三角形时分三种情况进行讨论:如图,
①当CP=CB时,PC=3,
又∵C(0,3),
∴点P(0,3±3);
②当BP=BC时,OP=OC=3,
∴P3(0,﹣3);
③当PB=PC时,
∵OC=OB=3,
∴此时P与O重合,
∴P4(0,0);
综上所述,点P的坐标为:(0,3+3)或(0﹣3﹣3)或(0,﹣3)或(0,0).
7.(2024•滨湖区校级二模)二次函数y=ax2+bx﹣4的图象与x轴相交于点A(﹣4,0)和点B(2,0),与y轴相交于点C,顶点为点D.
(1)求该二次函数的表达式;
(2)若抛物线的对称轴l交x轴于点E,点P是线段DE上的一个动点(不与点E重合),连接PC,作PQ⊥PC交x轴于点Q(k,0),求k的取值范围;
(3)连接AD、BD,点M、N分别在线段AB、AD上(均含端点),且∠DMN=∠DBA,若△DMN是等腰三角形,求点M的坐标.
【解答】解:(1)由题意得:y=a(x+4)(x﹣2)=ax2+bx﹣4,
解得:a=,
则抛物线的表达式为:y=x2+x﹣4;
(2)由抛物线的表达式知,点C的坐标为(0,﹣4),定点坐标为:(﹣1,﹣),
由点P在线段DE上,设点P的坐标为(﹣1,a),
则﹣≤a<0,
∵Q(k,0),C(0,﹣4),
∴PQ2=(k+1)2+a2,CP2=1+(a+4)2,CQ2=k2+6,
∵PQ⊥PC,
∴∠QPC=90°,
在Rt△QPC中,CQ2=PQ2+CP2,
∴k2+16=(k+1)2+a2+1+(a+4)2,
整理得k=﹣(a+2)2+3,
∵﹣≤a<0,
∴当a=﹣2时,k取得最大值3;当a=﹣时,k取得最小值﹣,
∴﹣≤k≤3;
(3)由抛物线对称性可得,∠DBA=∠DAB,
∵∠DMN=∠DBA,
∴∠DMN=∠DBA=∠DAB,
把y=0代入y=x2+x﹣4;
解得x1=﹣4,x2=2,
∴点B的坐标为(2,0),
设点M的坐标为(m,0),
∵点M在线段AB上(含端点),
∴﹣4≤m≤2,
①若DN=DM,则∠DMN=∠DNM,
∵∠DMN=∠DAB,
∴∠DAB=∠DNM,
得点N与点A重合,则点M与点B重合,
∴点M的坐标为(2,0);
②若DN=MN,则∠DMN=∠NDM,
∵∠DMN=∠DAB,
∴∠NDM=∠DAB,
∴AM=DM,即m+4=,
解得:m=,
∴点M的坐标为(,0);
③若MN=MD,则∠MND=∠MDN,
∵∠AMD是△BDM的外角,
∴∠AMN+∠DMN=∠BDM+∠DBA,
∵∠DMN=∠DBA,
∴∠AMN=∠BDM,
∵MN=MD,∠MAN=∠DBM,
∴△AMN≌△BDM(AAS),
∴AM=BD,
∴m+4=,
解得:m=,
∴点M的坐标为(,0);
综上所述,若△DMN是等腰三角形,则点M的坐标为(2,0)或(,0)或(,0).
8.(2024•城关区校级一模)如图,关于x的二次函数y=x2+bx+c的图象与x轴相交于点A(1,0)和点B,与y轴相交于点C(0,3).
(1)求二次函数的表达式.
(2)求线段BC的长.
(3)在y轴上是否存在一点P,使△PBC为等腰三角形?直接写出点P的坐标.
【解答】解:(1)把A(1,0)和C(0,3)代入y=x2+bx+c,
,
解得:b=﹣4,c=3,
∴二次函数的表达式为:y=x2﹣4x+3;
(2)令抛物线y=0,则x2﹣4x+3=0,
解得x=1或x=3,
根据题意:B(3,0),
∵C(0,3),
∴;
(3)存在.
理由:∵,
点P在y轴上,当△PBC为等腰三角形时分三种情况进行讨论:如图,
①当CP=CB时,,
又∵C(0,3),
∴,;
②当BP=BC时,OP=OC=3,
∴P3(0,﹣3);
③当PB=PC时,
∵OC=OB=3,
∴此时P与O重合,
∴P4(0,0);
综上所述,点P的坐标为:或或(0,﹣3)或(0,0).
9.(2024春•渠县校级月考)如图,一次函数与x轴、y轴分别交于A、C两点,二次函数y=ax2+bx+c的图象经过A、C两点,与x轴交于另一点B,其对称轴为直线
(1)求该二次函数表达式;
(2)在对称轴上是否存在点P,使△PAC为等腰三角形,若存在,求出点P的坐标;若不存在,请说明理由.
【解答】解:(1)对于,当x=0时,y=﹣2,即点C(0,﹣2),
令,则x=﹣4,即点A(﹣4,0).
∵抛物线的对称轴为直线,则点B(1,0),
∴抛物线与x轴的另一个交点为(﹣4,0),
设二次函数表达式为:y=a(x﹣1)(x+4)=a(x2+3x﹣4),
∵抛物线过点C(0,﹣2),
则﹣4a=﹣2,
解得:,
故抛物线的表达式为:;
(2)存在,
理由:根据题意对称轴,设点,
由点A、C、P的坐标得:,AC2=20,,
当PA=AC时,则,
解得:,
即点P的坐标为:或;
当PA=PC时,则,
解得:t=0,
即点;
当AC=PC时,则,
解得:,
即点P的坐标为:或.
综上,点P的坐标为:或或或或.
10.(2024•兴庆区校级二模)如图,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图象与x轴交于A,B点,与y轴交于点C(0,3),点B的坐标为(3,0),点P是抛物线上一个动点,且在直线BC的上方.
(1)求这个二次函数的解析式;
(2)当点P运动到什么位置时,△BPC的面积最大?请求出点P的坐标和△BPC面积的最大值.
(3)除原点外,在x轴上是否存在一点Q,使得△BCQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
【解答】解:(1)将B(3,0),C(0,3)代入y=﹣x2+bx+c,得:
,解得:,
∴二次函数的解析式为y=﹣x2+2x+3;
(2)如图,过点P作y轴的平行线与BC交于点Q,
设P(x,﹣x2+2x+3),
由点B、C的坐标得,BC的解析式为y=﹣x+3,
则Q(x,﹣x+3),
∴S△CPB=S△BPQ+S△CPQ=PQ×OB=(﹣x2+2x+3+x﹣3)×3=﹣(x﹣)2+≤,
当x=时,△CPB的面积最大,
此时,点P的坐标为(,),△CPB的面积的最大值为;
(3)存在,理由:
设点Q(x,0),
由点B、C、Q的坐标得,BQ2=(x﹣3)2,BC2=18,CQ2=x2+9,
当BQ=CB时,
则(x﹣3)2=18,
解得:x=3±3,
即点Q(3±3,0);
当BQ=CQ或BC=CQ时,
则18=x2+9或(x﹣3)2=9,
解得:x=﹣3(不合题意的值已舍去),
即点Q(﹣3,0),
综上,(3±3,0)或(﹣3,0).
11.(2024•梅州模拟)如图所示,已知二次函数y=ax2+bx+c的图象经过点A(5,0),B(﹣1,0),C(0,﹣5).
(1)求二次函数y=ax2+bx+c的解析式;
(2)直线x=t(0<t<5)交二次函数y=ax2+bx+c的图象于点P,交直线AC于点Q,是否存在实数t,使△CPQ为等腰三角形,若存在,请求出这样的t值;若不存在,请说明理由.
【解答】解:(1)由题意得,抛物线的表达式为:y=a(x﹣5)(x+1)=a(x2﹣4x﹣5),
则﹣5a=﹣5,
解得:a=1,
则抛物线的表达式为:y=x2﹣4x﹣5;
(2)存在,理由:
由点A、C的坐标得,直线AC的表达式为:y=x﹣5,
则点P(t,t2﹣4t﹣5)、点Q(t,t﹣5),
由点P、Q、C的坐标得,PQ2=(﹣t2+5t)2,PC2=t2+(t2﹣4t)2,CQ2=2t2,
当PQ=CQ时,
则(﹣t2+5t)2=2t2,
解得:t=0(舍去)或3或4;
当PQ=PC或PC=CQ时,
则(﹣t2+5t)2=t2+(t2﹣4t)2或t2+(t2﹣4t)2=2t2,
解得:t=5﹣或3,
综上,t=5﹣或3或4.
12.(2024春•锡山区期中)如图1,二次函数y=ax2+2ax+3的图象与x轴交于点A、B,与y轴交于点C,且OA=OC.点P为抛物线第二象限上一动点.
(1)直接写出该二次函数的表达式为 y=﹣x2﹣2x+3 ;
(2)连接PA、PC、BC,求四边形ABCP面积的最大值;
(3)如图2,连结BP交AC于点H,过点P作y轴的平行线交AC于点Q.当△PQH为等腰三角形时,求出点P的坐标.
【解答】解:(1)OA=OC=3,
则点A(﹣3,0),
将点A的坐标代入抛物线表达式得:0=9a﹣6a+3,
解得:a=﹣1,
则抛物线的表达式为:y=﹣x2﹣2x+3,
故答案为:y=﹣x2﹣2x+3;
(2)如图2,
由点A、C的坐标得,直线AC的表达式为:y=x+3,
设点P(m,﹣m2﹣2m+3),则点Q(m,m+3),
则PQ=﹣m2﹣2m+3﹣m﹣3=﹣m2﹣3m,
则四边形ABCP面积=S△ABC+S△ACP=AB×CO+PQ×AO=4×3+(﹣m2﹣3m)×3=(﹣m2﹣3m)+6,
∵<0,
故四边形ABCP面积存在最大值,
当m=﹣时,四边形ABCP面积的最大值为;
(3)设点P(m,﹣m2﹣2m+3),则点Q(m,m+3),
由点B、P的坐标得,直线BP的表达式为:y=﹣(m+3)(x﹣1),
联立上式和直线AC的表达式得:﹣(m+3)(x﹣1)=x+3,
解得:xH=,则点H的坐标为:(,+3),
由直线AC的表达式知,其和x轴正半轴的夹角为45°,
如果PH=PQ,则∠PHQ=45°,则∠QPH=90°,故PH=PQ不存在,
则QH=(xH﹣xQ)=(﹣m),
而PQ=﹣m2﹣3m,
当PH=QH时,
则点H在PQ的中垂线上,则yH=(yP+yQ),
∴+3=(﹣m2﹣2m+3+m+3),
解得:m=﹣3(舍去)或﹣2,
即点P(﹣2,3);
当PQ=QH时,即(﹣m)=﹣m2﹣3m,
解得:m=﹣3(舍去)或﹣4,
即点P(,6﹣7),
综上,点P的坐标为:(﹣2,3)或(,6﹣7).
相关试卷
这是一份全国通用 中考数学 二次函数压轴题专题练习 11等腰三角形存在性问题(不含答案版),共14页。
这是一份全国通用 中考数学 二次函数压轴题专题练习 10正方形存在性问题(含答案解析版),共22页。试卷主要包含了【实践探究】,综合与探究等内容,欢迎下载使用。
这是一份全国通用 中考数学 二次函数压轴题专题练习 10正方形存在性问题(不含答案版),共7页。试卷主要包含了【实践探究】,综合与探究等内容,欢迎下载使用。










