广东省深圳市宝安区观澜二中2024-2025学年七年级上学期期中数学试卷

这是一份广东省深圳市宝安区观澜二中2024-2025学年七年级上学期期中数学试卷，共19页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。
1．（3分）下列几何体中，属于棱柱的是（ ）
A．B．C．D．
2．（3分）把卫星看成点，则卫星在预定轨道飞行留下的痕迹体现了（ ）
A．点动成线B．线动成面
C．面动成体D．面面相交成线
3．（3分）2024的相反数等于（ ）
A．﹣2024B．2024C．D．
4．（3分）下列四个数中，绝对值最大的是（ ）
A．2B．C．0D．﹣3
5．（3分）如果|a+2|+|b﹣1|＝0，那么（a+b）2023的值为（ ）
A．﹣2023B．2023C．﹣1D．1
6．（3分）若代数2x2+3x的值为5，则代数式4x2+6x﹣9的值是（ ）
A．1B．﹣1C．4D．﹣4
7．（3分）我们规定一种新运算“★”，其含义：对于有理数a，b，a★b＝a2﹣ab﹣b，则计算（﹣3）★（﹣1）的结果是（ ）
A．﹣11B．5C．7D．13
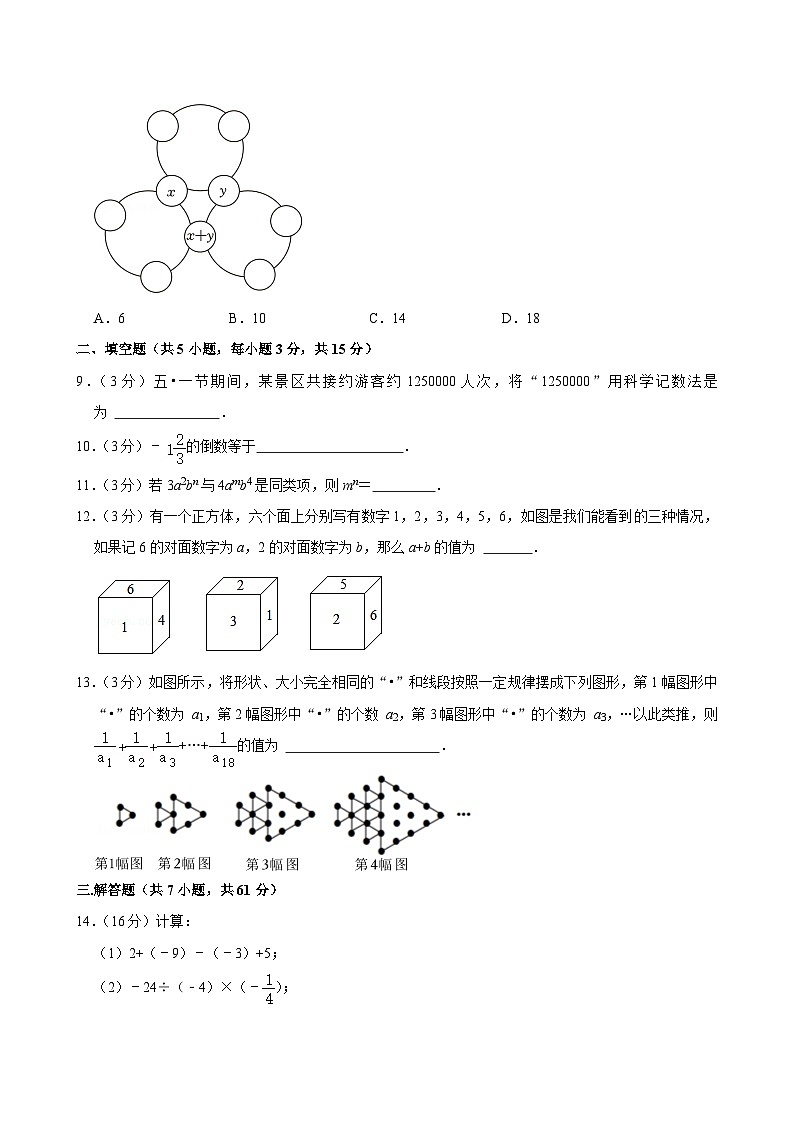
8．（3分）“幻方”最早记载于春秋时期的《大戴礼记》中，现将数字1～9填入如图所示的“幻方”中，使得每个圆圈上的四个数字的和都等于21，若每个圆圈上的四个数字的平方和分别记A、B、C，且A+B+C＝411．如果将交点处的三个圆圈填入的数字分别记作为x、y、x+y，则xy的值为（ ）
A．6B．10C．14D．18
二、填空题（共5小题，每小题3分，共15分）
9．（3分）五•一节期间，某景区共接约游客约1250000人次，将“1250000”用科学记数法是为 ．
10．（3分）﹣的倒数等于 ．
11．（3分）若3a2bn与4amb4是同类项，则mn＝ ．
12．（3分）有一个正方体，六个面上分别写有数字1，2，3，4，5，6，如图是我们能看到的三种情况，如果记6的对面数字为a，2的对面数字为b，那么a+b的值为 ．
13．（3分）如图所示，将形状、大小完全相同的“•”和线段按照一定规律摆成下列图形，第1幅图形中“•”的个数为 a1，第2幅图形中“•”的个数 a2，第3幅图形中“•”的个数为 a3，…以此类推，则+…+的值为 ．
三.解答题（共7小题，共61分）
14．（16分）计算：
（1）2+（﹣9）﹣（﹣3）+5；
（2）﹣24÷（﹣4）×（﹣）；
（3）；
（4）﹣32﹣（5﹣7）×6+（﹣2）3÷8．
15．（6分）化简求值：2（3a2b﹣ab2）﹣3（2a2b﹣ab2+ab），其中a＝，b＝﹣2．
16．（8分）如图是由棱长都为1cm的6块小正方体组成的简单几何体．
（1）请在方格中画出该几何体的三个视图．
（2）如果在这个几何体上再添加一些小正方体，并保持主视图和左视图不变，最多可以再添加 块小正方体，
17．（7分）元旦放假时，小明一家三口一起乘小轿车去乡下探望爷爷、奶奶和外公、外婆．早上从家里出发，向东走了6千米到超市买东西，然后又向东走了1.5千米到爷爷家，中午从爷爷家出发向西走了12千米到外公家，晚上返回家里．
（1）若以家为原点，向东为正方向，用1个单位长度表示1千米，请将超市、爷爷家和外公家的位置在下面数轴上分别用点A、B、C表示出来；
（2）问超市A和外公家C相距多少千米？
（3）若小轿车每千米耗油0.08升，求小明一家从出发到返回家所经历路程小车的耗油量．（精确到0.1升）
18．（6分）如图是一个“数值转换机”（箭头是指数进入转换机的路径，方框是对进入的数进行转换的转换机）．
（1）当小明输入4，7这两个数时，则两次输出的结果依次为 ， ；
（2）你认为当输入数等于 时（写出一个即可），其输出结果为0；
（3）你认为这个“数值转换机”不可能输出 数；
（4）有一次，小明操作的时候，输出的结果是2，聪明的你判断一下，小明输入的正整数是 （用含自然数n的代数式表示）．
19．（9分）我国南宋时期杰出的数学家杨辉是钱塘人，如图所示的图表是他在《详解九章算法》中记载的“杨辉三角”．
此图揭示了（a+b）n（n为非负整数）的展开式的项数及各项系数的有关规律，由此规律可解决如下问题：
（1）请在图中括号内的数为 ；
（2）（a+b）20展开式共有 项，第19项系数为 ；
（3）根据上面的规律，写出（a+b）6的展开式： ；
（4）利用上面的规律计算：35﹣5×34+10×33﹣10×32+5×3﹣1；
（5）假如今天是星期五，那么再过621天是星期几？（写过程）
20．（9分）将一条数轴在原点O和点B处各折一下，得到如图所示的“折线数轴”，图中点A表示﹣10，点B表示10，点C表示18．我们称点A和点C在数轴上的“友好距离”为28个单位长度．动点P从点A出发，以2单位长度/秒的速度沿着“折线数轴”向其正方向运动．当运动到点O与点B之间时速度变为原来的一半．经过点B后立刻恢复原速；同时，动点Q从点C出发，以1单位长度/秒的速度沿着“折线数轴”向其负方向运动，当运动到点B与点O之间时速度变为原来的两倍，经过O后也立刻恢复原速．设运动的时间为t秒．
（1）动点P从点A运动至点C需要 秒，动点Q从点C运动至点A需要 秒；
（2）P，Q两点相遇时，求出相遇点M在“折线数轴”上所对应的数；
（3）是否存在t值，使得点P和点Q在“折线数轴”上的“友好距离”等于点A和点B在“折线数轴”上的“友好距离”？若存在，求出t的值；若不存在，请说明理由．
2024-2025学年广东省深圳市宝安区观澜二中七年级（上）期中数学试卷
参考答案与试题解析
一、选择题（共8小题，每小题3分，共24分）
1．（3分）下列几何体中，属于棱柱的是（ ）
A．B．C．D．
【答案】D
【分析】有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的多面体叫做棱柱，由此可选出答案．
【解答】解：A、圆锥属于锥体，故此选项不合题意；
B、圆柱属于柱体，故此选项不合题意；
C、棱锥属于锥体，故此选项不合题意；
D、长方体属于棱柱，故此选项符合题意；
故选：D．
【点评】本题考查棱柱的定义，属于基础题，掌握基本的概念是关键．
2．（3分）把卫星看成点，则卫星在预定轨道飞行留下的痕迹体现了（ ）
A．点动成线B．线动成面
C．面动成体D．面面相交成线
【答案】A
【分析】把卫星看成点，就可以用点动成线来解释卫星在预定轨道飞行留下的痕迹了．
【解答】解：把卫星看成点，则卫星在预定轨道飞行留下的痕迹体现了点动成线．
故选：A．
【点评】本题考查了点、线、面、体的知识点，理解点动成线、线动成面、面动成体是解题的关键．
3．（3分）2024的相反数等于（ ）
A．﹣2024B．2024C．D．
【答案】A
【分析】根据符号不同，绝对值相同的两个数互为相反数即可求得答案．
【解答】解：2024的相反数是﹣2024．
故选：A．
【点评】本题考查了相反数的概念，掌握只有符号不同的两个数叫做互为相反数是解答此题的关键．
4．（3分）下列四个数中，绝对值最大的是（ ）
A．2B．C．0D．﹣3
【答案】D
【分析】分别计算出四个选项的绝对值，然后再进行比较，找出绝对值最大的选项．
【解答】解：A、|2|＝2；B、|﹣|＝；C、|0|＝0；D、|﹣3|＝3；
∵0＜＜2＜3，
∴四个数中绝对值最大的是﹣3．
故选：D．
【点评】绝对值规律总结：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．
5．（3分）如果|a+2|+|b﹣1|＝0，那么（a+b）2023的值为（ ）
A．﹣2023B．2023C．﹣1D．1
【答案】C
【分析】先根据非负数的性质求出a和b的值，再代入代数式进行计算即可．
【解答】解：∵|a+2|+|b﹣1|＝0，
∴a+2＝0，b﹣1＝0，
∴a＝﹣2，b＝1，
∴（a+b）2023＝（﹣2+1）2023＝（﹣1）2023＝﹣1，
故选：C．
【点评】本题考查了非负数的性质，以及求代数式的值，根据非负数的性质求出a和b的值是解答本题的关键．
6．（3分）若代数2x2+3x的值为5，则代数式4x2+6x﹣9的值是（ ）
A．1B．﹣1C．4D．﹣4
【答案】A
【分析】将代数式适当变形后，利用整体代入的方法解答即可．
【解答】解：∵2x2+3x的值为5，
∴2x2+3x＝5，
∴原式＝2（2x2+3x）﹣9
＝2×5﹣9
＝10﹣9
＝1．
故选：A．
【点评】本题主要考查了求代数式的值，将代数式适当变形后，利用整体代入的方法解答是解题的关键．
7．（3分）我们规定一种新运算“★”，其含义：对于有理数a，b，a★b＝a2﹣ab﹣b，则计算（﹣3）★（﹣1）的结果是（ ）
A．﹣11B．5C．7D．13
【答案】C
【分析】根据新运算“★”的定义式，代入数据即可求出结论．
【解答】解：（﹣3）★（﹣1）＝（﹣3）2﹣（﹣3）×（﹣1）﹣（﹣1）＝9﹣3+1＝7．
故选：C．
【点评】本题考查了有理数的混合运算，牢记有理数混合运算的运算顺序是解题的关键．
8．（3分）“幻方”最早记载于春秋时期的《大戴礼记》中，现将数字1～9填入如图所示的“幻方”中，使得每个圆圈上的四个数字的和都等于21，若每个圆圈上的四个数字的平方和分别记A、B、C，且A+B+C＝411．如果将交点处的三个圆圈填入的数字分别记作为x、y、x+y，则xy的值为（ ）
A．6B．10C．14D．18
【答案】D
【分析】每个圆圈上的四个数字的和都等于21，则三个大圆圈上的数字之和为63，可得x+y＝9，由于A+B+C＝411，进而得x2+y2＝81﹣2xy，再结合x+y＝9即可解决问题．
【解答】解：∵每个圆圈上的四个数字的和都等于21，
∴三个大圆圈上的数字之和为：21×3＝63，
∵各小圆圈的数字之和为：1+2+3+4+5+6+7+8+9＝45，
为什么63≠45，这是因为x、y、x+y都加了两次，
∴x+y+x+y＝63﹣45，
∴2x+2y＝18，
∴x+y＝9，
∵A+B+C＝411，
而各圆圈的数字的平方和为12+22+32+42+52+62+72+82+92＝285，
为什么411≠285呢？
这是因为三角形各顶点处三个圆圈内的数字的平方都加了两次，
∴（x+y）2+x2+y2＝411﹣285＝126，
∴x2+2xy+y2+x2+y2＝156，
∴2（x2+y2+xy）＝126，
∴x2+y2+xy＝63，
∵x+y＝9，
∴（x+y）2＝92，
∴x2+2xy+y2＝81，
∴x2+y2＝81﹣2xy，
将x2+y2＝81﹣2xy代入x2+y2+xy＝63得81﹣2xy+xy＝63，
∴﹣xy＝81﹣63＝18，
∴xy＝18．
故选：D．
【点评】本题考查有理数的乘方和加法运算，整式的运算，乘法公式，掌握有理数的乘方和加法运算法则，以及整式运算法则和乘法公式是解题的关键．
二、填空题（共5小题，每小题3分，共15分）
9．（3分）五•一节期间，某景区共接约游客约1250000人次，将“1250000”用科学记数法是为 1.25×106 ．
【答案】1.25×106．
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．
【解答】解：将“1250000”用科学记数法表示为1.25×106．
故答案为：1.25×106．
【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
10．（3分）﹣的倒数等于 ﹣ ．
【答案】见试题解答内容
【分析】先把待分数化为假分数，然后根据倒数的定义求解．
【解答】解：﹣1＝﹣，
﹣的倒数为﹣．
故答案为﹣．
【点评】本题考查了倒数的定义：a（a≠0）的倒数为．
11．（3分）若3a2bn与4amb4是同类项，则mn＝ 16 ．
【答案】见试题解答内容
【分析】根据同类项：所含字母相同，并且相同字母的指数也相同，可得出m、n的值，代入代数式计算即可．
【解答】解：∵3a2bn与4amb4是同类项，
∴m＝2，n＝4，
故mn＝24＝16．
故答案为：16．
【点评】本题考查了同类项的知识，属于基础题，掌握同类项中的两个相同是关键，①所含字母相同，②相同字母的指数相同．
12．（3分）有一个正方体，六个面上分别写有数字1，2，3，4，5，6，如图是我们能看到的三种情况，如果记6的对面数字为a，2的对面数字为b，那么a+b的值为 7 ．
【答案】见试题解答内容
【分析】由平面图形的折叠及立体图形的表面展开图的特点得出a和b的值，然后相加即可得出答案．
【解答】解：根据给出的图形可得：6的对面数字为3，2的对面数字为4，
则a＝3，b＝4，
所以a+b的值为7；
故答案为：7．
【点评】本题考查了展开图折成几何体，注意正方体的空间图形，从相对面入手，分析及解答问题．
13．（3分）如图所示，将形状、大小完全相同的“•”和线段按照一定规律摆成下列图形，第1幅图形中“•”的个数为 a1，第2幅图形中“•”的个数 a2，第3幅图形中“•”的个数为 a3，…以此类推，则+…+的值为 ．
【答案】．
【分析】先根据图形得出a1＝3＝1×3，a2＝8＝2×4，a3＝15＝3×5，a4＝24＝4×6，…，an＝n（n+2），再代入、裂项求解即可．
【解答】解：∵a1＝3＝1×3，a2＝8＝2×4，a3＝15＝3×5，a4＝24＝4×6，…，an＝n（n+2）；
∴+…+
＝+++…+
＝×（1﹣+++…+）
＝×（1+﹣﹣）
＝×
＝，
故答案为：．
【点评】本题主要考查图形的变化规律，解决这类问题首先要从简单图形入手，抓住随着“编号”或“序号”增加时，后一个图形与前一个图形相比，在数量上增加（或倍数）情况的变化，找出数量上的变化规律，从而推出一般性的结论．
三.解答题（共7小题，共61分）
14．（16分）计算：
（1）2+（﹣9）﹣（﹣3）+5；
（2）﹣24÷（﹣4）×（﹣）；
（3）；
（4）﹣32﹣（5﹣7）×6+（﹣2）3÷8．
【答案】（1）1；
（2）﹣；
（3）﹣8；
（4）2．
【分析】（1）利用有理数的加减法则计算即可；
（2）利用有理数的乘除法则计算即可；
（3）利用乘法分配律计算即可；
（4）先算乘方及括号里面的，再算乘除，最后算加减即可．
【解答】解：（1）原式＝﹣7+3+5
＝﹣4+5
＝1；
（2）原式＝6×（﹣）
＝﹣；
（3）原式＝×（﹣12）﹣×（﹣12）+×（﹣12）
＝﹣6+2﹣4
＝﹣8；
（4）原式＝﹣9﹣（﹣2）×6+（﹣8）÷8
＝﹣9+12﹣1
＝2．
【点评】本题考查有理数的混合运算，熟练掌握相关运算法则是解题的关键．
15．（6分）化简求值：2（3a2b﹣ab2）﹣3（2a2b﹣ab2+ab），其中a＝，b＝﹣2．
【答案】见试题解答内容
【分析】原式去括号合并得到最简结果，把a与b的值代入计算即可求出值．
【解答】解：原式＝6a2b﹣2ab2﹣6a2b+3ab2﹣3ab
＝（6a2b﹣6a2b）+（﹣2ab2+3ab2）﹣3ab
＝ab2﹣3ab，
当，b＝﹣2时
原式＝ab2﹣3ab
＝
＝2+3
＝5．
【点评】此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．
16．（8分）如图是由棱长都为1cm的6块小正方体组成的简单几何体．
（1）请在方格中画出该几何体的三个视图．
（2）如果在这个几何体上再添加一些小正方体，并保持主视图和左视图不变，最多可以再添加 2 块小正方体，
【答案】（1）见解答；
（2）2．
【分析】（1）根据简单组合体三视图的画法画出相应的图形即可；
（2）在俯视图上相应位置备注出相应摆放的数目即可．
【解答】解：（1）该几何体的主视图、左视图和俯视图如下：
（2）在备注数字的位置加摆相应数量的小正方体，
所以最多可以添加2个，
故答案为：2．
【点评】本题考查简单组合体的三视图，理解视图的意义是正确解答的前提．
17．（7分）元旦放假时，小明一家三口一起乘小轿车去乡下探望爷爷、奶奶和外公、外婆．早上从家里出发，向东走了6千米到超市买东西，然后又向东走了1.5千米到爷爷家，中午从爷爷家出发向西走了12千米到外公家，晚上返回家里．
（1）若以家为原点，向东为正方向，用1个单位长度表示1千米，请将超市、爷爷家和外公家的位置在下面数轴上分别用点A、B、C表示出来；
（2）问超市A和外公家C相距多少千米？
（3）若小轿车每千米耗油0.08升，求小明一家从出发到返回家所经历路程小车的耗油量．（精确到0.1升）
【答案】见试题解答内容
【分析】（1）根据数轴是表示数的直线，可用数轴上的点表示数；
（2）根据有理数的减法和绝对值的性质，可得答案；
（3）根据单位耗油量乘以行驶路程，可得耗油量．
【解答】解：（1）点A、B、C如图所示：
（2）AC＝|6﹣（﹣4.5）|＝10.5（千米）．
故超市A和外公家C相距10.5千米．
（3）6+1.5+12+4.5＝24（千米），
24×0.08＝1.92≈1.9（升）．
答：小明一家从出发到返回家所经历路程小车的耗油量约为1.9升．
【点评】本题考查了有理数的加减，数轴的应用，关键是能根据题意列出算式．其中第（3）小题中小轿车行驶的路程是从家里出发到超市，再到爷爷家，再从爷爷家到外公家，晚上返回家里的路程和．
18．（6分）如图是一个“数值转换机”（箭头是指数进入转换机的路径，方框是对进入的数进行转换的转换机）．
（1）当小明输入4，7这两个数时，则两次输出的结果依次为 1 ， 2 ；
（2）你认为当输入数等于 0 时（写出一个即可），其输出结果为0；
（3）你认为这个“数值转换机”不可能输出 负 数；
（4）有一次，小明操作的时候，输出的结果是2，聪明的你判断一下，小明输入的正整数是 5n+2 （用含自然数n的代数式表示）．
【答案】见试题解答内容
【分析】（1）分别将4、7代入数值转换机，计算即可得到输出结果；
（2）当输入数字为0得到结果为0；
（3）数值转换机不可能输出负数；
（4）根据数轴转换机的规律表示出结果即可．
【解答】解：（1）若输入的数字为4时，4＞2，得到4+（﹣5）＝﹣1，
﹣1＜2，得到相反数为1，倒数为1，输出结果为1；
若输入数字为7时，7＞2，得到7+（﹣5）＝2，
得到相反数为﹣2，绝对值为2，输出结果为2；
（2）根据题意得：输入数字为0（5、10、15…5的倍数均可），结果为0；
（3）这个“数值转换机”不可能输出负数；
（4）归纳总结得：小明输入的正整数是5n+2．
故答案为：1，2；0；负；5n+2．
【点评】此题考查了倒数、相反数和绝对值的知识，弄清题中的图表表示的意义是解本题的关键．
19．（9分）我国南宋时期杰出的数学家杨辉是钱塘人，如图所示的图表是他在《详解九章算法》中记载的“杨辉三角”．
此图揭示了（a+b）n（n为非负整数）的展开式的项数及各项系数的有关规律，由此规律可解决如下问题：
（1）请在图中括号内的数为 6 ；
（2）（a+b）20展开式共有 21 项，第19项系数为 190 ；
（3）根据上面的规律，写出（a+b）6的展开式： a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6 ；
（4）利用上面的规律计算：35﹣5×34+10×33﹣10×32+5×3﹣1；
（5）假如今天是星期五，那么再过621天是星期几？（写过程）
【答案】（1）6；（2）21；190；（3）a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6；（4）32；（5）四．
【分析】（1）根据表中数据特点解题即可；
（2）罗列后按照规律（a+b）n展开式中共有（n+1）项，当n≥3时，倒数第三项的系数是 ，代入数据计算即可；
（3）根据图示顺推即可得到（a+b）6展开式；
（4）根据（a+b）5展开式，令a＝3，b＝﹣1时代入展开式即可得到所求代数式的值；
（5）将621变形为（7﹣1）21展开后前21项和是7的倍数，所以 621除7结果的余数为6，则有假如今天是星期五，那么再过 621天是星期四．
【解答】解：（1）图中括号内的数为3+3＝6，
故答案为：6；
（2）（a+1）1＝a+b，展开式有1+1＝2项；
（a+b）2＝a2+2ab+b2，展开式有 2+1＝3项，倒数第三项系数为；
（a+b）3＝a3+3a2b+3ab2+b3，展开式有 3+1＝4项，倒数第三项系数为 ；
（a+b）4＝a4+4a3b+6a2b2+4ab3+b4，展开式有4+1＝5项，倒数第三项系数为；
（a+b）5＝a5+5a4b+10a3b2+10a2b3+5ab4+b5展开式有5+1＝6项，倒数第三项系数为 ；
……；
以此类推，（a+b）n展开式中共有（n+1）项，当n≥3时，倒数第三项的系数 ；
∴（a+b）20展开式共有21项，第19项系数为 ；
故答案为：21；190；
（3）根据图示，（a+b）6＝a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6
故答案为：a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6；
（4）∵（a+b）5＝a5+5a4b+10a3b2+10a2b3+5ab4+b5
∴当a＝3，b＝﹣1时，（3﹣1）5＝35﹣5×34+10×33﹣10×32+5×3﹣1，
∴35﹣5×34+10×33﹣10×32+5×3﹣1＝32；
（5）621＝（7﹣1）21＝721﹣a•720+b•719﹣c•718+⋯+r•72﹣s•7﹣1
（a、b、c、r、s是一列常数），
∴721﹣a•720+b•719﹣c•718+•．+r•72﹣s•7，
刚好是7的整数倍，
∴621除7结果的余数为6，
∴假如今天是星期五，那么再过621天是星期四．
【点评】本题考查了数字的变化规律，罗列分析出规律是解答本题的关键．
20．（9分）将一条数轴在原点O和点B处各折一下，得到如图所示的“折线数轴”，图中点A表示﹣10，点B表示10，点C表示18．我们称点A和点C在数轴上的“友好距离”为28个单位长度．动点P从点A出发，以2单位长度/秒的速度沿着“折线数轴”向其正方向运动．当运动到点O与点B之间时速度变为原来的一半．经过点B后立刻恢复原速；同时，动点Q从点C出发，以1单位长度/秒的速度沿着“折线数轴”向其负方向运动，当运动到点B与点O之间时速度变为原来的两倍，经过O后也立刻恢复原速．设运动的时间为t秒．
（1）动点P从点A运动至点C需要 19 秒，动点Q从点C运动至点A需要 23 秒；
（2）P，Q两点相遇时，求出相遇点M在“折线数轴”上所对应的数；
（3）是否存在t值，使得点P和点Q在“折线数轴”上的“友好距离”等于点A和点B在“折线数轴”上的“友好距离”？若存在，求出t的值；若不存在，请说明理由．
【答案】见试题解答内容
【分析】（1）根据题意可得，动点P从点A运动至点C需要的时间是：10÷2+10÷1+8÷2＝19（s），动点Q从点C运动至点A需要的时间是：8÷1+10÷2+10÷1＝23（s）；
（2）根据题意可知，P、Q两点在OB上相遇，P点运动到OB上时表示的数是t﹣5，Q点运动到OB上时表示的数是10﹣2（t﹣8），则t﹣5＝10﹣2（t﹣8），求出t的值，再求M点表示的数即可；
（3）分7种情况讨论：①当0≤t≤5时，P点在OA上，Q点在BC上，此时P点表示的数是﹣10+2t，Q点表示的数是18﹣t，由题意可得，28﹣3t＝20，解得t＝；②当5＜t≤8时，P点在OB上，Q点在BC上，此时P点表示的数是t﹣5，Q点表示的数是18﹣t，由题意可得，23﹣2t＝20，解得t＝（舍）；③8＜t≤13时，点P、Q都在BO上，此时PQ＜10，此情况不符合题意；④13＜t≤15时，P点在OB上，Q点在OA上，此时P点表示的数是t﹣5，Q点表示的数是13﹣t，由题意可得，2t﹣18＝20，解得t＝19（舍）；⑤15＜t≤19时，P点在BC上，Q点在OA上，此时P点表示的数是2t﹣20，Q点表示的数是13﹣t，由题意可得，3t﹣33＝20，解得t＝；⑥19＜t≤23时，P点在C的右侧，Q点在OA上，此时P点表示的数是2t﹣20，Q点表示的数是13﹣t，由题意可得，3t﹣33＝20，解得t＝（舍）；⑦t＞23时，P点在C点右侧，Q点在A点左侧，PQ＞20，不符合题意．
【解答】解：（1）∵点A表示﹣10，点B表示10，点C表示18，
∴OA＝10，BO＝10，BC＝8，
∴动点P从点A运动至点C需要的时间是：10÷2+10÷1+8÷2＝19（s），
动点Q从点C运动至点A需要的时间是：8÷1+10÷210÷1＝23（s），
故答案为：19，23；
（2）根据题意可知，P、Q两点在OB上相遇，
P点运动到OB上时表示的数是t﹣5，Q点运动到OB上时表示的数是10﹣2（t﹣8），
∴t﹣5＝10﹣2（t﹣8），
解得t＝，
∴M点表示的数是﹣5＝；
（3）存在t值，使得点P和点Q在“折线数轴”上的“友好距离”等于点A和点B在“折线数轴”上的“友好距离”，理由如下：
∵点A表示﹣10，点B表示10，
∴点A和点B在“折线数轴”上的“友好距离”是20，
①当0≤t≤5时，P点在OA上，Q点在BC上，
此时P点表示的数是﹣10+2t，Q点表示的数是18﹣t，
∴点P和点Q在“折线数轴”上的“友好距离”为18﹣t+10﹣2t＝28﹣3t，
由题意可得，28﹣3t＝20，
解得t＝；
②当5＜t≤8时，P点在OB上，Q点在BC上，
此时P点表示的数是t﹣5，Q点表示的数是18﹣t，
∴点P和点Q在“折线数轴”上的“友好距离”为18﹣t﹣t+5＝23﹣2t，
由题意可得，23﹣2t＝20，
解得t＝（舍）；
③8＜t≤13时，点P、Q都在BO上，此时PQ＜10，
∴此情况不符合题意；
④13＜t≤15时，P点在OB上，Q点在OA上，
此时P点表示的数是t﹣5，Q点表示的数是13﹣t，
∴点P和点Q在“折线数轴”上的“友好距离”为t﹣5﹣13+t＝20；t＝19（舍）；
⑤15＜t≤19时，P点在BC上，Q点在OA上，
此时P点表示的数是2t﹣20，Q点表示的数是13﹣t，
∴点P和点Q在“折线数轴”上的“友好距离”为2t﹣20﹣13+t＝3t﹣33，
由题意可得，3t﹣33＝20，
解得t＝；
⑥19＜t≤23时，P点在C的右侧，Q点在OA上，
此时P点表示的数是2t﹣20，Q点表示的数是13﹣t，
∴点P和点Q在“折线数轴”上的“友好距离”为（2t﹣20）﹣（13﹣t）＝3t﹣33，
由题意可得，3t﹣33＝20，
解得t＝（舍）；
⑦t＞23时，P点在C点右侧，Q点在A点左侧，PQ＞20，不符合题意；
综上所述：t的值为或．
【点评】本题考查实数与数轴，熟练掌握实数上点与数轴的对应关系，弄清“友好函数”的定义是解题的关键．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2024/11/26 1:07:18；用户：18328501451；邮箱：18328501451；学号：43314264