江苏省淮安市集团校2024-2025学年八年级上学期期中数学试卷

这是一份江苏省淮安市集团校2024-2025学年八年级上学期期中数学试卷，共25页。试卷主要包含了选择题.，填空题，解答题等内容，欢迎下载使用。
1．（3分）“二十四节气”是中华农耕文明的智慧结晶，下面四幅作品分别代表“立春”、“芒种”、“白露”、“大雪”，其中是轴对称图形的是（ ）
A．B．
C．D．
2．（3分）下列实数中，是无理数的是（ ）
A．2.4B．C．D．
3．（3分）下列各组数是勾股数的是（ ）
A．4，5，6B．5，12，13
C．0.3，0.4，0.5D．8，24，25
4．（3分）等腰三角形的一个底角是50°，则它的顶角是（ ）
A．50°B．50°或65°C．65°D．80°
5．（3分）估算的值在（ ）
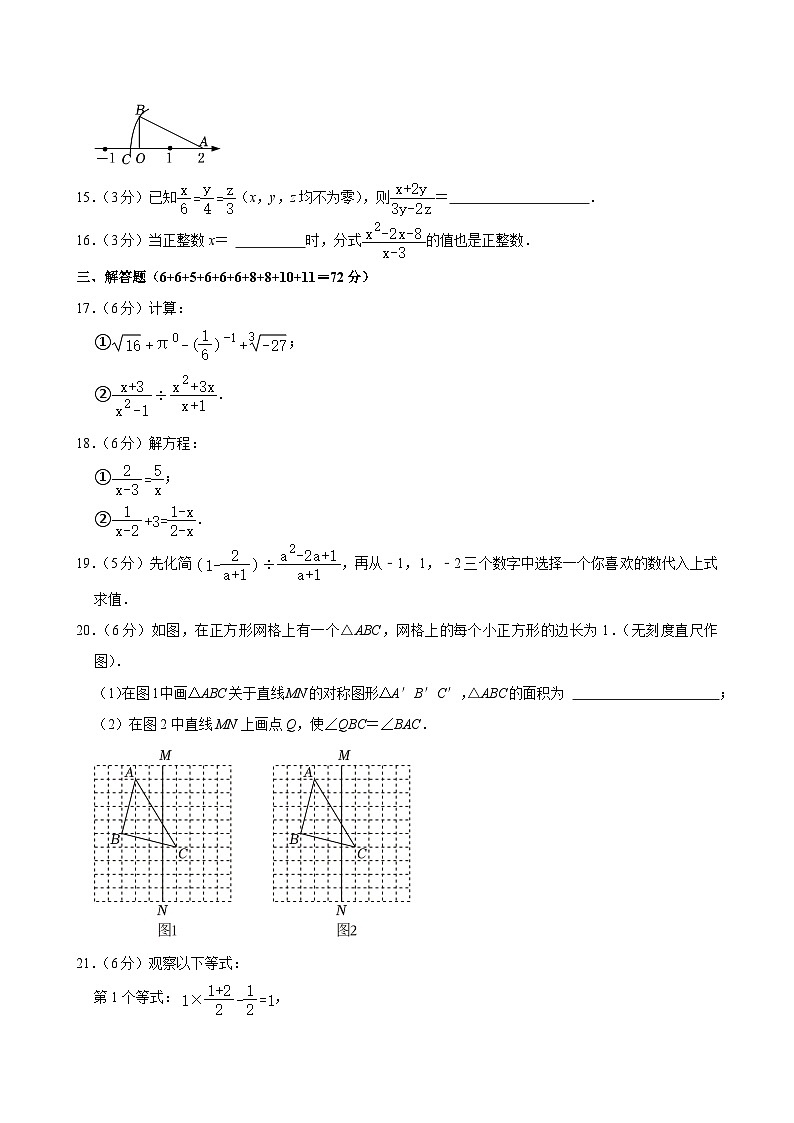
A．1与2之间B．2与3之间C．3与4之间D．4与5之间
6．（3分）将分式中的m、n都扩大为原来的3倍，则分式的值（ ）
A．不变B．是原来的3倍
C．是原来的9倍D．是原来的6倍
7．（3分）如图，AD是△ABC的角平分线，DE⊥AB，垂足为E，S△ABC＝36，DE＝4，AB＝10，则AC长为（ ）
A．10B．8C．6D．4
8．（3分）如图，∠BAC＝90°，点B是射线AM上的一个动点，点C是射线AN上的一个动点，且线段BC的长度不变，D是点A关于直线BC的对称点，连接AD，若2AD＝BC．则∠ACD的度数是（ ）
A．30°B．150°C．30°或150°D．不确定
二、填空题（本大题共8小题，每小题3分，共24分）
9．（3分）用四舍五入法将7.385精确到0.01，所得的近似数为 ．
10．（3分）使分式有意义的x的取值范围是 ．
11．（3分）已知某正数的两个不同平方根分别是m+4和2m﹣16，则m＝ ．
12．（3分）如图，在△ABC中，分别以点A和点B为圆心，大于AB的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD．若△ADC的周长为10，AB＝7，则△ABC的周长为 ．
13．（3分）由于木质衣架没有柔性，在挂置衣服的时候不太方便操作．小敏设计了一种衣架，在使用时能轻易收拢，然后套进衣服后松开即可．如图1，衣架杆OA＝OB＝18cm，若衣架收拢时，∠AOB＝60°，如图2，则此时A，B两点之间的距离是 cm．
14．（3分）如图，数轴上的点O表示的数是0，点A表示的数是2，OB⊥OA，垂足为O，且OB＝1，以A为圆心，AB长为半径画弧，交数轴于点C，则点C表示的数为 ．
15．（3分）已知（x，y，z均不为零），则＝ ．
16．（3分）当正整数x＝ 时，分式的值也是正整数．
三、解答题（6+6+5+6+6+6+8+8+10+11＝72分）
17．（6分）计算：
①；
②．
18．（6分）解方程：
①；
②．
19．（5分）先化简，再从﹣1，1，﹣2三个数字中选择一个你喜欢的数代入上式求值．
20．（6分）如图，在正方形网格上有一个△ABC，网格上的每个小正方形的边长为1．（无刻度直尺作图）．
（1）在图1中画△ABC关于直线MN的对称图形△A′B′C′，△ABC的面积为 ；
（2）在图2中直线MN上画点Q，使∠QBC＝∠BAC．
21．（6分）观察以下等式：
第1个等式：，
第2个等式：，
第3个等式：，
第4个等式：，
第5个等式：，
……
按照以上规律．解决下列问题：
（1）写出第6个等式： ；
（2）写出你猜想的第n个等式（用含n的式子表示），并证明．
22．（6分）如图，在△ABC中，AB＝AC，点D在BC上，DE⊥AB，DF⊥AC，垂足分别为E、F，且DE＝DF．求证：D是BC的中点．
23．（8分）如图，在△ABC中，AB＝5cm，BC＝a cm，AC＝b cm，且，动点P从点C出发沿射线CB以2cm/s的速度运动，设运动时间为t（s）．
（1）判断△ABC的形状并说明理由；
（2）当t＝ 时，△ABP是等腰三角形？（请直接写出答案）
24．（8分）根据市场需求，某小型企业为加快生产速度，需要更新生产设备，更新设备后生产效率比更新前提高了25%，设更新设备前每天生产x件产品．解答下列问题：
（1）更新设备后每天生产 件产品（用含x的式子表示）；
（2）更新设备前生产2500件产品比更新设备后生产3000件产品多用1天，求更新设备后每天生产多少件产品．
25．（10分）勾股定理具有丰富的文化内涵，它揭示了直角三角形的三边关系，搭建起几何与代数之间的桥梁，为解决几何问题拓宽了思路．请完成下面问题：
（1）如图1，请你用两种不同方法表示梯形ABCD的面积，从而验证勾股定理．
（2）如图2，在直线l的同侧有两个点C、D，已知点C和点D到直线l的距离分别为2和5，且，现要在直线l上取点P，使得PD+PC的值最小．
①请用无刻度直尺和圆规在图2中确定点P的位置（要求：尺规作图，保留作图痕迹，不写作法）
②直接写出PC+PD的最小值为 ；
（3）借助上面的思考过程，直接写出的最小值为 ．
26．（11分）如图，在长方形ABCD中，∠DAB＝∠B＝∠C＝∠D＝90°，AB＝CD＝10，AD＝BC＝4，AB∥CD，AD∥BC．N是边CD上一点，CN＝2．若M为AB边上一个动点，将四边形BCNM沿MN折叠，点B、C的对应点分别为点B′、C′，若线段MB'与边CD交于点E．
（1）如图1，证明：△EMN为等腰三角形；
（2）如图2，当点M与点A重合时，求线段DE的长；
（3）点M从点A向点B运动的过程中，
①线段DE的最大值为 ；
②请直接写出点E运动的路径长为 ．
2024-2025学年江苏省淮安市集团校八年级（上）期中数学试卷
参考答案与试题解析
一、选择题（本大题共8小题，每小题3分，共24分）.
1．（3分）“二十四节气”是中华农耕文明的智慧结晶，下面四幅作品分别代表“立春”、“芒种”、“白露”、“大雪”，其中是轴对称图形的是（ ）
A．B．
C．D．
【答案】D
【分析】根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
【解答】解：A，B，C选项中的图形都不能找到一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；
D选项中的图形能找到一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形．
故选：D．
【点评】本题考查了轴对称图形的概念，熟知轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合是解题的关键．
2．（3分）下列实数中，是无理数的是（ ）
A．2.4B．C．D．
【答案】D
【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
【解答】解：A．2.4是有限小数，属于有理数，故本选项不符合题意；
B．＝﹣2，是整数，属于有理数，故本选项不符合题意；
C．是分数，属于有理数，故本选项不符合题意；
D．是无理数，故本选项符合题意．
故选：D．
【点评】此题主要考查了无理数，立方根以及算术平方根，关键掌握初中范围内学习的无理数有：π，2π等；开方开不尽得到的数；以及像0.1010010001…（两个1之间依次多一个0）等有这样规律的数．
3．（3分）下列各组数是勾股数的是（ ）
A．4，5，6B．5，12，13
C．0.3，0.4，0.5D．8，24，25
【答案】B
【分析】根据勾股数的定义逐项判断即可．
【解答】解：A．42+52≠62，这组数据不是勾股数，故选项A不符合题意；
B．52+122＝132，这组数据是勾股数，故选项B符合题意；
C．0.3、0.4，0.5不是正整数，这组数据不是勾股数，故选项C不符合题意；
D．82+242≠252，这组数据不是勾股数，故选项D不符合题意；
故选：B．
【点评】本题考查了勾股数，熟练掌握勾股数的定义是解题的关键．
4．（3分）等腰三角形的一个底角是50°，则它的顶角是（ ）
A．50°B．50°或65°C．65°D．80°
【答案】D
【分析】由等腰三角形的性质可知两底角相等，再根据三角形内角和为180°，即可求出顶角的度数．
【解答】解：∵等腰三角形的一个底角是50°，
∴它的顶角＝180°﹣50°﹣50°＝80°，
故选：D．
【点评】本题考查了等腰三角形的性质以及三角形内角和定理的运用，解题的关键是熟记等腰三角形的各种性质并且能够灵活运用．
5．（3分）估算的值在（ ）
A．1与2之间B．2与3之间C．3与4之间D．4与5之间
【答案】A
【分析】根据算术平方根的定义估算无理数的大小，进而得到﹣2的大小即可．
【解答】解：∵9＜15＜16，
∴＜＜，即3＜＜4，
∴1＜﹣2＜2，
故选：A．
【点评】本题考查估算无理数的大小，掌握算术平方根的定义是正确解答的关键．
6．（3分）将分式中的m、n都扩大为原来的3倍，则分式的值（ ）
A．不变B．是原来的3倍
C．是原来的9倍D．是原来的6倍
【答案】B
【分析】将分式中的m、n都扩大为原来的3倍并化简即可．
【解答】解：根据题意，得＝＝，
∴将分式中的m、n都扩大为原来的3倍，则分式的值是原来的3倍．
故选：B．
【点评】本题考查分式的基本性质，掌握分式的基本性质是解题的关键．
7．（3分）如图，AD是△ABC的角平分线，DE⊥AB，垂足为E，S△ABC＝36，DE＝4，AB＝10，则AC长为（ ）
A．10B．8C．6D．4
【答案】B
【分析】过点D作DF⊥AC于F，然后利用△ABC的面积公式列式计算即可得解．
【解答】解：如图，过点D作DF⊥AC于F，
∵AD是△ABC的角平分线，DF⊥AC，DE⊥AB，
∴DE＝DF＝4，
∵S△ABC＝S△ABD+S△ADC＝36，
∴AB•DE+AC•DF＝36，
∵AB＝10，
∴×10×4+AC×4＝36，
∴AC＝8，
故选：B．
【点评】本题考查了角平分线的性质，三角形的面积，熟练掌握角平分线的性质是解题的关键．
8．（3分）如图，∠BAC＝90°，点B是射线AM上的一个动点，点C是射线AN上的一个动点，且线段BC的长度不变，D是点A关于直线BC的对称点，连接AD，若2AD＝BC．则∠ACD的度数是（ ）
A．30°B．150°C．30°或150°D．不确定
【答案】C
【分析】分两种情况，取BC的中点E，连接AE，DE，依据直角三角形斜边上中线的性质，即可得到△ADE是等边三角形，进而依据轴对称的性质得出∠ACD的度数．
【解答】解：分两种情况：
如图，当AB＞AC时，取BC的中点E，连接AE，DE，
则AE＝DE＝BC．即BC＝2AE＝2DE，
又∵BC＝2AD，
∴AD＝AE＝DE，
∴△ADE是等边三角形，
∴∠AED＝60°，
又∵BC垂直平分AD，
∴∠AEC＝30°，
又∵BE＝AE，
∴∠ABC＝∠AEC＝15°，
∴∠ACB＝90°﹣15＝75°，
∴∠ACD＝2∠ACB＝150°；如图，当AB＜AC时，同理可得∠ACD＝30°，
又∵∠BAC＝∠BDC＝90°，
∴∠ABD＝150°，
故选：C．
【点评】本题主要考查了轴对称的性质的运用，如果两个图形关于某直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线．
二、填空题（本大题共8小题，每小题3分，共24分）
9．（3分）用四舍五入法将7.385精确到0.01，所得的近似数为 7.39 ．
【答案】7.39．
【分析】对千分位数字四舍五入即可．
【解答】解：用四舍五入法将7.385精确到0.01，所得的近似数为7.39，
故答案为：7.39．
【点评】本题主要考查近似数，解题的关键是掌握四舍五入法．
10．（3分）使分式有意义的x的取值范围是 x≠﹣1 ．
【答案】x≠﹣1．
【分析】根据分式的分母不为0列出不等式，解不等式得到答案．
【解答】解：由题意得：x+1≠0，
解得：x≠﹣1，
故答案为：x≠﹣1．
【点评】本题考查的是分式有意义的条件，掌握分式的分母不为0是解题的关键．
11．（3分）已知某正数的两个不同平方根分别是m+4和2m﹣16，则m＝ 4 ．
【答案】见试题解答内容
【分析】利用一个正数的平方根有两个，且互为相反数得，m+4+2m﹣16＝0，解关于m的一元一次方程即可．
【解答】解：∵正数的两个不同平方根分别是m+4和2m﹣16，
∴m+4+2m﹣16＝0．
解得m＝4．
故答案为：4．
【点评】本题考查了平方根的性质，一个正数有两个平方根，且它们互为相反数．
12．（3分）如图，在△ABC中，分别以点A和点B为圆心，大于AB的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD．若△ADC的周长为10，AB＝7，则△ABC的周长为 17 ．
【答案】见试题解答内容
【分析】首先根据题意可得MN是AB的垂直平分线，由线段垂直平分线的性质可得AD＝BD，再根据△ADC的周长为10可得AC+BC＝10，又由条件AB＝7可得△ABC的周长．
【解答】解：∵在△ABC中，分别以点A和点B为圆心，大于AB的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD．
∴MN是AB的垂直平分线，
∴AD＝BD，
∵△ADC的周长为10，
∴AC+AD+CD＝AC+BD+CD＝AC+BC＝10，
∵AB＝7，
∴△ABC的周长为：AC+BC+AB＝10+7＝17．
故答案为17．
【点评】此题考查了线段垂直平分线的性质与作法．题目难度不大，解题时要注意数形结合思想的应用．
13．（3分）由于木质衣架没有柔性，在挂置衣服的时候不太方便操作．小敏设计了一种衣架，在使用时能轻易收拢，然后套进衣服后松开即可．如图1，衣架杆OA＝OB＝18cm，若衣架收拢时，∠AOB＝60°，如图2，则此时A，B两点之间的距离是 18 cm．
【答案】见试题解答内容
【分析】根据有一个角是60°的等腰三角形的等边三角形进行解答即可．
【解答】解：∵OA＝OB，∠AOB＝60°，
∴△AOB是等边三角形，
∴AB＝OA＝OB＝18cm，
故答案为：18
【点评】此题考查等边三角形问题，关键是根据有一个角是60°的等腰三角形的等边三角形进行分析．
14．（3分）如图，数轴上的点O表示的数是0，点A表示的数是2，OB⊥OA，垂足为O，且OB＝1，以A为圆心，AB长为半径画弧，交数轴于点C，则点C表示的数为 2﹣ ．
【答案】2﹣．
【分析】根据勾股定理求出AB的长，得到AC的长，从而得到点C表示的数．
【解答】解：根据勾股定理得：AB＝＝＝，
∵以A为圆心，AB长为半径画弧，交数轴于点C，
∴AC＝AB＝，
∴点C表示的数为2﹣，
故答案为：2﹣．
【点评】本题考查了数轴，勾股定理，掌握在直角三角形中，两条直角边的平方和等于斜边的平方是解题的关键．
15．（3分）已知（x，y，z均不为零），则＝ ．
【答案】．
【分析】根据已知条件可设x＝6k，则y＝4k，z＝3k，将其代入所求分式，计算即可．
【解答】解：∵（x，y，z均不为零），
∴设x＝6k，则y＝4k，z＝3k，
∴＝＝＝．
故答案为：．
【点评】本题考查了比例的性质，解此类题可根据分式的基本性质先用未知数k表示出x，y，z，再代入计算．
16．（3分）当正整数x＝ 2或8 时，分式的值也是正整数．
【答案】2或8．
【分析】根据分式的值的定义以及结果是正整数进行计算即可．
【解答】解：原式＝
＝
＝x+1﹣，
∵分式的值是正整数，x也是正整数，
∴是整数，
∴x﹣3＝±1，x﹣3＝±5，
解得x＝4或x＝2或x＝8或x＝﹣2（舍去），
当x＝4时，分式x+1﹣＝4+1﹣5＝0（不符合题意舍去），
故答案为：2或8．
【点评】本题考查分式的值，理解分式值的定义是正确解答的关键．
三、解答题（6+6+5+6+6+6+8+8+10+11＝72分）
17．（6分）计算：
①；
②．
【答案】①﹣4；
②．
【分析】①先根据算术平方根、零指数幂、负整数指数幂、立方根的定义计算，再根据有理数加减法则计算即可；
②先把分式的分子、分母分解因式，再把除法运算化为乘法运算，约分即可．
【解答】解：①
＝4+1﹣6+（﹣3）
＝﹣4；
②
＝
＝
＝．
【点评】本题考查了实数的运算，分式的乘除，熟练掌握运算法则是解题的关键．
18．（6分）解方程：
①；
②．
【答案】①x＝5；
②无解．
【分析】利用去分母将原方程化为整式方程，解方程求得x的值后进行检验即可．
【解答】解：①原方程去分母得：2x＝5x﹣15，
解得：x＝5，
检验：当x＝5时，x（x﹣3）≠0，
故原方程的解为x＝5；
②原方程去分母得：1+3x﹣6＝x﹣1，
解得：x＝2，
检验：当x＝2时，x﹣2＝0，
则x＝2是分式方程的增根，
故原方程无解．
【点评】本题考查解分式方程，熟练掌握解方程的方法是解题的关键．
19．（5分）先化简，再从﹣1，1，﹣2三个数字中选择一个你喜欢的数代入上式求值．
【答案】；．
【分析】把括号内式子进行通分，再将除法运算转化成乘法运算，然后进行因式分解、约分得到最简结果，最后根据分式有意义的条件确定a的值，代入计算即可．
【解答】解：原式＝×
＝．
当a＝﹣2时，原式＝＝．
【点评】本题考查分式的化简求值，熟练掌握运算法则是解答本题的关键．
20．（6分）如图，在正方形网格上有一个△ABC，网格上的每个小正方形的边长为1．（无刻度直尺作图）．
（1）在图1中画△ABC关于直线MN的对称图形△A′B′C′，△ABC的面积为 ；
（2）在图2中直线MN上画点Q，使∠QBC＝∠BAC．
【答案】（1）画图见解答；．
（2）见解答．
【分析】（1）根据轴对称的性质作图即可；利用割补法求三角形的面积即可．
（2）由图可得∠ABC＝90°，过点B作AC的垂线，交直线MN于点Q，则点Q即为所求．
【解答】解：（1）如图1，△A′B′C′即为所求．
△ABC的面积为＝＝．
故答案为：．
（2）如图2，由图可得，AB⊥BC，
过点B作AC的垂线，交AC于点P，交直线MN于点Q，
∵∠BCA+∠BAC＝90°，∠BCP+∠CBP＝90°，
∴∠BAC＝∠CBP，
即∠QBC＝∠BAC，
则点Q即为所求．
【点评】本题考查作图﹣轴对称变换，熟练掌握轴对称的性质是解答本题的关键．
21．（6分）观察以下等式：
第1个等式：，
第2个等式：，
第3个等式：，
第4个等式：，
第5个等式：，
……
按照以上规律．解决下列问题：
（1）写出第6个等式： ；
（2）写出你猜想的第n个等式（用含n的式子表示），并证明．
【答案】（1）；
（2）＝1，见解答过程．
【分析】（1）根据所给的等式的形式进行解答即可；
（2）分析所给的等式的形式，再进行总结，对等式左边的式子进行整理即可求证．
【解答】解：（1）第6个等式为：．
故答案为：；
（2）猜想：第n个等式为：＝1，
证明：等式左边＝
＝
＝
＝
＝1
＝右边，
故猜想成立．
【点评】本题主要考查数字的变化规律，解答的关键是分析清楚所给的等式中序号与相应的数之间的关系．
22．（6分）如图，在△ABC中，AB＝AC，点D在BC上，DE⊥AB，DF⊥AC，垂足分别为E、F，且DE＝DF．求证：D是BC的中点．
【答案】见试题解答内容
【分析】首先，根据DE⊥AB，DF⊥AC，且DE＝DF，得到AD是∠BAC的角平分线，再根据等腰三角形三线合一的性质证得结论．
【解答】证明：∵DE⊥AB，DF⊥AC，且DE＝DF，
∴AD是∠BAC的角平分线，
∵在△ABC中，AB＝AC，
∴D是BC的中点．
【点评】本题考查了角平分线的性质和等腰三角形三线合一的性质，解题的关键是证得AD是∠BAC的角平分线．
23．（8分）如图，在△ABC中，AB＝5cm，BC＝a cm，AC＝b cm，且，动点P从点C出发沿射线CB以2cm/s的速度运动，设运动时间为t（s）．
（1）判断△ABC的形状并说明理由；
（2）当t＝ 或 时，△ABP是等腰三角形？（请直接写出答案）
【答案】或．
【分析】（1）根据非负数的性质分别求出a、b，再根据勾股定理的逆定理判断；
（2）分PA＝PB，BP′＝BA两种情况，根据勾股定理解答．
【解答】解：（1）△ABC是直角三角形，
理由如下：∵|a﹣4|+＝0，
∴a﹣4＝0，b﹣3＝0，
解得：a＝4，b＝3，
∵AC2+BC2＝32+42＝25，AB2＝52＝25，
∴AC2+BC2＝AB2，
∴△ABC是直角三角形；
（2）如图，作线段AB的垂直平分线，交BC于P，则PA＝PB，此时△ABP是等腰三角形，
在Rt△ACP中，AC2+PC2＝AP2，即32+PC2＝（4﹣PC）2，
解得：PC＝，
则t＝，
如图，当BP′＝BA＝5时，P′C＝9，
则t＝，
综上所述：当t＝或时，△ABP是等腰三角形，
故答案为：或．
【点评】本题考查的是勾股定理的逆定理、勾股定理、等腰三角形的性质，掌握相关的定理是解题的关键．
24．（8分）根据市场需求，某小型企业为加快生产速度，需要更新生产设备，更新设备后生产效率比更新前提高了25%，设更新设备前每天生产x件产品．解答下列问题：
（1）更新设备后每天生产 1.25x 件产品（用含x的式子表示）；
（2）更新设备前生产2500件产品比更新设备后生产3000件产品多用1天，求更新设备后每天生产多少件产品．
【答案】（1）1.25x；（2）更新设备后每天生产125件产品．
【分析】（1）根据题意和题目中的数据，可以用含x的代数式表示出更新设备后每天生产的产品数；
（2）根据题意和题目中的数据，可以列出相应的分式方程，然后求解即可．
【解答】解：（1）由题意可得，
更新设备后每天生产产品为：x（1+25%）＝1.25x（件），
故答案为：1.25x；
（2）由题意可得，
﹣1＝，
解得x＝100，
经检验，x＝100是原分式方程的解，
∴1.25x＝125，
答：更新设备后每天生产125件产品．
【点评】本题考查分式方程的应用、列代数式，解答本题的关键是明确题意，列出相应的代数式和列出相应的分式方程，注意分式方程要检验．
25．（10分）勾股定理具有丰富的文化内涵，它揭示了直角三角形的三边关系，搭建起几何与代数之间的桥梁，为解决几何问题拓宽了思路．请完成下面问题：
（1）如图1，请你用两种不同方法表示梯形ABCD的面积，从而验证勾股定理．
（2）如图2，在直线l的同侧有两个点C、D，已知点C和点D到直线l的距离分别为2和5，且，现要在直线l上取点P，使得PD+PC的值最小．
①请用无刻度直尺和圆规在图2中确定点P的位置（要求：尺规作图，保留作图痕迹，不写作法）
②直接写出PC+PD的最小值为 ；
（3）借助上面的思考过程，直接写出的最小值为 ．
【答案】（1）见解析；
（2）①见解析；
②；
（3）．
【分析】（1）由梯形，三角形面积公式即可证明问题；
（2）①根据轴对称的性质，作D关于直线l的对称点D′，连接CD′与直线l交于点P；
②根据勾股定理求出CM，根据矩形的性质分别求出CH，D′H，根据勾股定理求出CD′，得到PC+PD，结合题意计算即可；
（3）作A关于直线l的对称点A′，连接CA′与直线l交于点P，则PA+PC的最小值为CA′，然后根据勾股定理即可得到结论．
【解答】（1）证明：由题意得第一种方法：S梯形ABCD＝S△ADE+S△BCE+S△CDE＝ab+c2+ab＝ab+c2，
第二种方法：S梯形ABCD＝（AD+BC）（AE+BE）
＝（a+b）（a+b）
＝（a+b）2，
∴（a+b）2＝ab+c2，
∴a2+2ab+b2＝2ab+c2，
∴a2+b2＝c2；
（2）解：①作D关于直线l的对称点D′，连接CD′与直线l交于点P，点P就是所求的位置．
②PD+PC的最小值为CD′，
作CH⊥l，D′H⊥CH，相交于点H，
作CM⊥D′D于点M，连接CD，
则四边形MD′HC为矩形，
∴D′H＝MC，D′M＝CH＝7，
在Rt△CDM中，CD＝，DM＝5﹣2＝3，
∴CM＝＝8，
在Rt△CD′H中，CH＝7，D′H＝CM＝8，
∴CD′＝＝，
∴PD+PC的最小值为，
故答案为：；
（3）解：如图AB⊥BD于B，CD⊥BD于D，AB＝3，CD＝1，BD＝x，则PD＝5﹣x，
作A关于直线l的对称点A′，连接CA′与直线l交于点P，则PA+PC的最小值为CA′，
根据勾股定理得CA′＝＝．
根据勾股定理得PA+PC＝+，
∴+的最小值为．
【点评】本题是四边形的综合题，考查了勾股定理轴对称﹣最短路径问题，勾股定理的证明，正确地作出图形是解题的关键．
26．（11分）如图，在长方形ABCD中，∠DAB＝∠B＝∠C＝∠D＝90°，AB＝CD＝10，AD＝BC＝4，AB∥CD，AD∥BC．N是边CD上一点，CN＝2．若M为AB边上一个动点，将四边形BCNM沿MN折叠，点B、C的对应点分别为点B′、C′，若线段MB'与边CD交于点E．
（1）如图1，证明：△EMN为等腰三角形；
（2）如图2，当点M与点A重合时，求线段DE的长；
（3）点M从点A向点B运动的过程中，
①线段DE的最大值为 4 ；
②请直接写出点E运动的路径长为 2﹣3 ．
【答案】（1）证明见解答过程；
（2）DE＝3；
（3）①4；
②2﹣3．
【分析】（1）由折叠的性质得∠BMN＝∠EMN，又AB∥CD，有∠ENM＝∠BMN，故∠EMN＝∠ENM，EM＝EN，知△EMN为等腰三角形；
（2）设DE＝x，在Rt△ADE中，可得42+x2＝（8﹣x）2，即可解得即DE＝3；
（3）①过M作MH⊥DC于H，设EN＝EM＝x，则DE＝CD﹣CN﹣EM＝8﹣x，设AM＝m，在Rt△MHE中，HE2+HM2＝ME2，有（8﹣x﹣m）2+42＝x2，故x＝+，根据线段MB'与边CD相交，即可得x＝+≥2＝4，从而DE最大为4；
②由（2）和（3）①可知，当M从A开始，运动到DE最大时，E的路径长为4﹣3＝1；当B'落在CD上时，E与B'重合，求出DE＝DN﹣EN＝8﹣2，故DE由最大运动到B'落在DC时，E的运动路径为4﹣（8﹣2）＝2﹣4，即可得到答案．
【解答】（1）证明：由折叠的性质得∠BMN＝∠EMN，
∵AB∥CD，
∴∠ENM＝∠BMN，
∴∠EMN＝∠ENM，
∴EM＝EN，
∴△EMN为等腰三角形；
（2）解：设DE＝x，
∵CD＝10，AD＝4，CN＝2，
∴EN＝8﹣x，
由（1）知AE＝EN＝8﹣x，
在Rt△ADE中，AD2+DE2＝AE2，
∴42+x2＝（8﹣x）2，
∴x＝3，即DE＝3；
（3）解：①过M作MH⊥DC于H，如图：
设EN＝EM＝x，则DE＝CD﹣CN﹣EM＝8﹣x，
设AM＝m，
∵∠A＝∠D＝∠DHM＝90°，
∴四边形AMHD是矩形，
∴HM＝AD＝4，DH＝AM＝m，
∴HE＝DE﹣DH＝8﹣x﹣m，
在Rt△MHE中，HE2+HM2＝ME2，
∴（8﹣x﹣m）2+42＝x2，
化简整理得x＝+，
∵线段MB'与边CD相交，
∴m＜8，
∴＞0，＞0，
∴x＝+≥2＝4，
∴8﹣x≤4，
∴DE最大为4；
故答案为：4；
②由（2）和（3）①可知，当M从A开始，运动到DE最大时，E的路径长为4﹣3＝1；
当B'落在CD上时，E与B'重合，如图：
此时EC'＝B'C'＝BC＝4，C'N＝CN＝2，∠C'＝∠C＝90°，
∴EN＝＝2，
∴DE＝DN﹣EN＝8﹣2，
∴DE由最大运动到B'落在DC时，E的运动路径为4﹣（8﹣2）＝2﹣4，
∴点M从点A向点B运动的过程中，点E运动的路径长为1+（2﹣4）＝2﹣3．
故答案为：2﹣3．
【点评】本题考查四边形综合应用，涉及矩形中的翻折问题，解题的关键是掌握翻折的性质和矩形的判定与性质．