2024_2025学年新教材高中数学第1章空间向量与立体几何1.1.2空间向量的数量积运算分层作业课件新人教A版选择性必修第一册

这是一份2024_2025学年新教材高中数学第1章空间向量与立体几何1.1.2空间向量的数量积运算分层作业课件新人教A版选择性必修第一册，共27页。
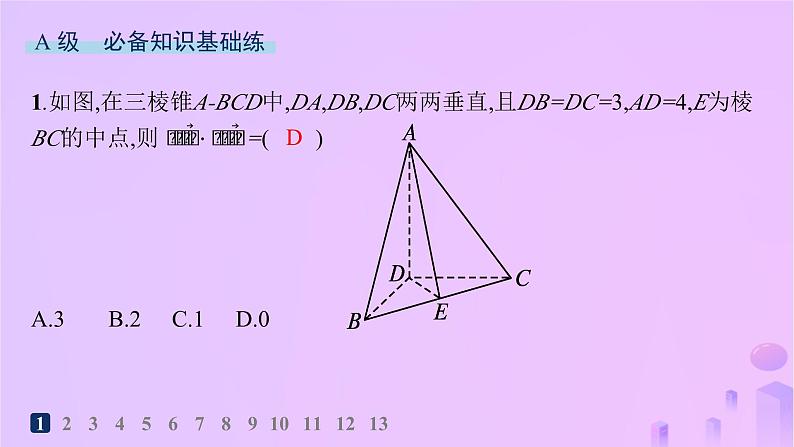
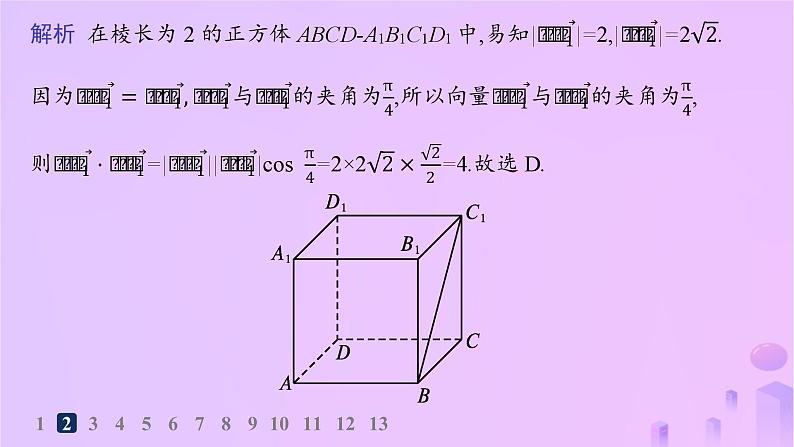
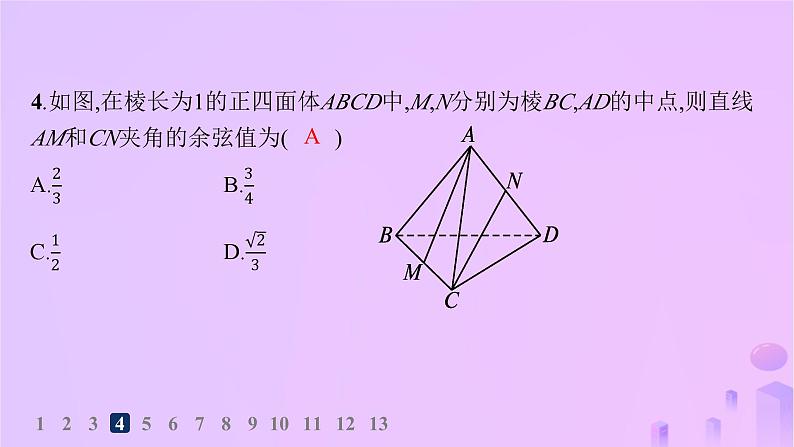
第一章1.1.2　空间向量的数量积运算123456789101112131.如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且DB=DC=3,AD=4,E为棱BC的中点,则 =(　　)A.3 B.2 C.1 D.0D 1234567891011121312345678910111213D 12345678910111213123456789101112133.已知四面体ABCD的所有棱长都等于2,E是棱AB的中点,F是棱CD靠近C的四等分点,则 =(　　)D 12345678910111213123456789101112134.如图,在棱长为1的正四面体ABCD中,M,N分别为棱BC,AD的中点,则直线AM和CN夹角的余弦值为(　　)A12345678910111213123456789101112135.(多选题)已知四面体ABCD中,AB,AC,AD两两互相垂直,则下列结论中,一定成立的是(　　)ABD1234567891011121312345678910111213123456789101112136.(多选题)已知长方体ABCD-A1B1C1D1,则下列向量的数量积可以为0的是(　　)ABC12345678910111213解析 如图所示,若AA1=AD,则AD1⊥B1C,故A正确;若AB=AD,则AC⊥BD.又BB1⊥平面ABCD,则BB1⊥AC.∵BB1∩BD=B,BB1,BD⊂平面B1BDD1,∴AC⊥平面B1BDD1.又BD1⊂平面B1BDD1,∴BD1⊥AC,故B正确;∵AB⊥平面AA1D1D,AD1⊂平面AA1D1D,∴AB⊥AD1,故C正确;∵BD1和BC分别为矩形A1D1CB的对角线和边,∴直线BD1和BC不可能垂直,故D错误.故选ABC.12345678910111213123456789101112138.已知MN是棱长为2的正方体ABCD-A1B1C1D1内切球的一条直径,则2 12345678910111213123456789101112139.在平行四边形ABCD中,AD=4,CD=3,∠D=60°,PA⊥平面ABCD,PA=6,求PC的长.1234567891011121310.(多选题)如图,在平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长都是1,且它们彼此的夹角都是60°,M为A1C1与B1D1的交点.记AC 123456789101112131234567891011121311.如图,在三棱锥P-ABC中,已知PA⊥平面ABC,∠ABC=120°, PA=AB=BC=6,则向量 在向量 上的投影向量为　　　　　(用向量 来表示). 123456789101112131234567891011121312.如图,在正四面体ABCD中,棱长为a,M,N分别是棱AB,CD上的点,且MB=2AM,CN= ND,求MN的长.123456789101112131234567891011121313. 如图,在平行六面体ABCD-A1B1C1D1中,AB=4,AD=2, AA1=2 ,AD1=2 ,∠BAD=60°,∠BAA1=45°,AC与BD相交于点O.(2)求∠DAA1;(3)求OA1的长.1234567891011121312345678910111213