2023-2024学年山东省聊城市冠县七年级(上)期中数学试卷（解析版）

这是一份2023-2024学年山东省聊城市冠县七年级(上)期中数学试卷（解析版），共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（每小题有且只有一个正确答案，每小题3分，满分36分.）
1. 生活中的实物可以抽象出各种各样的几何图形，如图所示的不锈钢漏斗的形状类似于（ ）
A. 圆B. 球C. 圆柱D. 圆锥
【答案】D
【解析】如图所示的不锈钢漏斗的形状类似于圆锥．
故选：D．
2. 已知下列各数：，，0，，，11．其中正数有（ ）
A. 1个B. 2个C. 3个D. 4个
【答案】B
【解析】，11是正数，则正数有2个.
故选：B．
3. 计算，正确的结果是（ ）
A. B. C. D.
【答案】D
【解析】.
故选：D．
4. 某中学七年级进行了一次数学测验，参加人数共400人，为了了解这次数学测验成绩，下列所抽取的样本中较为合理的是（ ）
A. 抽取前100名同学的数学成绩
B. 抽取后100名同学的数学成绩
C. 抽取其中100名女子的数学成绩
D. 抽取各班学号为5的倍数的同学的数学成绩
【答案】D
【解析】要使所抽取的样本较为合理，应尽量使抽样调查能够很好的反映总体的情况，所以抽取各班学号为5号的倍数的同学的数学成绩是较为合理的，它属于简单随机抽样，具有对总体的代表性．
故选：D．
5. 的绝对值是（ ）
A. B. C. D.
【答案】A
【解析】的绝对值为．
故选：A．
6. 如图，数轴上有A、B、C、D四个点，其中表示互为相反数的点是（ ）
A. 点A与点DB. 点A与点C
C. 点B与点CD. 点B与点D
【答案】A
【解析】2与互为相反数.
故选：A．
7. 要清楚地反映一位病人24小时内心跳次数的变化情况，护士要把病人心跳的数据编制成____统计图．要清楚地反映一个家庭中一个月各项支出与总支出之间的关系，应选用____统计图．（ ）
A. 折线；条形B. 折线；扇形
C. 扇形；条形D. 以上都可以
【答案】B
【解析】要清楚地反映一位病人24小时内心跳次数的变化情况，护士要把病人心跳的数据编制成折线统计图．
要清楚地反映一个家庭中一个月各项支出与总支出之间的关系，应选用扇形统计图.
故选：B．
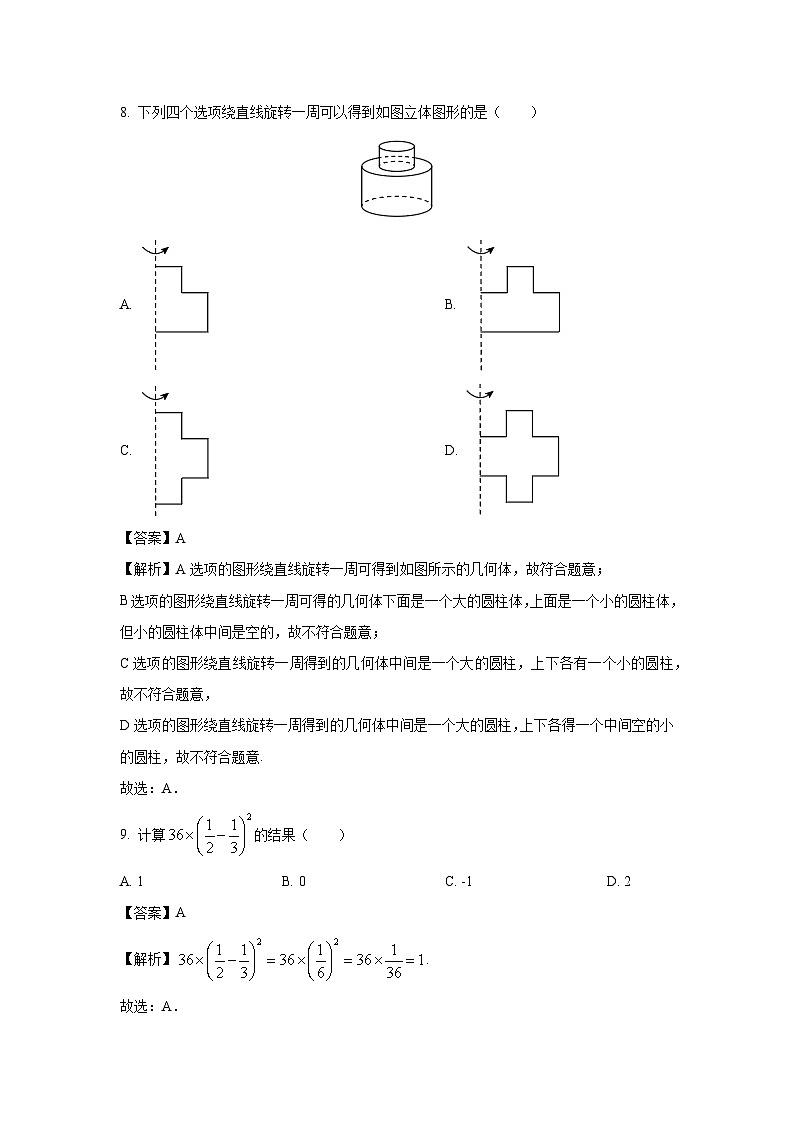
8. 下列四个选项绕直线旋转一周可以得到如图立体图形的是（ ）
A. B.
C. D.
【答案】A
【解析】A选项的图形绕直线旋转一周可得到如图所示的几何体，故符合题意；
B选项的图形绕直线旋转一周可得的几何体下面是一个大的圆柱体，上面是一个小的圆柱体，但小的圆柱体中间是空的，故不符合题意；
C选项的图形绕直线旋转一周得到的几何体中间是一个大的圆柱，上下各有一个小的圆柱，故不符合题意，
D选项的图形绕直线旋转一周得到的几何体中间是一个大的圆柱，上下各得一个中间空的小的圆柱，故不符合题意.
故选：A．
9. 计算的结果（ ）
A. 1B. 0C. -1D. 2
【答案】A
【解析】.
故选：A．
10. 武汉市元月份某一天早晨的气温是-3℃，中午上升了8℃，则中午的气温是（ ）
A. -5℃B. 5℃C. 3℃D. -3℃
【答案】B
【解析】由题意得：中午的气温为.
故选：B．
11. 为了了解2013年昆明市九年级学生学业水平考试的数学成绩，从中随机抽取了1000名学生的数学成绩．下列说法正确的是（ ）
A. 2013年昆明市九年级学生是总体B. 每一名九年级学生是个体
C. 1000名九年级学生是总体的一个样本D. 样本容量是1000
【答案】D
【解析】A、2013年昆明市九年级学生的数学成绩是总体，原说法错误，故本选项不符合题意；
B、每一名九年级学生的数学成绩是个体，原说法错误，故本选项不符合题意；
C、1000名九年级学生的数学成绩是总体的一个样本，原说法错误，故本选项不符合题意；
D、样本容量是1000，该说法正确，故本选项符合题意．
故选：D．
12. 将如图折成一个正方体，点与（ ）会重合．
A. 点B. 点C. 点D. 点
【答案】D
【解析】由正方体表面展开图的特点可知与，重合，与重合，与重合，与重合.
故选：．
二、填空题（共5小题，每小题3分，满分15分.）
13. 有下列一些生活中的现象：
①把原来弯曲的河道改直，河道长度变短；
②将两根细木条叠放在一起，两端恰好重合，如果中间存在缝隙，那么这两根细木条不可能都是直；
③植树时，只要定出两个树坑的位置，就能使同一行的树坑在一条直线上；
④只用两颗钉子就能把一根细木条固定在墙上．
其原理能用基本事实“两点确定一条直线”解释的为______．（只填序号）
【答案】②③④
【解析】①把原来弯曲的河道改直，河道长度变短，其原理能用基本事实“两点之间线段最短”解释，故不符合题意；
②将两根细木条叠放在一起，两端恰好重合，如果中间存在缝隙，那么这两根细木条不可能都是直的，其原理能用基本事实“两点确定一条直线”解释，符合题意；
③植树时，只要定出两个树坑位置，就能使同一行的树坑在一条直线上，其原理能用基本事实“两点确定一条直线”解释，符合题意；
④只用两颗钉子就能把一根细木条固定在墙上，其原理能用基本事实“两点确定一条直线”解释，符合题意．
14. 对我国“天宫空间站梦天实验舱”的零部件检查应采用的调查方式为____．（填“普查”或“抽样调查”）．
【答案】普查．
【解析】“天宫空间站梦天实验舱”的零部件要求高精准，不能出现误差，必须普查．
15. 比较大小：____（填“>”、“<”或“＝”）．
【答案】
【解析】
由＜ ＞.
16. 一次数学测试，如果分为优秀，以分为基准简记，例如分记为分，那么分应记为_______分．
【答案】-9
【解析】86-95=-9．
17. 若，且，则_______．
【答案】0或2
【解析】∵，∴；
∵，∴；
当时，；
当时，．
故的值为0或2．
三、解答题（共8小题，满分69分．要求写出必要的文字说明和解题步骤.）
18. 在下列数中：7，，，0，，，，，，．
负数有：{ …}；
分数有：{ …}．
解：，，
则负数有：{，，，…}，
分数有：{，，，，…}．
19. 如图，C为线段上一点，点B为的中点，且，，求的长．
解：∵点B为的中点，，，，
．
20. 某工厂生产一批精密的零件，要求是（表示圆形工件的直径，单位：），抽查了5个零件，数据如表，超过规定的记作正数，不足的记作负数．
（1）哪些产品是符合要求的？
（2）符合要求的产品中哪个质量最好？用绝对值的知识加以说明
解：（1）根据题意可得零件的直径在和内，
即与标准50的差值应该在之间都是合格的，
所以1号、3号、4号产品是符合要求的.
（2）∵，∴3号产品质量最好．
21. 如图，已知线段，点C在上，点P在外．
（1）根据要求画出图形：画直线，画射线，连接；
（2）写出图中的所有线段．
解：（1）如图，直线，射线，连接.
（2）图中的所有线段为．
22. 计算：
（1）；
（2）；
（3）；
（4）.
解：（1）原式.
（2）原式.
（3）原式
.
（4）原式
．
23. 某商店正在进行商品促销活动（活动规则如右图）．张老师和王老师一起去该商店购物，张老师要买一台800元的洗衣机，促销王老师要买一件200元的羊毛衫．问：这两位老师合着购买比分开购买可以节省多少元钱？
解：分开够买：（元），
合着够买：（元），
（元），
答：这两位老师合着购买比分开购买可以节省100元钱．
24. 为了提高学生的综合素质，某校对七年级学生开设“A烹饪、B种菜、C手工制作、D桌椅维修”四门校本课程，学生必须从四门校本课程中选修一门且只选一门．为了解学生对校本课程的选择意向，学校随机抽取了部分学生进行调查，并将调查情况绘制成如图所示的扇形统计图和条形统计图（均不完整）
请根据图中信息，解答下列问题：
（1）本次调查的学生人数是 人；
（2）将条形统计图补充完整；
（3）计算扇形统计图中“D桌椅维修”所对应的圆心角度数为 °；
（4）已知该校七年级共有600名学生，请估计选择“A烹任”的学生有多少人？
解：（1）本次调查的学生人数是（人）.
（2）调查的学生中选择B的学生数为（人），
条形统计图补充完整如下：
（3）“D桌椅维修”所对应的圆心角度数为.
（4）（人），
答：估计选择“A烹任”的学生有120人．
25. 已知a，b，c均是非零有理数，请完成下面的探索：
（1）试求的值；
（2）试求的值；
（3）请直接写出的值．
解：（1）当a为正数时，；
当a为负数时，.
（2）当，时，；
当，时，；
当，时，；
当，时，.
（3）当，，时，原式；
当，，时，原式；
当，，时，原式；
当，，时，原式；
当，，时，原式；
当，，时，原式；
当，，时，原式；
当，，时，原式，
∴的值为，1，3，．1号
2号
3号
4号
5号