安徽省全椒县2024-2025学年上学期期中考试九年级数学试卷

这是一份安徽省全椒县2024-2025学年上学期期中考试九年级数学试卷，共9页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。
1.若线段，则（ ）
A.B.5C.D.2
2.下列各式中，一定是x的反比例函数的是（ ）
A.B.C.D.
3.已知线段，如果线段是线段和的比例中项，那么线段的长度是（ ）
A.B.8C.9D.10
4.把抛物线向左平移2个单位长度，向下平移4个单位长度后的解析式为（ ）
A.B.C.D.
5.若反比例函数的图象经过点，则的值是（ ）
A.3B.2C.-1D.-3
6.如图，乐器上的一根弦，两个端点A，B固定在乐器板面上，支撑点是靠近点的黄金分割点，支撑点是靠近点的黄金分割点，则C，D之间的距离为（ ）
A.B.C.D.
7.如图，在Rt中，轴，点是AB的中点，点C、D在的图象上，则的值为（ ）
A.-2B.-4C.-6D.-8
8.已知抛物线的顶点坐标为，若，则抛物线与坐标轴的交点个数为（ ）
A.3B.2C.1D.0
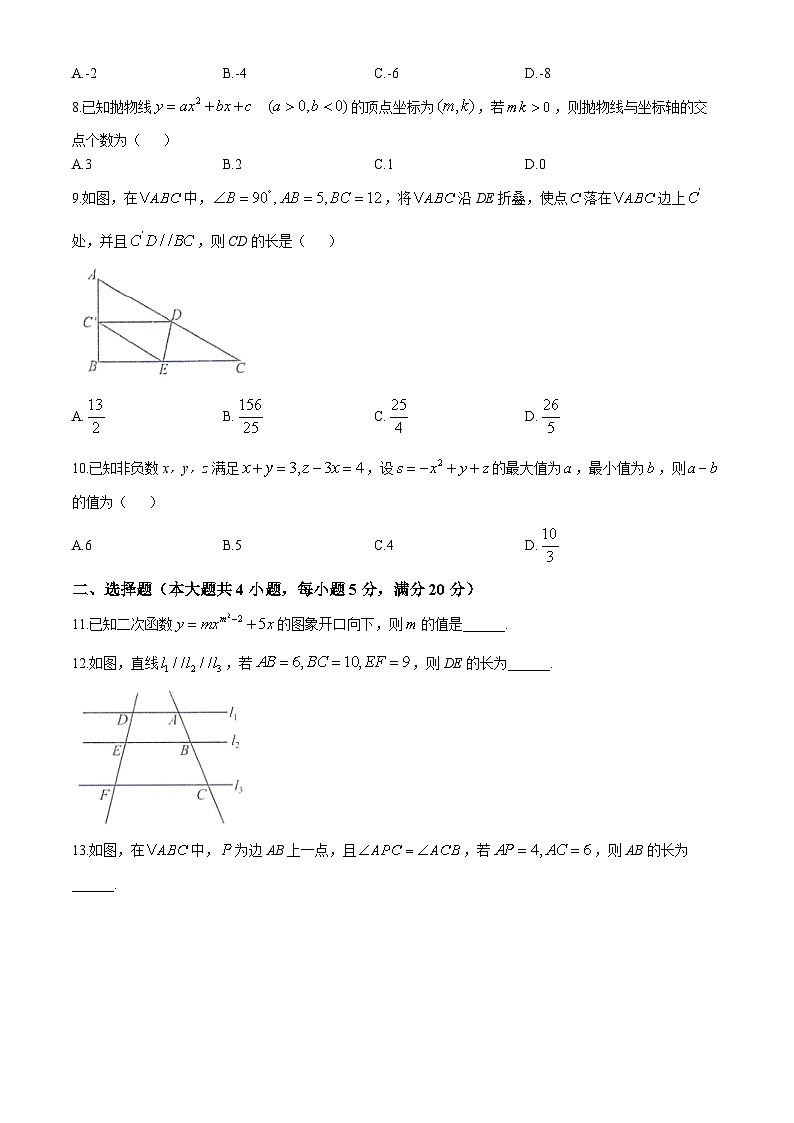
9.如图，在中，，将沿DE折叠，使点落在边上处，并且，则CD的长是（ ）
A.B.C.D.
10.已知非负数x，y，z满足，设的最大值为，最小值为，则的值为（ ）
A.6B.5C.4D.
二、选择题（本大题共4小题，每小题5分，满分20分）
11.已知二次函数的图象开口向下，则的值是______.
12.如图，直线，若，则DE的长为______.
13.如图，在中，为边AB上一点，且，若，则AB的长为______.
14.已知点是抛物线上一动点
（1）当点到轴的距离不大于1时，的取值范围是______；
（2）当点到直线的距离不大于时，的取值范围是，则的值为______.
三、解答题（本大题共9小题，满分90分）
15.（8分）已知，求
（1）
（2）值.
16.（8分）如图，在边长为1个单位长度的小正方形组成的网格中，给出格点及点.
（1）以点O为位似中心，在网格范围内画出，使得与位似，且相似比为2．
（2）填空：______.
17.（8分）已知二次函数.
（1）用配方法把该函数化为（其中a、h、k都是常数且）的形式，并指出函数图象的对称轴和顶点坐标；
（2）求函数图象与轴的交点坐标.
18.（8分）已知在平面直角坐标系xOy中，一次函数的图象与反比例函数的图象相交于点.
（1）求反比例函数的表达式.
（2）若点也在反比例函数的图象上，当时，求的取值范围.
19.（10分）全椒被誉为“中国碧根果之都”，现有一个碧根果销售点在经销时发现：如果每盒碧根果盈利10元，每天可售出50盒；若每盒碧根果涨价1元，日销售量将减少2盒．
（1）现该销售点每天盈利600元，同时又要顾客得到实惠，那么每盒碧根果应涨价多少元？
（2）若该销售点只从经济角度考虑，每盒碧根果应涨价多少元才能每天盈利最高？
20.（10分）已知：如图，在中，的平分线相交于点，过点的直线，分别交AB、AC于点D、E.
（1）求证：；
（2）若，求BC的值.
21.（12分）如图，有长为24m的篱笆，现一面利用墙（墙的最大可用长度为10m）围成中间隔有一道篱笆的长方形花圃，设花圃的宽AB为xm，面积为．
（1）求与的函数关系式及值的取值范围；
（2）要围成面积为的花圃，AB的长是多少米？
22.（12分）已知：如图，在中，AD是BC边上的高.在这个三角形内有一个内接矩形PQMN，矩形的一边在BC上，另两个顶点分别在AB，AC上.
（1）若当时，求PQ的长；
（2）若当矩形PQMN的面积最大时，求这个矩形的边长.
23.（14分）如图，已知抛物线与轴交于点（），且关于直线对称．
（1）求抛物线的解析式；
（2）设此抛物线与直线相交于P，Q两点，平行于轴的直线交PQ于点，交抛物线于点．
①当点在点上方的时候，求MN的表达式（用含的代数式表示）；
②在①的条件下当的面积最大的时候，求的值及面积的最大值．
20242025学年度第一学期期中考试九年级数学学科答案
一、选择题：
1-5、BACAD6-10、BDCBC
二、填空：
11、-212、5.413、914、或5
三、解答题：
15、解：，
，……………………4分
.……………………8分
16、（1）
……………………4分
（2）4:1……………………8分
17、（1）,
对称轴为：，顶点坐标：；……………………4分
（2）当时，有，
图象与轴的交点坐标为：与.……………………8分
18、解：（1）将点代入，
得，
将点的坐标代入得……………………4分
（2），
当时，；当时，
在每个象限内，随的增大而增大，
当时，求的取值范围是.……………………8分
19、（1）解：设每盒碧根果应涨价元，则每天可以销售（50-2x）盒，每箱的利润元，
由题意：……………………2分
整理得，
解得或，……………………4分
Q要顾客得到实惠，．即每盒碧根果应涨价5元．……………………5分
（2）解：设利润为元，则
整理得，……………………8分
，且，
当每盒碧根果应涨价7.5元获利最高……………………10分
20、（1）证明：在VABC中，OB和OC分别平分和，
，
又，
，
，
，
；……………………5分
（2），
，
，即.……………………10分
21、（1）
又，；……………………6分
（2）根据题意，，
解得：，
又.……………………12分
22.（1）四边形PQMN是矩形，，
又，
四边形PEDN是矩形，，由知，
，即，解得；……………………6分
（2）设，则，
，即，
矩形PQMN的面积
，
当时，矩形PQMN的面积取得最大值600，
此时.
所以，这个矩形的边长分别为30，20……………………分
23、解（1）由题意得：，解得，
故抛物线的表达式为；……………………4分
（2）联立PQ表达式和二次函数表达式得，解得或，
故点P、Q的坐标分别为，……………………6分
①设点的坐标为，则点的坐标为，
点在点上方，
……………………10分
②
，故的面积有最大值，
当时，的面积最大值为.……………………14分