2025年中考数学一轮复习讲与练第1章第2讲 整式及因式分解（题型突破+专题精练）（2份，原卷版+解析版）

这是一份2025年中考数学一轮复习讲与练第1章第2讲 整式及因式分解（题型突破+专题精练）（2份，原卷版+解析版），文件包含2025年中考数学一轮复习讲与练第1章第2讲整式及因式分解题型突破+专题精练原卷版docx、2025年中考数学一轮复习讲与练第1章第2讲整式及因式分解题型突破+专题精练解析版docx等2份试卷配套教学资源，其中试卷共53页， 欢迎下载使用。
1．（2018·河北定兴·中考模拟）若x﹣=3，则=（ ）
A．11B．7C．D．
【答案】C
【分析】先由x﹣=3两边同时平方变形为，进而变形为，从而得解．
【解析】解：∵x﹣=3，∴，∴，
∴，∴，故选：C．
【点睛】此题要运用完全平方公式进行变形.根据a2+b2=(a+b)2-2ab把原式变为，再通分，最后再取倒数.易错点是忘记加上两数积的2倍．
2．（2021·湖北十堰市·中考真题）已知，则_________．
【答案】36
【分析】
先把多项式因式分解，再代入求值，即可．
【详解】
∵，
∴原式=，
故答案是：36．
【点睛】
本题主要考查代数式求值，掌握提取公因式法和公式法分解因式，是解题的关键．
3．（2020·内蒙古包头·初三二模）若m﹣＝3，则m2+＝_____．
【答案】11
【分析】根据完全平方公式，把已知式子变形，然后整体代入求值计算即可得出答案．
【解析】解：∵＝m2﹣2+＝9，∴m2+＝11，故答案为11．
【点睛】此题主要考查完全平方公式的应用，解题的关键是熟知完全平方公式的变形.
4．（2019·四川新都·中考模拟）已知（2019﹣a）2+（a﹣2017）2＝7，则代数式（2019﹣a）（a﹣2017）的值是_____．
【答案】
【分析】根据完全平方公式的变式：ab= 利用整体代入的思想求解即可.
【解析】解：∵（2019﹣a）2+（a﹣2017）2＝7，
∴（2019﹣a）（a﹣2017）＝{[（2019﹣a）+（a﹣2017）]2﹣[（2019﹣a）2+（a﹣2017）2]}＝，
故答案为：.
【点睛】本题考查了完全平方公式的应用，熟练掌握公式的变式是解题关键.
5.（2022·四川乐山）已知，则______．
【答案】
【分析】根据已知式子，凑完全平方公式，根据非负数之和为0，分别求得的值，进而代入代数式即可求解．
【详解】解：，
，
即，
，
，
故答案为：．
【点睛】本题考查了因式分解的应用，掌握完全平方公式是解题的关键．
6．（2022·湖南邵阳）已知，则_________．
【答案】2
【分析】将变形为即可计算出答案．
【详解】
∵
∴
故答案为：2．
【点睛】本题考查代数式的性质，解题的关键是熟练掌握代数式的相关知识．
7．（2022·山东滨州）若，，则的值为_______．
【答案】90
【分析】将变形得到，再把，代入进行计算求解．
【详解】解：∵，，
∴ ．故答案为：90．
【点睛】本题主要考查了代数式求值，完全平方公式的应用，灵活运用完全平方公式是解答关键．
8．（2020·北京中考真题）已知，求代数式的值．
【答案】，-2
【分析】先按照整式的混合运算化简代数式，注意利用平方差公式进行简便运算，再把变形后，整体代入求值即可．
【解析】解：原式=
∵，∴，∴，∴原式=．
【点睛】本题考查的是整式化简求值，掌握利用平方差公式进行简便运算，整体代入求值是解题的关键．
9．（2019·黑龙江中考真题）已知：ab=1，b=2a-1，求代数式的值．
【答案】-1.
【分析】根据ab=1，b=2a-1，可以求得b-2a的值，从而可以求得所求式子的值．
【解析】∵ab=1，b=2a-1，∴b-2a=-1，∴
【点睛】本题考查分式的化简求值，解答本题的关键是明确分式化简求值的方法．
10．（2021·四川凉山彝族自治州·中考真题）已知，求的值．
【答案】-4
【分析】
根据已知求出xy=-2，再将所求式子变形为，代入计算即可．
【详解】
解：∵，
∴，
∴，
∴．
【点睛】
本题考查了代数式求值，解题的关键是掌握分式的运算法则和因式分解的应用．
11．（2022·江苏苏州）已知，求的值．
【答案】，3
【分析】先将代数式化简，根据可得，整体代入即可求解．
【详解】原式．
∵，
∴．
∴原式．
【点睛】本题考查了整式的乘法运算，代数式化简求值，整体代入是解题的关键．
12．（2023·山东·统考中考真题）已知实数满足，则_________．
【答案】8
【分析】由题意易得，然后整体代入求值即可．
【详解】解：∵，
∴，
∴
；
故答案为8．
【点睛】本题主要考查因式分解及整体思想，熟练掌握利用整体思维及因式分解求解整式的值．
题型二整式及其相关概念
13．（2023·甘肃武威·统考中考真题）计算：（ ）
A．2B．C．D．
【答案】B
【分析】先计算单项式乘以多项式，再合并同类项即可．
【详解】解：，
故选：B.
【点睛】此题考查了整式的四则混合运算，熟练掌握单项式乘以多项式的运算法则是解题的关键．
14．（湖北荆州·中考真题）下列代数式中，整式为（ ）
A．x+1B．C．D．
【答案】A
【解析】
【分析】直接利用整式、分式、二次根式的定义分析得出答案．
【详解】A、x+1是整式，故此选项正确；B、是分式，故此选项错误；
C、是二次根式，故此选项错误；D、是分式，故此选项错误，故选A．
【点睛】本题考查了整式、分式、二次根式的定义，熟练掌握相关定义是解题关键．
15．（山东济宁·中考真题）如果整式是关于x的三次三项式，那么n等于
A．3B．4C．5D．6
【答案】C
【解析】根据多项式次数的定义得到n－2=3，解得：n=5．故选C．
16．（2022·湖南湘潭）下列整式与为同类项的是（ ）
A．B．C．D．
【答案】B
【解析】【分析】根据同类项的定义：所含字母相同，并且相同字母的指数也相同，这样的项叫做同类项，结合选项求解．
【详解】解：由同类项的定义可知，a的指数是1，b的指数是2．
A、a的指数是2，b的指数是1，与不是同类项,故选项不符合题意；
B、a的指数是1，b的指数是2，与是同类项,故选项符合题意；
C、a的指数是1，b的指数是1，与不是同类项,故选项不符合题意；
D、a的指数是1，b的指数是2，c的指数是1，与不是同类项,故选项不符合题意．故选：B．
【点睛】此题考查了同类项，判断同类项只要两看，即一看所含有的字母是否相同，二看相同字母的指数是否相同．
17．（2020·广西河池·中考模拟）下列单项式中，与3a2b为同类项的是（ ）
A． B．C．3abD．3
【答案】A
【分析】单项式3a2b含有字母a、b，且次数分别为2、1，根据同类项的定义进行判断．
【解析】解：∵3a2b含有字母a、b，且次数分别为2、1，∴与3a2b是同类项的是﹣a2b．故选：A．
【点睛】本题考查了同类项的定义，解题的关键是熟知同类项的定义．
18.（2020·四川泸州·中考真题）若与是同类项，则a的值是___________．
【答案】5
【分析】根据同类项的定义（所含字母相同，相同字母的指数相同）列出方程，求出a的值．
【解析】解：∵与是同类项，∴a-1=4，∴a=5，故答案为：5.
【点睛】本题考查了同类项的定义，同类项定义中的两个“相同”：相同字母的指数相同，是易混点，因此成了中考的常考点．
题型三规律探索题
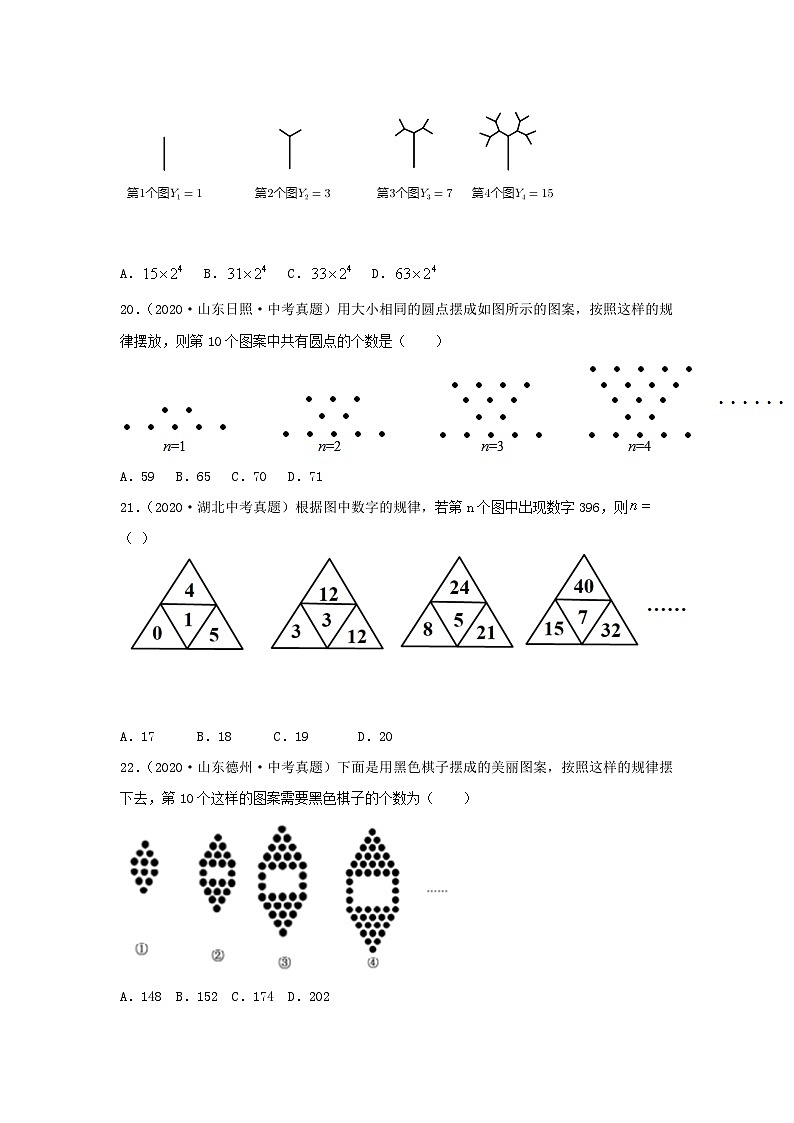
19．（2021·广西玉林市·中考真题）观察下列树枝分杈的规律图，若第个图树枝数用表示，则（ ）
A．B．C．D．
【答案】B
【分析】
根据题目中的图形，可以写出前几幅图中树枝分杈的数量，从而可以发现树枝分杈的变化规律，进而得到规律，代入规律求解即可．
【详解】
解：由图可得到：

则：，
∴，
故答案选：B．
【点睛】
本题考查图形规律，解答本题的关键是明确题意，利用数形结合的思想解答．
20．（2020·山东日照·中考真题）用大小相同的圆点摆成如图所示的图案，按照这样的规律摆放，则第10个图案中共有圆点的个数是（ ）
A．59B．65C．70D．71
【答案】C
【分析】由题意观察图形可知，第1个图形共有圆点5+2个；第2个图形共有圆点5+2+3个；第3个图形共有圆点5+2+3+4个；第4个图形共有圆点5+2+3+4+5个；…；则第n个图形共有圆点5+2+3+4+…+n+（n+1）个；由此代入n=10求得答案即可．
【解析】解：根据图中圆点排列，当n＝1时，圆点个数5+2；当n＝2时，圆点个数5+2+3；
当n＝3时，圆点个数5+2+3+4；当n＝4时，圆点个数5+2+3+4+5，…
∴当n＝10时，圆点个数5+2+3+4+5+6+7+8+9+10+11＝4+（1+2+3+4+5+6+7+8+9+10+11）
＝．故选：C．
【点睛】本题考查图形的变化规律，注意找出数量上的变化规律，从而推出一般性的结论，利用规律解决问题．
21．（2020·湖北中考真题）根据图中数字的规律，若第n个图中出现数字396，则（ ）
A．17 B．18 C．19 D．20
【答案】B
【分析】观察上三角形，下左三角形，下中三角形，下右三角形各自的规律，让其等于396，解得为正整数即成立，否则舍去．
【解析】根据图形规律可得：
上三角形的数据的规律为：，若，解得不为正整数，舍去；
下左三角形的数据的规律为：，若，解得不为正整数，舍去；
下中三角形的数据的规律为：，若，解得不为正整数，舍去；
下右三角形的数据的规律为：，若，解得，或，舍去。故选：B．
【点睛】本题考查了有关数字的规律，能准确观察到相关规律是解题的关键．
22．（2020·山东德州·中考真题）下面是用黑色棋子摆成的美丽图案，按照这样的规律摆下去，第10个这样的图案需要黑色棋子的个数为（ ）

A．148B．152C．174D．202
【答案】C
【分析】观察各图可知，第一个图案需要黑色棋子的个数为(1+2+3)×2（个），第二个图案需要的个数为[(1+2+3+4)×2+2×1]（个），第三个图案需要的个数为[(1+2+3+4+5)×2+2×2]（个），第四个图案需要的个数为[(1+2+3+4+5+6)×2+2×3]（个）…由此可以推出第n个图案需要的个数为（个），所以第10个图案需要的个数只需将n=10代入即可．
【解析】解：由图知第一个图案需要黑色棋子的个数为(1+2+3)×2（个）；
第二个图案需要的个数为[(1+2+3+4)×2+2×1]（个）；
第三个图案需要的个数为[(1+2+3+4+5)×2+2×2]（个）；
第四个图案需要的个数为[(1+2+3+4+5+6)×2+2×3]（个）；…
第n个图案需要的个数为（个）
∴第10个图案需要的个数为[(1+2+3+4+5+6+7+8+9+10+11+12)×2+2×9=174（个）故选C．
【点睛】本题考查了图形的变化．解题的关键是观察各个图形找到它们之间的规律．
23．（2020·湖南娄底·中考真题）下列各正方形中的四个数之间都有相同的规律，根据此规律，x的值为（ ）
A．135B．153C．170D．189
【答案】C
【分析】由观察发现每个正方形内有：可求解，从而得到，再利用之间的关系求解即可．
【解析】解：由观察分析：每个正方形内有：
由观察发现：
又每个正方形内有：
故选C．
【点睛】本题考查的是数字类的规律题，掌握由观察，发现，总结，再利用规律是解题的关键．
24．（2022·山东泰安）观察下列图形规律，当图形中的“○”的个数和“．”个数差为2022时，n的值为____________．
【答案】不存在
【分析】首先根据n=1、2、3、4时，“•”的个数分别是3、6、9、12，判断出第n个图形中“•”的个数是3n；然后根据n=1、2、3、4，“○”的个数分别是1、3、6、10，判断出第n个“○”的个数是；最后根据图形中的“○”的个数和“．”个数差为2022，列出方程，解方程即可求出n的值是多少即可．
【详解】解：∵n=1时，“•”的个数是3=3×1；
n=2时，“•”的个数是6=3×2；
n=3时，“•”的个数是9=3×3；
n=4时，“•”的个数是12=3×4；
……
∴第n个图形中“•”的个数是3n；
又∵n=1时，“○”的个数是1=；
n=2时，“○”的个数是，
n=3时，“○”的个数是，
n=4时，“○”的个数是，
……
∴第n个“○”的个数是，
由图形中的“○”的个数和“．”个数差为2022
①，②
解①得：无解
解②得：
故答案为：不存在
【点睛】本题考查了图形类规律，解一元二次方程，找到规律是解题的关键．
25．（2022·四川遂宁）“勾股树”是以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程所画出来的图形，因为重复数次后的形状好似一棵树而得名．假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树，按照勾股树的作图原理作图，则第六代勾股树中正方形的个数为______．
【答案】127
【分析】由已知图形观察规律，即可得到第六代勾股树中正方形的个数．
【详解】解：∵第一代勾股树中正方形有1+2=3（个），
第二代勾股树中正方形有1+2+22=7（个），
第三代勾股树中正方形有1+2+22+23=15（个），．
∴第六代勾股树中正方形有1+2+22+23+24+25+26=127（个），
故答案为：127．
【点睛】本题考查图形中的规律问题，解题的关键是仔细观察图形，得到图形变化的规律．
26．（2022·江西）将字母“C”，“H”按照如图所示的规律摆放，依次下去，则第4个图形中字母“H”的个数是（ ）
A．9B．10C．11D．12
【答案】B
【分析】列举每个图形中H的个数，找到规律即可得出答案．
【详解】解：第1个图中H的个数为4，
第2个图中H的个数为4+2，
第3个图中H的个数为4+2×2，
第4个图中H的个数为4+2×3=10，故选：B．
【点睛】本题考查了规律型：图形的变化类，通过列举每个图形中H的个数，找到规律：每个图形比上一个图形多2个H是解题的关键．
27．（2022·云南）按一定规律排列的单项式：x，3x²，5x³，7x，9x，……，第n个单项式是（ ）
A．(2n-1)B．(2n+1)C．(n-1)D．(n+1)
【答案】A
【分析】系数的绝对值均为奇数，可用(2n-1)表示；字母和字母的指数可用xn表示．
【详解】解：依题意，得第n项为（2n-1）xn，故选：A．
【点睛】本题考查的是单项式，根据题意找出规律是解答此题的关键．
28．（2022·重庆）把菱形按照如图所示的规律拼图案，其中第①个图案中有1个菱形，第②个图案中有3个菱形，第③个图案中有5个菱形，…，按此规律排列下去，则第⑥个图案中菱形的个数为（ ）
A．15B．13C．11D．9
【答案】C
【分析】根据第①个图案中菱形的个数：；第②个图案中菱形的个数：；第③个图案中菱形的个数：；…第n个图案中菱形的个数：，算出第⑥个图案中菱形个数即可．
【详解】解：∵第①个图案中菱形的个数：；
第②个图案中菱形的个数：；
第③个图案中菱形的个数：；…
第n个图案中菱形的个数：，
∴则第⑥个图案中菱形的个数为：，故C正确．故选：C．
【点睛】本题主要考查的是图案的变化，解题的关键是根据已知图案归纳出图案个数的变化规律．
29．（2020·湖南中考真题）如图，将一枚跳棋放在七边形ABCDEFG的顶点A处，按顺时针方向移动这枚跳棋2020次．移动规则是：第k次移动k个顶点（如第一次移动1个顶点，跳棋停留在B处，第二次移动2个顶点，跳棋停留在D处），按这样的规则，在这2020次移动中，跳棋不可能停留的顶点是（ ）
A．C、EB．E、FC．G、C、ED．E、C、F
【答案】D
【分析】设顶点A，B，C，D，E，F，G分别是第0，1，2，3，4，5，6格，因棋子移动了k次后走过的总格数是1+2+3+…+k＝k（k+1），然后根据题目中所给的第k次依次移动k个顶点的规则，可得到不等式最后求得解．
【解析】设顶点A，B，C，D，E，F，G分别是第0，1，2，3，4，5，6格，
因棋子移动了k次后走过的总格数是1+2+3+…+k＝k（k+1），应停在第k（k+1）﹣7p格，
这时P是整数，且使0≤k（k+1）﹣7p≤6，分别取k＝1，2，3，4，5，6，7时，
k（k+1）﹣7p＝1，3，6，3，1，0，0，发现第2，4，5格没有停棋，若7＜k≤2020，
设k＝7+t（t＝1，2，3）代入可得，k（k+1）﹣7p＝7m+t（t+1），
由此可知，停棋的情形与k＝t时相同，故第2，4，5格没有停棋，即顶点C，E和F棋子不可能停到．
故选：D．
【点睛】本题考查的是探索图形、数字变化规律，从图形中提取信息，转化为数字信息，探索数字变化规律是解答的关键.
30．（2022·重庆）用正方形按如图所示的规律拼图案，其中第①个图案中有5个正方形，第②个图案中有9个正方形，第③个图案中有13个正方形，第④个图案中有17个正方形，此规律排列下去，则第⑨个图案中正方形的个数为（ ）
A．32B．34C．37D．41
【答案】C
【分析】第1个图中有5个正方形，第2个图中有9个正方形，第3个图中有13个正方形，……，由此可得：每增加1个图形，就会增加4个正方形，由此找到规律，列出第n个图形的算式，然后再解答即可．
【详解】解：第1个图中有5个正方形；
第2个图中有9个正方形，可以写成：5+4=5+4×1；
第3个图中有13个正方形，可以写成：5+4+4=5+4×2；
第4个图中有17个正方形，可以写成：5+4+4+4=5+4×3；．．．
第n个图中有正方形，可以写成：5+4（n-1）=4n+1；
当n=9时，代入4n+1得：4×9+1=37．故选：C．
【点睛】本题主要考查了图形的变化规律以及数字规律，通过归纳与总结结合图形得出数字之间的规律是解决问题的关键．
31．（2020·湖北咸宁·中考真题）按一定规律排列的一列数：3，，，，，，，，…，若a，b，c表示这列数中的连续三个数，猜想a，b，c满足的关系式是__________．
【答案】bc=a
【分析】根据题目中的数字，可以发现相邻的数字之间的关系，从而可以得到a，b，c之间满足的关系式．
【解析】解：∵一列数：3，，，，，，，，…，
可发现：第n个数等于前面两个数的商，
∵a，b，c表示这列数中的连续三个数，∴bc=a，故答案为：bc=a．
【点睛】本题考查数字的变化类，解答本题的关键是明确题意，发现题目中数字的变化规律，求出a，b，c之间的关系式．
32．（山西中考真题）一组按规律排列的式子：则第n个式子是 .
【答案】（n为正整数）
【解析】寻找规律：已知式子可写成：，分母为奇数，可写成2n-1，分子中字母a的指数为偶数2n．∴第n个式子是（n为正整数）．
33．（2022·安徽）观察以下等式：
第1个等式：，
第2个等式：，
第3个等式：，
第4个等式：，……
按照以上规律．解决下列问题：(1)写出第5个等式：________；
(2)写出你猜想的第n个等式（用含n的式子表示），并证明．
【答案】(1)
(2)，证明见解析
【分析】（1）观察第1至第4个等式中相同位置的数的变化规律即可解答；
（2）观察相同位置的数变化规律可以得出第n个等式为，利用完全平方公式和平方差公式对等式左右两边变形即可证明．
(1)解：观察第1至第4个等式中相同位置数的变化规律，可知第5个等式为：，故答案为：；
(2)解：第n个等式为，
证明如下：等式左边：，
等式右边：
，
故等式成立．
【点睛】本题考查整式规律探索，发现所给数据的规律并熟练运用完全平方公式和平方差公式是解题的关键．
题型四幂的运算
34．（2022·江苏宿迁）下列运算正确的是（ ）
A． B． C． D．
【答案】C
【分析】由合并同类项可判断A，由同底数幂的乘法可判断B，由积的乘方运算可判断C，由幂的乘方运算可判断D，从而可得答案．
【详解】解：， 故A不符合题意；
， 故B不符合题意；
， 故C符合题意；
， 故D不符合题意；故选：C
【点睛】本题考查的是合并同类项，同底数幂的乘法，积的乘方运算，幂的乘方运算，掌握以上基础运算是解本题的关键．
35．（2022·湖南株洲）下列运算正确的是（ ）
A． B． C． D．
【答案】A
【分析】根据同底数幂相乘，幂的乘方，积的乘方，分式的化简，逐项判断即可求解．
【详解】解：A、，故本选项正确，符合题意；
B、，故本选项错误，不符合题意；
C、，故本选项错误，不符合题意；
D、，故本选项错误，不符合题意；故选：A
【点睛】本题主要考查了同底数幂相乘，幂的乘方，积的乘方，分式的化简，熟练掌握相关运算法则是解题的关键．
36．（2022·陕西）计算：（ ）
A．B．C．D．
【答案】C
【分析】利用单项式乘单项式的法则进行计算即可．
【详解】解：．故选：C．
【点睛】本题考查了单项式乘单项式的运算，正确地计算能力是解决问题的关键．
37．（2022·浙江嘉兴）计算a2·a（ ）
A．aB．3aC．2a2D．a3
【答案】D
【分析】根据同底数幂的乘法法则进行运算即可．
【详解】解： 故选D
【点睛】本题考查的是同底数幂的乘法，掌握“同底数幂的乘法，底数不变，指数相加”是解本题的关键．
38．（2020·江苏盐城·中考真题）下列运算正确的是：（ ）
A．B．C．D．
【答案】C
【分析】根据整式的加减与幂的运算法则即可判断．
【解析】A.，故错误； B. ，故错误；
C.，正确； D. ，故错误；故选C．
【点睛】此题主要考查整式与幂的运算，解题的关键是熟知其运算法则．
39．（2020·山东济南·中考真题）下列运算正确的是（ ）
A．（﹣2a3）2＝4a6 B．a2•a3＝a6 C．3a+a2＝3a3 D．（a﹣b）2＝a2﹣b2
【答案】A
【分析】根据各个选项中的运算，可以计算出正确的结果，从而可以解答本题．
【解析】解：∵（﹣2a3）2＝4a6，故选项A正确；∵a2•a3＝a5，故选项B错误；
∵3a+a2不能合并，故选项C错误；∵（a﹣b）2＝a2﹣2ab+b2，故选项D错误；故选：A．
【点睛】本题考查的是积的乘方，同底数幂的乘法，合并同类项，完全平方公式，掌握以上知识是解题的关键．
40.（2020·江苏徐州·）下列计算正确的是（ ）
A．B．C．D．
【答案】D
【分析】由合并同类项、同底数幂除法，完全平方公式、积的乘方，分别进行判断，即可得到答案．
【解析】解：A、，故A错误；B、，故B错误；
C、，故C错误；D、，故D正确；故选：D．
【点睛】本题考查了同底数幂除法，积的乘方，完全平方公式，合并同类项，解题的关键是熟练掌握运算法则进行解题．
题型五整式的运算
41．（2022·四川眉山）下列运算中，正确的是（ ）
A．B．
C．D．
【答案】D
【分析】根据同底数幂的乘法法则，合并同类项，完全平方公式，单项式乘多项式的法则分析选项即可知道答案．
【详解】解：A. ，根据同底数幂的乘法法则可知：，故选项计算错误，不符合题意；
B. ，和不是同类项，不能合并，故选项计算错误，不符合题意；
C. ，根据完全平方公式可得：，故选项计算错误，不符合题意；
D. ，根据单项式乘多项式的法则可知选项计算正确，符合题意；
故选：D
【点睛】本题考查同底数幂的乘法法则，合并同类项，完全平方公式，单项式乘多项式的法则，解题的关键是掌握同底数幂的乘法法则，合并同类项，完全平方公式，单项式乘多项式的法则．
42．（2022·江西）下列计算正确的是（ ）
A． B． C． D．
【答案】B
【分析】利用同底数幂的乘法，去括号法则，单项式乘多项式，完全平方公式对各选项依次判断即可．
【详解】解：A、，故此选项不符合题意；
B、，故此选项符合题意；
C、，故此选项不符合题意；
D、，故此选项不符合题意．故选：B．
【点睛】本题考查了整式的混合运算，涉及到同底数幂的乘法，去括号法则，单项式乘多项式的运算法则，完全平方公式等知识．熟练掌握各运算法则和的应用是解题的关键．
43．（2020·江苏连云港·统考二模）分解因式：3a2+6ab+3b2=________________．
【答案】3（a+b）2
【分析】先提取公因式3，再根据完全平方公式进行二次分解．完全平方公式：a2+2ab+b2=（a+b）2．
【详解】3a2+6ab+3b2=3（a2+2ab+b2）=3（a+b）2．
故答案为：3（a+b）2．
【点睛】本题考查了提公因式法，公式法分解因式．提取公因式后利用完全平方公式进行二次分解，注意分解要彻底．
44．（2020·湖北随州）先化简，再求值：，其中，．
【答案】，．
【分析】先根据整式的乘法法则化简整式，再将字母的值代入结果计算求值即可．
【解析】
当时，原式．
【点睛】本题主要考查了整式的混合运算----化简求值，解答本题的关键是明确整式化简求值的方法．
45．（2020·江苏南通·）计算：（2m+3n）2﹣（2m+n）（2m﹣n）；
【答案】12mn+10n2；
【分析】根据完全平方公式，平方差公式进行计算即可；
【解析】解：（1）原式＝4m2+12mn+9n2﹣（4m2﹣n2）＝4m2+12mn+9n2﹣4m2+n2＝12mn+10n2；
【点睛】本题考查了整式的混合运算，熟知完全平方公式，平方差公式，通分，约分，因式分解计算是解题的关键．
46．（2019·浙江宁波·中考真题）先化简，再求值：，其中.
【答案】
【分析】根据平方差公式、单项式乘多项式的法则把原式化简，代入计算即可．
【解析】（x-2）（x+2）-x（x-1）=x2-4-x2+x=x-4，当x=3时，原式=x-4=-1．
【点睛】本题考查的是整式的化简求值，掌握整式的混合运算法则是解题的关键．
47．（2022·湖南衡阳）先化简，再求值：，其中，．
【答案】，
【分析】利用平方差公式与多项式乘法法则进行化简，再代值计算．
【详解】解：原式，
将，代入式中得：
原式．
【点睛】本题考查多项式乘法与平方差公式，熟练掌握相关运算法则是解题的关键．
48．（2022·浙江丽水）先化简，再求值：，其中．
【答案】；2
【分析】先利用平方差公式，单项式与多项式乘法化简，然后代入即可求解．
【详解】
当时，
原式．
【点睛】本题考查了整式的化简求值，正确地把代数式化简是解题的关键．
49.先化简，再求值：，其中．
【答案】；2
【分析】先利用平方差公式，单项式与多项式乘法化简，然后代入即可求解．
【详解】
当时，
原式．
【点睛】本题考查了整式的化简求值，正确地把代数式化简是解题的关键．
50.先化简，再求值：，其中，．
【答案】，
【分析】利用平方差公式与多项式乘法法则进行化简，再代值计算．
【详解】解：原式，
将，代入式中得：
原式．
【点睛】本题考查多项式乘法与平方差公式，熟练掌握相关运算法则是解题的关键．
51.已知，求的值．
【答案】，3
【分析】先将代数式化简，根据可得，整体代入即可求解．
【详解】原式．
∵，
∴．
∴原式．
【点睛】本题考查了整式的乘法运算，代数式化简求值，整体代入是解题的关键．
52.先因式分解，再计算求值：，其中．
【答案】，30
【分析】
先利用提公因式法和平方差公式进行因式分解，再代入x的值即可．
【详解】
解：，
当时，原式．
【点睛】
本题考查因式分解，掌握提公因式法和公式法是解题的关键．
53.先化简，再求值：，其中．
【答案】，7．
【分析】
先计算完全平方公式、平方差公式，再计算整式的加减法，然后将代入求值即可得．
【详解】
解：原式，
，
将代入得：原式．
【点睛】
本题考查了整式的化简求值，熟记完全平方公式和平方差公式是解题关键．
54.先化简，再求值：，其中．
【答案】
【分析】
首先利用平方差公式，单项式乘以多项式去括号，再合并同类项，然后将a的值代入化简后的式子，即可解答本题．
【详解】


当时，
原式=．
【点睛】
本题考查了整式的混合运算，解题的关键是熟练运用整式的运算法则，本题属于基础题型．
55.先化简，再求值：，其中．
【答案】，
【分析】
先根据平方差公式和单项式乘以多项式进行计算，再合并同类项，最后代入求出答案即可．
【详解】
解：
，
当时，原式．
【点睛】
本题考查了平方差公式，单项式乘以多项式，合并同类项，运用平方差公式是解题的关键．
题型六因式分解
56．（2022·湖南怀化）因式分解：_____．
【答案】
【分析】根据提公因式法和平方差公式进行分解即可．
【详解】解：，
故答案为：
【点睛】本题考查了提公因式法和平方差公式，熟练掌握提公因式法和平方差公式是解题的关键．
57．（2022·浙江绍兴）分解因式： ＝ ______．
【答案】
【分析】利用提公因式法即可分解．
【详解】，
故答案为：．
【点睛】本题考查了用提公因式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解．
58．（2022·浙江宁波）分解因式：x2-2x+1=__________．
【答案】（x-1）2
【详解】由完全平方公式可得：
故答案为．
【点睛】错因分析 容易题.失分原因是：①因式分解的方法掌握不熟练；②因式分解不彻底.
59．（2021·广西贺州市·中考真题）多项式因式分解为（ ）
A．B．C．D．
【答案】A
【分析】
先提取公因式，再利用完全平方公式将括号里的式子进行因式分解即可
【详解】
解：
故答案选：A．
【点睛】
本题考查了提公因式法和公式法进行因式分解．正确应用公式分解因式是解题的关键．
60．（2021·江苏宿迁市·中考真题）分解因式：=______．
【答案】a（b+1）（b﹣1）．
【详解】
解：原式==a（b+1）（b﹣1），
故答案为a（b+1）（b﹣1）．
61．（2021·浙江丽水市·中考真题）分解因式：_____．
【答案】
【分析】
直接根据平方差公式进行因式分解即可.
【详解】
，
故填
【点睛】
本题考查利用平方差公式进行因式分解，解题关键在于熟练掌握平方差公式.
62．（2021·江苏盐城市·中考真题）分解因式：a2+2a+1＝_____．
【答案】（a+1）2
【分析】
直接利用完全平方公式分解.
【详解】
a2+2a+1＝（a+1）2．
故答案为.
【点睛】
此题考查了因式分解—运用公式法，熟练掌握完全平方公式是解本题的关键.
63．（2021·江苏连云港市·中考真题）分解因式：____．
【答案】（3x＋1）2
【分析】
原式利用完全平方公式分解即可．
【详解】
解：原式＝（3x＋1）2，
故答案为：（3x＋1）2
【点睛】
此题考查了因式分解−运用公式法，熟练掌握完全平方公式是解本题的关键．
64．（2021·江苏苏州市·中考真题）因式分解______．
【答案】
【分析】
直接利用乘法公式分解因式得出答案．
【详解】
解：（x﹣1）2．
故答案为：（x﹣1）2．
【点睛】
此题主要考查了公式法分解因式，正确应用乘法公式是解题关键．
65．（2021·山东菏泽市·中考真题）因式分解：______．
【答案】
【分析】
先提取公因式，后采用公式法分解即可
【详解】
∵
=-a
=
故答案为: ．
【点睛】
本题考查了因式分解，熟记先提取公因式，后套用公式法分解因式是解题的关键．
66．（2021·黑龙江大庆市·中考真题）先因式分解，再计算求值：，其中．
【答案】，30
【分析】
先利用提公因式法和平方差公式进行因式分解，再代入x的值即可．
【详解】
解：，
当时，原式．
【点睛】
本题考查因式分解，掌握提公因式法和公式法是解题的关键．
67．（2019·江苏扬州·中考真题）计算：的结果是_____.
【答案】
【分析】逆用积的乘方运算法则以及平方差公式即可求得答案.
【解析】=
==(5-4)2018×=+2，故答案为+2.
【点睛】本题考查了积的乘方的逆用，平方差公式，熟练掌握相关的运算法则是解题的关键.
68.（2020·四川内江·中考真题）我们知道，任意一个正整数x都可以进行这样的分解：（m，n是正整数，且），在x的所有这种分解中，如果m，n两因数之差的绝对值最小，我们就称是x的最佳分解．并规定：．
例如：18可以分解成，或，因为，所以是18的最佳分解，所以．
（1）填空：；；
（2）一个两位正整数t（，，a，b为正整数），交换其个位上的数字与十位上的数字得到的新数减去原数所得的差为54，求出所有的两位正整数；并求的最大值；
（3）填空：①；②；
③；④．
【答案】（1）；1；（2）t为39，28，17；的最大值；（3）
【分析】（1）6＝1×6＝2×3，由已知可求＝；9=1×9=3×3，由已知可求=1；
（2）由题意可得：交换后的数减去交换前的数的差为：10b＋a−10a−b＝9（b−a）＝54，得到b−a＝6，可求t的值，故可得到的最大值；（3）根据的定义即可依次求解．
【解析】（1）6＝1×6＝2×3，∵6−1＞3−2，∴＝；9=1×9=3×3，
∵9−1＞3−3，∴=1，故答案为：；1；
（2）由题意可得：交换后的数减去交换前的数的差为：10b＋a−10a−b＝9（b−a）＝54，∴b−a＝6，
∵1≤a≤b≤9，∴b＝9，a＝3或b＝8，a＝2或b＝7，a＝1，∴t为39，28，17；
∵39＝1×39＝3×13，∴＝；28＝1×28＝2×14＝4×7，∴＝；
17＝1×17，∴；∴的最大值．
（3）①∵=20×21∴；
②=28×30∴；
③∵=56×30∴；
④∵=56×60∴，故答案为：．
【点睛】本题考查因式分解的应用；理解题意，从题目中获取信息，列出正确的代数式，再由数的特点求解是解题的关键．
题型七整式加减中的两种取值无关型问题
69.老师写出一个整式（ax2+bx-1）-（4x2+3x）（其中a、b为常数，且表示为系数），然后让同学给a、b赋予不同的数值进行计算，
(1)甲同学给出了一组数据，最后计算的结果为2x2-3x-1，则甲同学给出a、b的值分别是a=_______，b=_______；
(2)乙同学给出了a=5，b=-1，请按照乙同学给出的数值化简整式；
(3)丙同学给出一组数，计算的最后结果与x的取值无关，请直接写出丙同学的计算结果．
【答案】(1)6、0；(2)；(3)丙同学的计算结果是-1．
【解析】(1)解：（ax2+bx-1）-（4x2+3x）=ax2+bx-1-4x2-3x=（a-4）x2+（b-3）x-1，
∵甲同学给出了一组数据，最后计算的结果为2x2-3x-1，∴a-4=2，b-3=-3，
解得a=6，b=0，故答案为：6，0；
(2)解：由（1）（ax2+bx-1）-（4x2+3x）化简的结果是（a-4）x2+（b-3）x-1，
∴当a=5，b=-1时，
原式=（5-4）x2+（-1-3）x-1=x2-4x-1，
即按照乙同学给出的数值化简整式结果是x2-4x-1；
(3)解：由（1）（ax2+bx-1）-（4x2+3x）化简的结果是（a-4）x2+（b-3）x-1，
∵丙同学给出一组数，计算的最后结果与x的取值无关，
∴原式=-1，
即丙同学的计算结果是-1．
70.整式的计算：
(1)先化简，再求值，其中，．
(2)已知代数式，，．小丽说：“代数式的值与a，b的值无关．”她说得对吗？说说你的理由．
【答案】(1)；6；(2)小丽说得对，理由见详解
【解析】(1)解：原式=
==
将，代入
(2)
=
==7
小丽说得对．
71.在数学课上，王老师出示了这样一道题目：“当时，求多项式的值．”解完这道题后，小明指出是多余的条件．师生讨论后，一致认为小明的说法是正确的．请你说明正确的理由．
【答案】见解析
【详解】解：
．
∵化简后不含y，与y无关，
∴小明的说法正确．
72.老师布置了一道化简求值题，如下：求的值，其中，．
(1)小海准备完成时发现第一项的系数被同学涂了一下模糊不清了，同桌说他记得系数是．请你按同桌的提示，帮小海化简求值；
(2)科代表发现系数被涂后，很快把正确的系数写了上去。同学们计算后发现，老师给出的“”这个条件是多余的，请你算一算科代表补上的系数是多少？
【答案】(1)，．(2)．
【解析】(1)解：，
==，
当，时，原式=．
(2)设课代表填数的数为m，
，
=，
=，
∵老师给出的“”这个条件是多余的，
∴化简后与x无关，
∴，
解得．
题型八新定义问题
73．（2022·重庆）对多项式任意加括号后仍然只含减法运算并将所得式子化简，称之为“加算操作”，例如：，，…，给出下列说法：
①至少存在一种“加算操作”，使其结果与原多项式相等；
②不存在任何“加算操作”，使其结果与原多项式之和为0；
③所有的“加算操作”共有8种不同的结果．
以上说法中正确的个数为（ ）
A．0B．1C．2D．3
【答案】D
【分析】给添加括号，即可判断①说法是否正确；根据无论如何添加括号，无法使得的符号为负号，即可判断②说法是否正确；列举出所有情况即可判断③说法是否正确．
【详解】解：∵∴①说法正确
∵
又∵无论如何添加括号，无法使得的符号为负号∴②说法正确
∵当括号中有两个字母，共有4种情况，分别是、、、；
当括号中有三个字母，共有3种情况，分别是、、；
当括号中有四个字母，共有1种情况，
∴共有8种情况∴③说法正确∴正确的个数为3故选D．
【点睛】本题考查了新定义运算，认真阅读，理解题意是解答此题的关键．
74．（2021·重庆中考真题）如果一个自然数的个位数字不为，且能分解成，其中与都是两位数，与的十位数字相同，个位数字之和为，则称数为“合和数”，并把数分解成的过程，称为“合分解”．
例如，和的十位数字相同，个位数字之和为，
是“合和数”．
又如，和的十位数相同，但个位数字之和不等于，
不是“合和数”．
（1）判断，是否是“合和数”？并说明理由；
（2）把一个四位“合和数”进行“合分解”，即．的各个数位数字之和与的各个数位数字之和的和记为；的各个数位数字之和与的各个数位数字之和的差的绝对值记为．令，当能被整除时，求出所有满足条件的．
【答案】（1）不是“合和数”，是“合和数，理由见解析；（2）有，，，．
【分析】
（1）首先根据题目内容，理解“合和数”的定义：如果一个自然数的个位数字不为，且能分解成，其中与都是两位数，与的十位数字相同，个位数字之和为，则称数为“合和数”，再判断，是否是“合和数”；
（2）首先根据题目内容，理解“合分解”的定义．引进未知数来表示个位及十位上的数，同时也可以用来表示．然后整理出：，根据能被4整除时，通过分类讨论，求出所有满足条件的．
【详解】
解：（1）
不是“合和数”，是“合和数”．
，，
不是“合和数”，
，十位数字相同，且个位数字，
是“合和数”．
（2）设的十位数字为，个位数字为（，为自然数，且，），
则．
∴．
∴（是整数）．
，
，
是整数，
或，
①当时，
或，
或．
②当时，
或，
或．
综上，满足条件的有，，，．
【点睛】
本题考查了新定义问题，解题的关键是：首先要理解题中给出的新定义和会操作题目中所涉及的过程，结合所学知识去解决问题，充分考察同学们自主学习和运用新知识的能力．
75．（2022·重庆）若一个四位数的个位数字与十位数字的平方和恰好是去掉个位与十位数字后得到的两位数，则这个四位数为“勾股和数”．
例如：，∵，∴2543是“勾股和数”；
又如：，∵，，∴4325不是“勾股和数”．
(1)判断2022，5055是否是“勾股和数”，并说明理由；
(2)一个“勾股和数”的千位数字为，百位数字为，十位数字为，个位数字为，记，．当，均是整数时，求出所有满足条件的．
【答案】(1)2022不是“勾股和数”，5055是“勾股和数”；理由见解析
(2)8109或8190或4536或4563．
【分析】（1）根据“勾股和数”的定义进行验证即可；
（2）由“勾股和数”的定义可得，根据，均是整数可得，为3的倍数，据此得出符合条件的c，d的值，然后即可确定出M．
(1)解：2022不是“勾股和数”，5055是“勾股和数”；
理由：∵，，∴1022不是“勾股和数”；
∵，∴5055是“勾股和数”；
(2)∵为“勾股和数”，∴，∴，
∵为整数，∴，
∵为整数，
∴为3的倍数，
∴①，或，，此时或8190；
②，或，，此时或4563，
综上，M的值为8109或8190或4536或4563．
【点睛】本题以新定义为背景考查了整式混合运算的应用以及学生应用知识的能力，解题关键是要理解新定义，能根据条件找出合适的“勾股和数”．
76．（2022·重庆）对于一个各数位上的数字均不为0的三位自然数N，若N能被它的各数位上的数字之和m整除，则称N是m的“和倍数”．
例如：∵，∴247是13的“和倍数”．
又如：∵，∴214不是“和倍数”．
(1)判断357，441是否是“和倍数”？说明理由；
(2)三位数A是12的“和倍数”，a，b，c分别是数A其中一个数位上的数字，且．在a，b，c中任选两个组成两位数，其中最大的两位数记为，最小的两位数记为，若为整数，求出满足条件的所有数A．
【答案】(1)357不是15“和倍数”，441是9的“和倍数”；理由见解析
(2)数A可能为732或372或516或156
【分析】（1）根据题目中给出的“和倍数”定义进行判断即可；
（2）先根据三位数A是12的“和倍数”得出，根据，是最大的两位数，是最小的两位数，得出，（k为整数），结合得出，根据已知条件得出，从而得出或，然后进行分类讨论即可得出答案．
(1)解：∵，∴357不是15“和倍数”；
∵，∴441是9的“和倍数”．
(2)∵三位数A是12的“和倍数”，∴，
∵，∴在a，b，c中任选两个组成两位数，其中最大的两位数，最小的两位数，∴，
∵为整数，设（k为整数），则，
整理得：，根据得：，
∵，∴，解得，
∵“和倍数”是各数位上的数字均不为0的三位自然数，
∴，∴，∴，把代入得：
，整理得：，∵，k为整数，∴或，
当时，，∵，∴，，
，，，或，，，
要使三位数A是12的“和倍数”，数A必须是一个偶数，
当，，时，组成的三位数为或，
∵，∴是12的“和倍数”，
∵，∴是12的“和倍数”；
当，，时，组成的三位数为或，
∵，∴不是12的“和倍数”，
∵，∴不是12的“和倍数”；
当时，，∵，∴，
，，，组成的三位数为516或156，
∵，∴是12的“和倍数”，
∵，∴是12的“和倍数”；
综上分析可知，数A可能为732或372或516或156．
【点睛】本题主要考查了新定义类问题，数的整除性，列代数式，利用数位上的数字特征和数据的整除性，是解题的关键，分类讨论是解答本题的重要方法，本题有一定的难度．