




所属成套资源:2024秋北师大版数学七年级上册全册课件
2024秋北师大版数学七年级上册第3章 回顾与思考(归纳)课件
展开
这是一份2024秋北师大版数学七年级上册第3章 回顾与思考(归纳)课件,共28页。
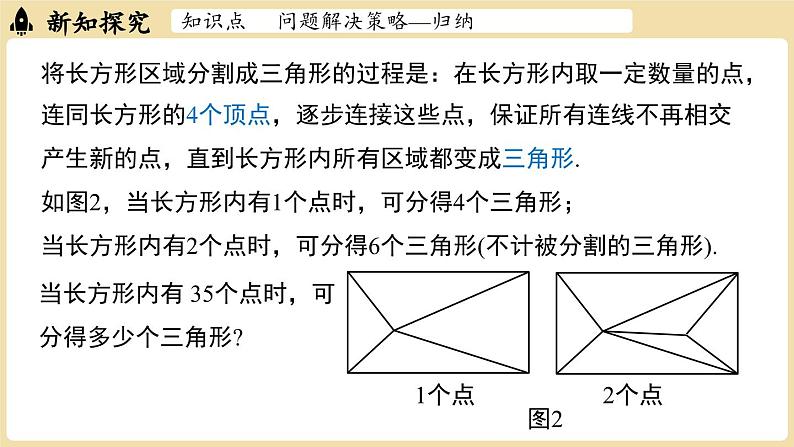
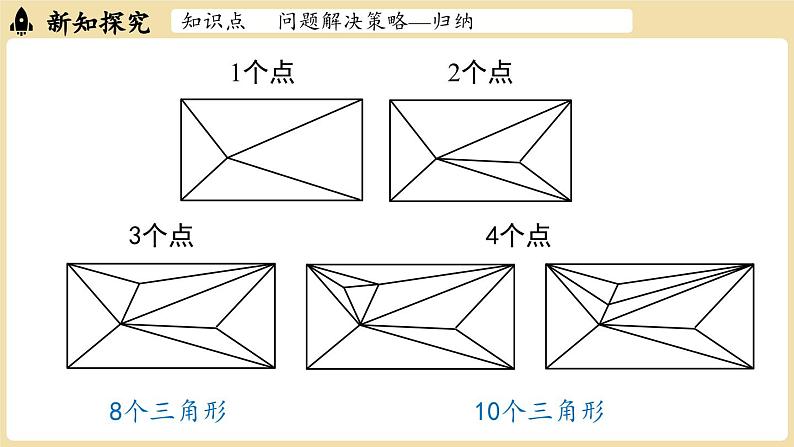
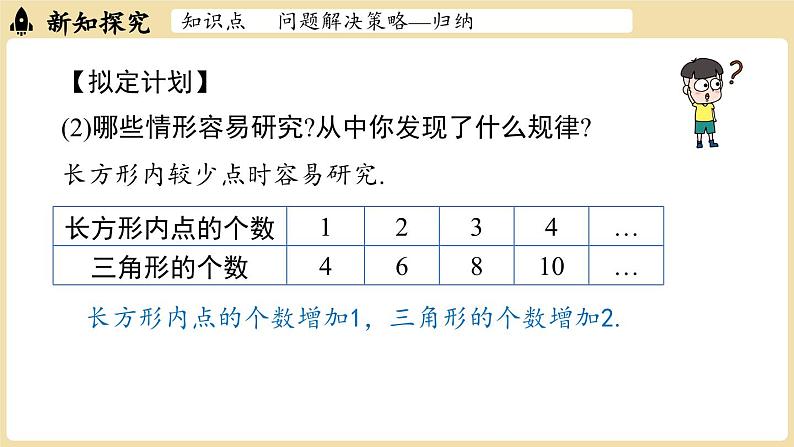
第三章 整式及其加减问题解决策略—归纳七上数学 BSD例1 “低多边形风格”是一种数字艺术设计风格.它将整个区域分割为若干三角形,通过把相邻三角形涂上不同颜色,产生立体及光影的效果,随着三角形数量增加,效果更为斑斓绚丽(如图1).知识点 问题解决策略—归纳 图1知识点 问题解决策略—归纳 将长方形区域分割成三角形的过程是:在长方形内取一定数量的点,连同长方形的4个顶点,逐步连接这些点,保证所有连线不再相交产生新的点,直到长方形内所有区域都变成三角形.如图2,当长方形内有1个点时,可分得4个三角形;当长方形内有2个点时,可分得6个三角形(不计被分割的三角形). 当长方形内有 35个点时,可分得多少个三角形?1个点 2个点图2知识点 问题解决策略—归纳 【理解问题】(1)先动手画一画,感受分割三角形的过程.(2)已知条件是什么?目标是什么?已知条件:目标:当长方形内有 35个点时,可分得多少个三角形?知识点 问题解决策略—归纳 【拟定计划】(1)直接研究“长方形内有 35个点”的情形,你遇到了什么困难?难以画出,无法求得其三角形数.(2)哪些情形容易研究?从中你发现了什么规律?长方形内较少点时容易研究.知识点 问题解决策略—归纳 1个点 2个点3个点 4个点10个三角形8个三角形知识点 问题解决策略—归纳 【拟定计划】(2)哪些情形容易研究?从中你发现了什么规律?长方形内较少点时容易研究. 长方形内点的个数增加1,三角形的个数增加2.知识点 问题解决策略—归纳 解:猜想是合理的.在长方形内已经有n个点的情况下,新增的一个点要么在某个三角形内部,要么在某条线段上.点在某个三角形内部时:连接该点和三角形的顶点,原来的1个三角形分成3个小三角形,三角形的个数增加2;点在某条线段上时,连接该点和它所在两个三角形的顶点,三角形的个数同样增加2.(3)你发现的规律正确吗?你能给出合理的解释吗?知识点 问题解决策略—归纳 【实施计划】长方形内点的个数增加 1,三角形的个数增加 2.当长方形内有35个点时,分得的三角形的个数是4+2×34=72.知识点 问题解决策略—归纳 【回顾反思】(1)如果长方形内有100个点呢?一般地,如果长方形内有n个点呢?长方形内有100个点:长方形内有n个点:4+2×(100-1)=202.4+2×(n-1)=2n+2.知识点 问题解决策略—归纳 【回顾反思】(2) 从简单的情形开始思考有什么好处?通过简单情形归纳一般性结论,你有哪些经验?从简单情形入手往往更易看清问题的本质,便于揭示问题的规律.知识点 问题解决策略—归纳 在运用归纳策略寻找规律时,要先在若干简单情形中寻找相应的规律.初步发现规律后,可以通过更多的情形验证,再考虑一般情况.最后,试着给出合理的解释,并用数学语言简洁地表达规律.知识点 问题解决策略—归纳 例2 2022年北京冬奥会开幕式主火炬台由96块小雪花形态和6 块橄榄枝构成的巨型“雪花”形态,在数学上,我们可以通过“分形”近似地得到雪花的形状.将一个边长为1的等边三角形(如图①)的每一边三等分,以居中那条线段为底边向外作等边三角形,并去掉所作的等边三角形的一条边,得到一个六角星(如图②),称为第1次分形.图① 图②知识点 问题解决策略—归纳 接着对每个等边三角形凸出的部分继续上述过程,即在每条边三等分后的中段向外画等边三角形,得到一个新的图形(如图③),称为第2次分形.不断重复这样的过程,就得到了“科赫雪花曲线”.猜想第4次分形后得到的“雪花曲线”的边数是多少?图① 图② 图③知识点 问题解决策略—归纳 【解决方案】(1)先研究第1次和第2次分形的情形.(2)几种简单情形的数据如下表:12条边48条边知识点 问题解决策略—归纳 发现的规律:每一次分形后,得到的“雪花曲线”的边数是前一个“雪花曲线”边数的4 倍.知识点 问题解决策略—归纳 (3)验证猜想是否正确.正确.首先,每条边上的分形变化是相同的,因此只需关注一条边的变化规律即可.每条边分形时,首先被等分为3条边,而中间的一条边凸出变成2条边,因此是原来边数的4倍,每条边都是如此因此分形1次后总边数是上一次总边数的4倍.知识点 问题解决策略—归纳 (4)计算.根据分析,第4次分形后得到的“雪花曲线”的边数为3×4×4×4×4 =768.知识点 问题解决策略—归纳 【回顾反思】你还能提出并解决哪些问题?答案不唯一,如:若图①中等边三角形的边长为1,根据以上步骤进行操作,第n次分形后得到的“雪花曲线”的边长是多少?(用含n的代数式表示)知识点 问题解决策略—归纳 随堂练习1. 32024的个位数字是多少?解:31=3,32=9,33=27,34=81,35=243,36=729,37=2 187,…根据规律可知,3n的个位数字以3,9,7,1为一个循环.又因为 2024 ÷4 =506,所以32024的个位数字是 1.随堂练习2.某类简单化合物中前6种化合物的分子结构模型如图所示,按照这一规律,第60种化合物的分子结构模型中有多少个氢原子(H)?随堂练习解:第1种化合物的分子结构模型中有4个氢原子;第2种化合物的分子结构模型中有4+2=6(个)氢原子;第3种化合物的分子结构模型中有4+2+2=8(个)氢原子;第4 种化合物的分子结构模型中有4+2×(4﹣1)=10(个)氢原子; ……第60种化合物的分子结构模型中有4+2×(60﹣1)=122(个)氢原子.随堂练习3.如图,将一根绳子折成三段,然后按如图所示的方式剪开,剪1刀,绳子变为4段;剪2刀,绳子变为7段.(1)剪12刀,绳子变为多少段?解:剪1刀,绳子变成4 段;剪2刀,绳子变成4+3=7 (段);剪3刀,绳子变成4+3+3=10 (段);……剪12刀,绳子变成4+3×(12﹣1)=37 (段).随堂练习3.如图,将一根绳子折成三段,然后按如图所示的方式剪开,剪1刀,绳子变为4段;剪2刀,绳子变为7段. (2)有可能正好剪得 101段吗? 随堂练习4.由1,3,5,7,9,11,13,15,17,19,…组成的三角形数阵如图所示,则第10行的10个数的和是多少?13 57 9 1113 15 17 1923 25 27 29……随堂练习13 57 9 1113 15 17 1921 23 25 27 29……解:由数阵可得,第1行的1个数的和是1=13,第2行的2个数的和是8=23,第3 行的3个数的和是27 =33,第4 行的4个数的和是 64 =43……第10行的 10 个数的和是 103= 1 000.从几种特殊情形出发,进而找到一般规律是发现数学结论、解决数学问题的一种重要策略,这种问题解决策略就是归纳.在运用归纳策略寻找规律时,要先在若干简单情形中寻找规律,通过验证后再考虑一般情况,最后给出合理的解释,并用数学语言表达规律.






