

山西省阳泉市部分学校2024-2025学年上学期期中考试九年级数学试卷
展开(满分120分,练习时间120分钟)
第I卷 选择题(共30分)
一、选择题(本大题共10个小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项符合题目要求)
1.下列二次根式中,与是同类二次根式的是( )
A.B.C.D.
2.已知关于x的一元二次方程,若,则下列各数中是该方程的根的是( )
A.1B.C.2D.0
3.在数学史上,有很多著名的几何图形用来验证数学知识的产生过程.如图所示的图案,是由一连串公共顶点为O的直角三角形拼接而成,若,则图中直角三角形之间存在的变换关系是( )
A.图形的平移B.图形的旋转C.图形的全等D.图形的相似
4.利用配方法解方程时,将该方程化为的形式,然后利用直接开平方法求解,这个过程体现的数学思想是( )
A.数形结合思想B.转化思想C.整体思想D.公理化思想
5.如果,那么下列比例式正确的是( )
A.B.C.D.
6.若等腰三角形一条边的长为3,另两条边的长分别是关于x的一元二次方程的两个根,则k的值是( )
A.27B.36C.27或36D.18
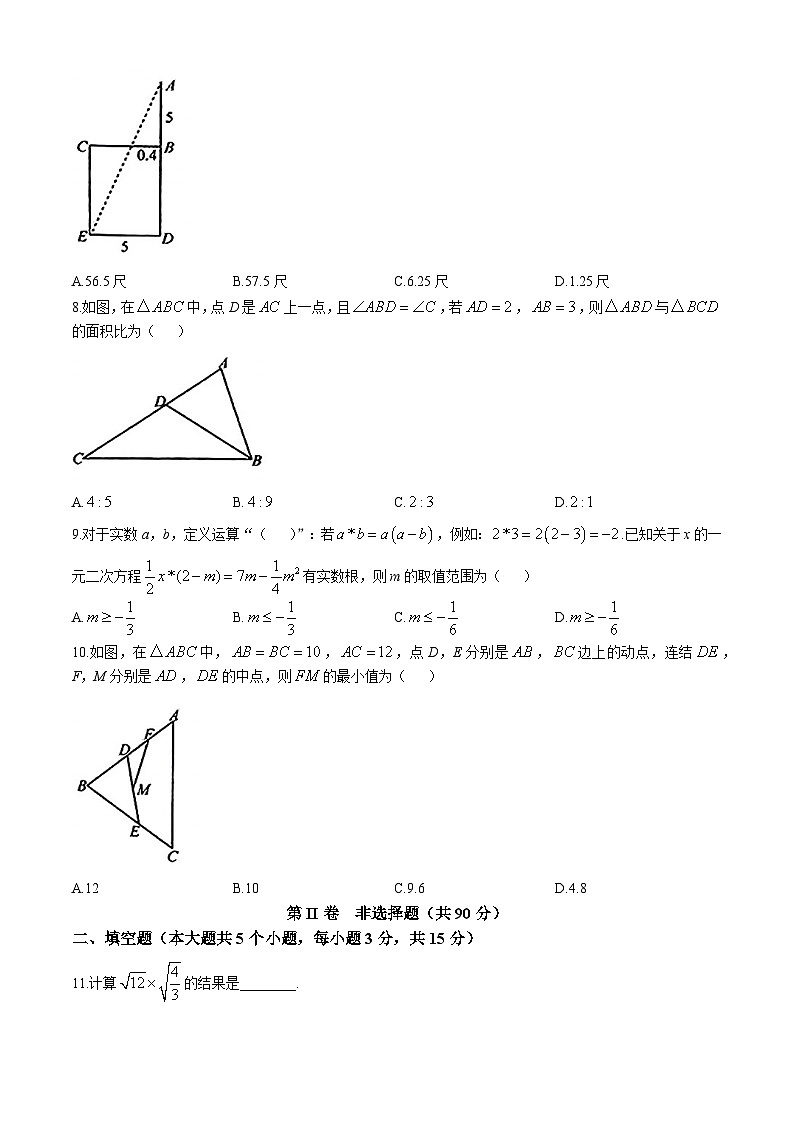
7.我国古代数学《九章算术》中有一道“井深几何”的问题:“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸(1尺等于10寸),问井深几何?”根据题意画出如图示意图,则并深为( )
A.56.5尺B.57.5尺尺尺
8.如图,在中,点D是上一点,且,若,,则与的面积比为( )
A.B.C.D.
9.对于实数a,b,定义运算“( )”:若,例如:.已知关于x的一元二次方程有实数根,则m的取值范围为( )
A.B.C.D.
10.如图,在中,,,点D,E分别是,边上的动点,连结,F,M分别是,的中点,则的最小值为( )
A.12B.10C.9.6D.4.8
第II卷 非选择题(共90分)
二、填空题(本大题共5个小题,每小题3分,共15分)
11.计算的结果是________.
12.如图,直线,若,,,那么的长为________.
13.某种小家电在两年内提价两次后每个的价格比两年前增加了44%,则平均每次提价的百分率为________.
14.如图,小明在A时测得某树的影长为3m,B时又测得该树的影长为2m,若两次日照的光线互相垂直,则树的高度为________m.
15.如图,在中,,,,点D是边上的一点,过点D作,交于点F,作的平分线交于点E,连接.若的面积是2,则的值是________.
三、解答题(本大题共8个小题,共75分.解答应写出文字说明,证明过程或演算步骤)
16.(每小题5分,共10分)
(1)计算:
(2)解方程:
17.(本题10分)图①、图②、图③都是的网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.点A,B,C均在格点上.在图①、图②、图③给定的网格中,仅用无刻度的直尺,按下列要求完成作图,并保留作图痕迹.
图① 图② 图③
(1)在图①中,以点C为位似中心,将放大到原来的2倍;
(2)在图②中,在线段上作点D,使得;
(3)在图③中,作,且相似比为.
18.(本题8分)玉米俗称玉米棒子、苞米,是我国第一大粮食作物,也是全世界公认的“黄金作物”.政府鼓励农民种植玉米,一亩地每年补贴300元.经调查:我省玉米实验田平均亩产量约1300千克,市场销售价为每千克1.2元,除购买种子、播种、施肥、浇水、收割等成本费用外(随种植亩数的变化而变化),种植一亩玉米的净利润达到1360元.
(1)求种植一亩玉米的成本需要多少元;
(2)某农场现有15亩实验田,计划种植玉米和蔬菜,根据经验调查发现:按2023年种植一亩玉米的成本来计算,以后每多种植1亩,平均每亩的成本会减少20元,2024年农场计划投入3200元的成本种植玉米,问:该农场计划种植几亩玉米?
19.(本题7分)如图,在中,点D在边上,,点E在边上,.
(1)求证:.
(2)若,,求的长.
20.(本题8分)项目化学习
项目主题:测量树的高度.
分析探究:树的高度不能直接测量,需要借助一些工具,比如小镜子,标杆,皮尺,小木棒,自制的直角三角形硬纸板,确定方案后,还要画出测量示意图,并实地进行测量,得到具体数据,从而计算出树的高度.
成果展示:下面是某小组进行交流展示时的部分测量方案及测量数据:
请同学们继续完善上述成果展示:
任务一:根据测量数据,求出树的高度;
任务二:写出求树的高度时所利用的数学知识________________________________________.(写出一个即可)
21.(本题8分)阅读下列材料,并按要求完成相应的任务.
两千多年前,古希腊数学家欧多克索斯(Eudxus,约前400-前347)发现:如图1,将一条线段分割成长、短两条线段,,若较短线段与较长线段的比等于较长线段与原线段的比,即(此时线段叫做线段,的比例中项),则可得出这一比值等于,这种分割为黄金分割,这个比值为黄金比,P为线段的黄金分割点.
图1
采用如下方法可以得到黄金分割点:如图2,设是已知线段,经过点B作,且,连接,在上截取,在上截取,则C就是线段的黄金分割点.
任务:
图2
(1)求证:C是线段的黄金分割点.
(2)若,则的长为________.
22.(本题12分)综合与实践
(1)如图①,在中,,,点D在边上,点E在边上.若,求证:.
图①
(2)如图②,在矩形中,,,点E在边上,连接,过点E作,交于点F.
图②
i)若,求的长;
ii)若点F恰好与点D重合,求的长.
23.(本题12分)综合与探究
如图1,在矩形中,,,点E是对角线上任意一点,交于点G,交于点F.
(1)当点E为的中点时,________.
图1
(2)如图2,将四边形绕点B逆时针旋转,连结,.在旋转过程中,是否发生变化,若不变化,求出的值,若发生变化,请说明理由.
图2
(3)如图3,将四边形绕点B逆时针旋转,连结,.请直接写出旋转过程中的值.
图3
九年级数学答案
一、
1、C2、A3、D4、B5、C6、B7、B8、A9、D10、D
二、
11、412、13、20%14、
15、
三、
16、解:(1)
(2),,,,,.
17、(1)如图,即为所求
(2)如图,点D即为所求
(3)如图,即为所求
18、(1)设种植一亩玉米的成本需要x元,
依题意得:,
解得.
答:种植一亩玉米的成本最高需要500元.
(2)设该农场计划种植y亩玉米,则每亩的成本为
依题意得:,整理得:,
解得:,(不合题意,舍去)。
答:该农场计划种植10亩玉米.
19、(1)证明:∵,∴.
∵,,又,
∴,
∵,∴.
(2)∵,∴,即,解得,.
20、(1)解:如图,过点C作于点G,交于点H.
则四边形与四边形是矩形.
∴,,.
.
由题意得,
∴.
∴,
∴,
∴.
∴.
(2)答案不唯一,例:相似三角形的性质与判定
21、(1)证明:设,则,由勾股定理得,
∵,,
∴,
∴,
∴C是线段的黄金分割点;
(2)当时,由(1)知,,
∴.
22、(1)证明:∵,,
∴.∴.
∵,∴.∴.
∴.
(2)解:i)∵四边形是矩形,
∴.∴.
∵,∴.
∴.∴.∴.
∵,
∴,.
∴,
∴.
∴CF的长为.
ii)设,则.由①得.
∴,
∴,即.
整理,得.解得,.
∴的长为2cm或8cm.
23、(1)∵,
∴,
∵,,
∴
在中,,,
∴,
∴,故答案为:.
(2)没有变化,连接,如图:
由旋转的性质可知,,和长度不变,由(1)知,,
∴,∴;
(3)连接,如图:
在图中,,∴,由旋转的性质可知,,和长度不变,
∴,∴.测量工具
标杆,皮尺
测量方案
选一名同学作为观测者,在观测者与树之间的地面直立一根标杆,使树的顶端、标杆的顶端与观测者的眼睛恰好在一条直线上.这时再测出观测者的脚到树底端的距离,以及观测者的脚到标杆底端的距离,然后测出标杆的高.
测量示意图
测量数据
线段表示树,标杆,观测者的眼睛到地面的距离,观测者的脚到树底端的距离,观测者的脚到标杆底端的距离.
……
山西省阳泉市矿区多校2024-2025学年九年级上学期期中测试数学试卷: 这是一份山西省阳泉市矿区多校2024-2025学年九年级上学期期中测试数学试卷,共8页。试卷主要包含了已知一元二次方程,配方后可化为等内容,欢迎下载使用。
山西省阳泉市矿区多校2024-2025学年八年级上学期期中测试数学试卷: 这是一份山西省阳泉市矿区多校2024-2025学年八年级上学期期中测试数学试卷,文件包含数学试卷pdf、数学答案docx等2份试卷配套教学资源,其中试卷共7页, 欢迎下载使用。
山西省阳泉市平定县第二中学校2024届九年级上学期期中考试数学试卷(含答案): 这是一份山西省阳泉市平定县第二中学校2024届九年级上学期期中考试数学试卷(含答案),共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












