江苏南通市崇川初级中学2024-2025学年八上数学网络提高班面积问题专项训练【含答案】

这是一份江苏南通市崇川初级中学2024-2025学年八上数学网络提高班面积问题专项训练【含答案】，共12页。

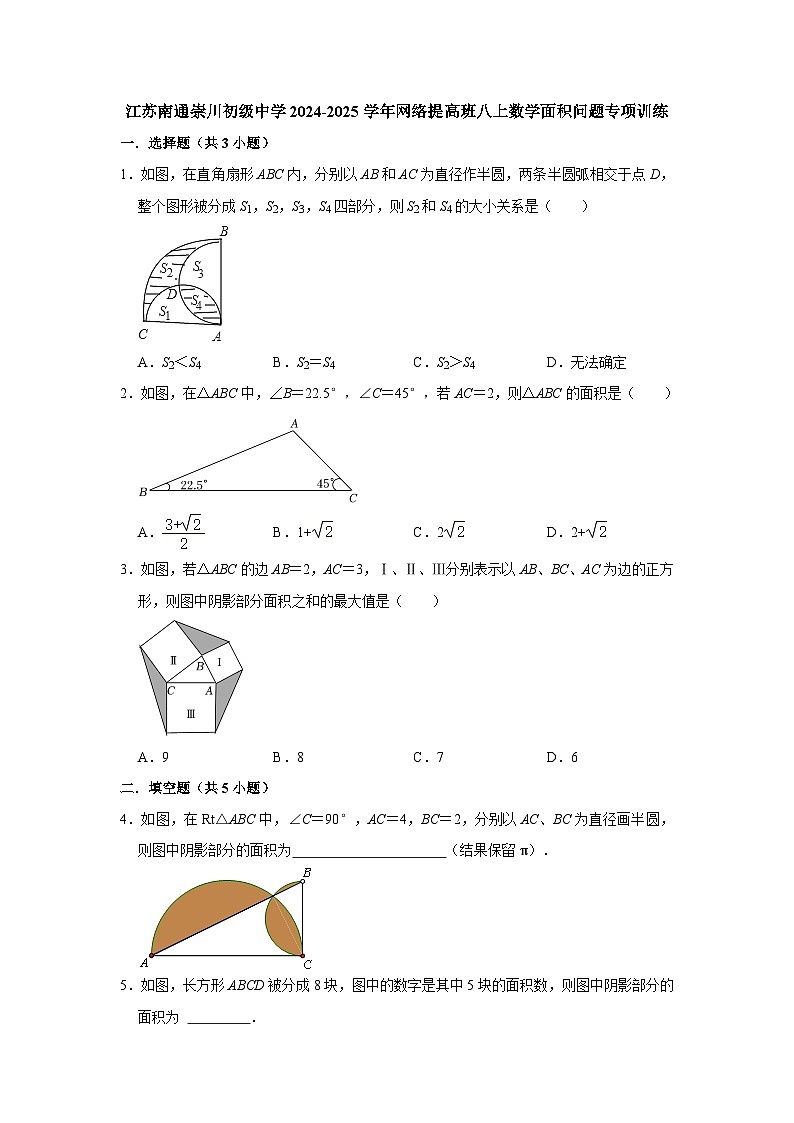
A．S2＜S4B．S2＝S4C．S2＞S4D．无法确定
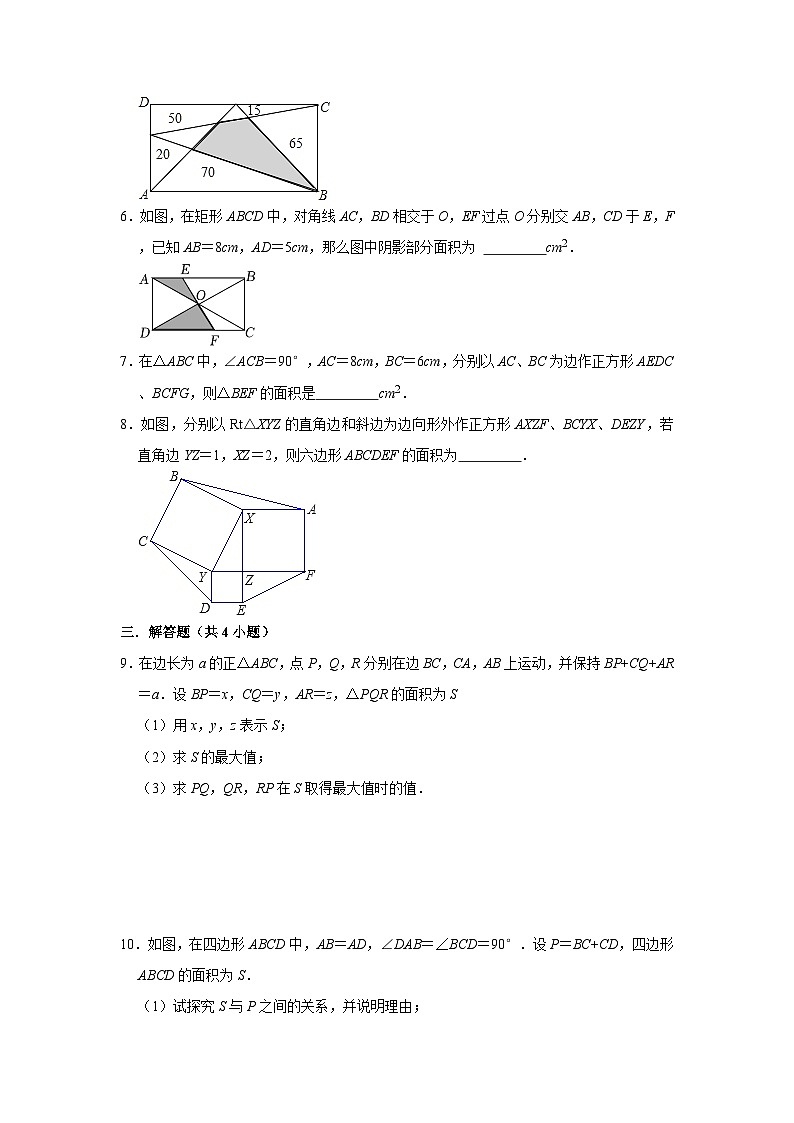
2．如图，在△ABC中，∠B＝22.5°，∠C＝45°，若AC＝2，则△ABC的面积是（ ）
A．B．1+C．2D．2+
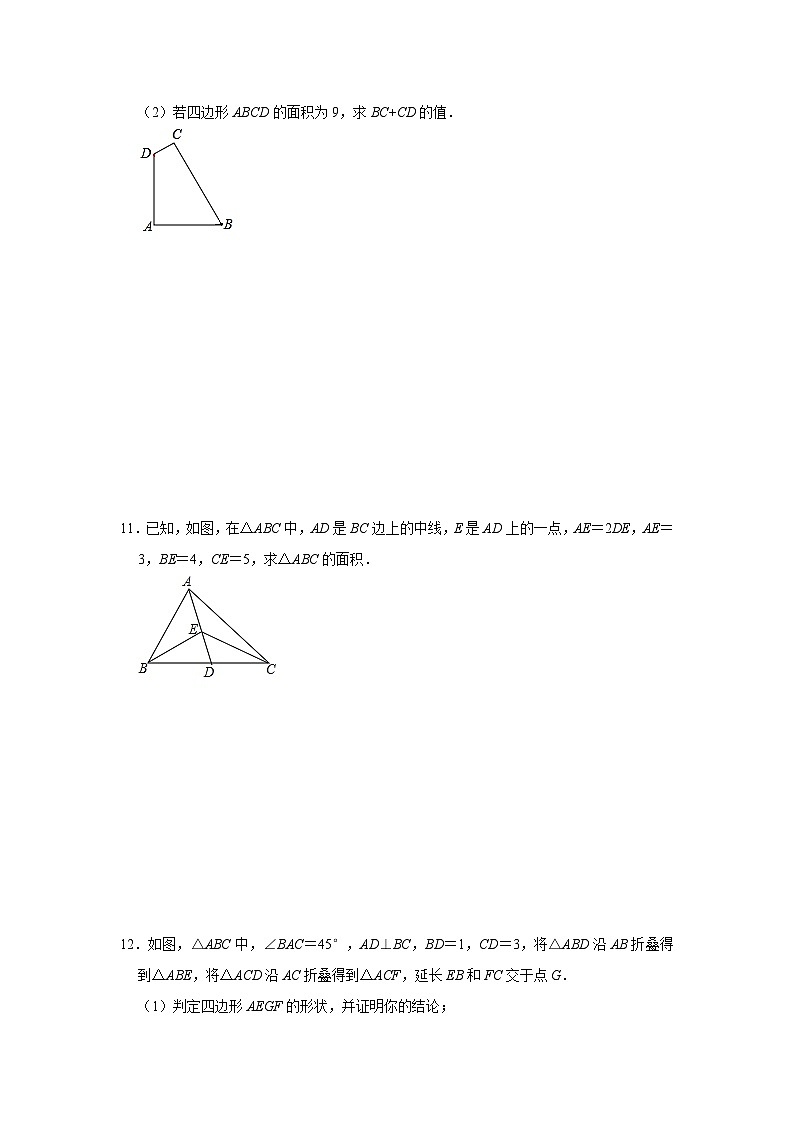
3．如图，若△ABC的边AB＝2，AC＝3，Ⅰ、Ⅱ、Ⅲ分别表示以AB、BC、AC为边的正方形，则图中阴影部分面积之和的最大值是（ ）
A．9B．8C．7D．6
二．填空题（共5小题）
4．如图，在Rt△ABC中，∠C＝90°，AC＝4，BC＝2，分别以AC、BC为直径画半圆，则图中阴影部分的面积为 （结果保留π）．
5．如图，长方形ABCD被分成8块，图中的数字是其中5块的面积数，则图中阴影部分的面积为 ．
6．如图，在矩形ABCD中，对角线AC，BD相交于O，EF过点O分别交AB，CD于E，F，已知AB＝8cm，AD＝5cm，那么图中阴影部分面积为 cm2．
7．在△ABC中，∠ACB＝90°，AC＝8cm，BC＝6cm，分别以AC、BC为边作正方形AEDC、BCFG，则△BEF的面积是 cm2．
8．如图，分别以Rt△XYZ的直角边和斜边为边向形外作正方形AXZF、BCYX、DEZY，若直角边YZ＝1，XZ＝2，则六边形ABCDEF的面积为 ．
三．解答题（共4小题）
9．在边长为a的正△ABC，点P，Q，R分别在边BC，CA，AB上运动，并保持BP+CQ+AR＝a．设BP＝x，CQ＝y，AR＝z，△PQR的面积为S
（1）用x，y，z表示S；
（2）求S的最大值；
（3）求PQ，QR，RP在S取得最大值时的值．
10．如图，在四边形ABCD中，AB＝AD，∠DAB＝∠BCD＝90°．设P＝BC+CD，四边形ABCD的面积为S．
（1）试探究S与P之间的关系，并说明理由；
（2）若四边形ABCD的面积为9，求BC+CD的值．
11．已知，如图，在△ABC中，AD是BC边上的中线，E是AD上的一点，AE＝2DE，AE＝3，BE＝4，CE＝5，求△ABC的面积．
12．如图，△ABC中，∠BAC＝45°，AD⊥BC，BD＝1，CD＝3，将△ABD沿AB折叠得到△ABE，将△ACD沿AC折叠得到△ACF，延长EB和FC交于点G．
（1）判定四边形AEGF的形状，并证明你的结论；
（2）求△ABC的面积．
参考答案与试题解析
一．选择题（共3小题）
1．【解答】解：设AB＝AC＝2a，根据题意得，
S2＝S扇形ACB﹣S半圆AB﹣S半圆AC+S4＝﹣2××π×a2+S4＝S4，
所以S2＝S4．
故选：B．
2．【解答】解：如图，过点A作AD⊥AC于A，交BC于D，过点A作AE⊥BC于E，
∵∠C＝45°，
∴△ADC是等腰直角三角形，
∴AD＝AC＝2，∠ADC＝45°，CD＝AC＝2，
∵∠ADC＝∠B+∠BAD，∠B＝22.5°，
∴∠DAB＝22.5°，
∴∠B＝∠DAB，
∴AD＝BD＝2，
∵AD＝AC，AE⊥CD，
∴DE＝CE，
∴AE＝CD＝，
∴△ABC的面积＝•BC•AE＝××（2+2）＝2+．
故选：D．
3．【解答】解：如图，把△CFH绕点C顺时针旋转90°，使CF与BC重合，H旋转到H'的位置，
∵四边形ACHD为正方形，
∴∠ACH＝90°，CA＝CH＝CH′，
∴A、C、H'在一直线上，且BC为△ABH'的中线，
∴S△CHF＝S△BCH′＝S△ABC，
同理：S△ADE＝S△BGI＝S△ABC，
所以阴影部分面积之和为S△ABC的3倍，
又∵AB＝2，AC＝3，
∴当AB⊥AC时，△ABC的面积最大，
此时S△ABC＝＝3，S阴影部分面积＝3S△ABC＝3×3＝9，
故选：A．
二．填空题（共5小题）
4．【解答】解：
设各个部分的面积为：S1、S2、S3、S4、S5，如图所示，
∵两个半圆的面积和是：S1+S5+S4+S2+S3+S4，△ABC的面积是S3+S4+S5，阴影部分的面积是：S1+S2+S4，
∴图中阴影部分的面积为两个半圆的面积减去三角形的面积．
即阴影部分的面积＝π×4+π×1﹣4×2÷2＝π﹣4．
5．【解答】解：设未知的三块面积分别为x，y，z（如图）
则，即
由①+②解得 y＝85
故答案为85
6．【解答】解：在矩形ABCD中，OA＝OC、AB∥CD，
∴∠EAO＝∠FCO，
在△EAO与△FCO中，
，
∴△EOA≌△FOC（ASA），
∴S阴影部分＝S△DOC＝S矩形ABCD＝×8×5＝10（cm2），
故答案为：10．
7．【解答】解：连接EC并延长交BF于点H，
∵四边形AEDC、BCFG均是正方形，
∴∠DCA＝∠BCF＝90°，
∵∠ACB＝90°，
∴∠DCF＝90°，
在△ABC与△DFC中，
，
∴△ABC≌△DFC（SAS），
∴DF＝AB，∠CDF＝∠CAB，
∴∠EDF＝∠EAB，
在△EDF与△EAB中，
，
∴△EDF≌△EAB（SAS），
∴EF＝EB，
∴△BEF是等腰三角形，
∵CF＝CB，
∴△BCF是等腰三角形，
∴EH是BF的垂直平分线，
∵AC＝8cm，BC＝6cm，
∴CE＝＝8cm，BF＝＝6cm，
∴CH＝BF＝3cm，
∴BH＝CE+CH＝8+3＝11cm，
∴S△BEF＝BF•EH＝×6×11＝66cm2．
故答案为：66．
8．【解答】解：在Rt△XYZ中，根据勾股定理得：
XY2＝YZ2+XZ2＝12+22＝5，
∴XY＝．
∴sin∠YXZ＝，sin∠XYZ＝，
所以得：
正方形AXZF的面积＝2×2＝4，
正方形DEZY的面积＝1×1＝1，
正方形BCYX的面积＝×＝5，
△XYZ的面积＝×1×2＝1，
△EFZ的面积＝×1×2＝1，
又∠AXB＝360°﹣90°﹣90°﹣∠YXZ＝180°﹣∠YXZ，
同理：∠DYC＝180°﹣∠XYZ，
已知正方形AXZF、BCYX、DEZY，
∴AX＝2，DY＝1，BX＝CY＝，
∴△ABX的面积＝AX•BX•sin∠AXB＝AX•BX•sin（180°﹣∠YXZ）
＝AX•BX•sin∠YXZ＝×2××＝1，
同理：△CDY的面积＝CY•DY•sin∠XYZ＝××1×＝1．
六边形ABCDEF的面积＝正方形AXZF的面积+正方形DEZY的面积+正方形BCYX的面积+△XYZ的面积+△EFZ的面积+△ABX的面积+△CDY的面积
＝4+1+5+1+1+1+1＝14．
故答案为：14．
三．解答题（共4小题）
9．【解答】解：（1）过点A与R作AD⊥BC于D，RE⊥BC于E，
∵正△ABC的边长为a，
∴在Rt△ABD中，sin60°＝＝，
∴AD＝a，
∴S△ABC＝BC•AD＝a2，
∴在Rt△RBE中，sin60°＝＝，
∵BP＝x，CQ＝y，AR＝z，
∴RB＝a﹣z，
∴RE＝（a﹣z），
∴S△RBP＝BP•RE＝x•（a﹣z）＝x（a﹣z），
同理：S△PQC＝y（a﹣x），S△ARQ＝z（a﹣y），
∵x+y+z＝a，
∴S△PQR＝S△ABC﹣S△RBP﹣S△PQC﹣S△ARQ，
＝[a2﹣x（a﹣z）﹣y（a﹣x）﹣z（a﹣y）]，
＝[a2﹣a（x+y+z）+xz+xy+yz]，
＝（a2﹣a2+xy+xz+yz）＝（xy+xz+yz）；
∴S＝xy+xz+yz；
（2）∵3（xy+yz+xz）＝（xy+yz+xz）+2xy+2yz+2xz≤x2+y2+y2+z2+x2+y2+2xy+2yz+2xz＝x2+y2+z2+2xy+2yz+2xz＝（x+y+z）2＝a2，
∴xy+yz+xz≤a2，
∴S＝（xy+xz+yz）≤×a2＝a2，
∴当x＝y＝z＝a时，S的最大值为：a2；
（3）当x＝y＝z＝a时，S取最大值，
即：PQ＝QR＝RP＝a．
10．【解答】解：（1）S＝P2，理由如下：
连接BD，如图所示：
∵∠DAB＝∠BCD＝90°，
∴BD2＝AD2+AB2＝DC2+BC2；
∵AD＝AB，
∴2AD2＝DC2+BC2，
∴S＝+＝+＝+＝（DC+BC）2＝P2；
（2）根据题意得：P2＝9，
∴P2＝36，
解得：P＝6，或P＝﹣6（舍去），
即BC+CD＝6．
11．【解答】解：延长AD到F，使ED＝DF，连接BF，
∴EF＝2DE，
∵AE＝2DE，AE＝3，
∴EF＝AE＝3，
在△BDF与△CED中，，
∴△BDF≌△CDE，
∴BF＝CE＝5，
∵BE＝4，
∴BE2+EF2＝42+32＝52＝BF2，
∴∠BEF＝90°，
∴S△BCE＝S△BEF＝×3×4＝6，
∵AE＝2DE，
∴S△ABE+S△ACE＝2S△BCE＝12，
∴S△ABC＝18．
12．【解答】（1）解：四边形AEGF是正方形；理由如下：
∵AD⊥BC，
∴∠ADB＝∠ADC＝90°，
由折叠的性质得：∠BAE＝∠BAD，∠E＝∠ADB＝90°，AE＝AD，
∠FAC＝∠DAC，∠F＝∠ADC＝90°，AF＝AD，
∴AE＝AF，
∵∠BAC＝45°，
∴∠EAF＝90°，
∴四边形AEGF是矩形，
又∵AE＝AF，
∴四边形AEGF是正方形；
（2）解：∵四边形AEGF是正方形，
∴∠G＝90°，
设AD＝x，
则GF＝GE＝AE＝x，
由折叠的性质得：BE＝BD＝1，CF＝CD＝3，
∴BC＝4，BG＝x﹣1，GC＝x﹣3，
在Rt△BGC中，根据勾股定理得：GC2+BG2＝BC2，
即（x﹣3）2+（x﹣1）2＝42，
解得：x＝2±（负值舍去），
∴AD＝2+，
∴△ABC的面积＝BC×AD＝×4×（2+）＝4+2．声明：试题解析著