江苏淮安市凌桥中学2024-2025学年八上创优班数学几何最值问题-专项训练【含答案】

这是一份江苏淮安市凌桥中学2024-2025学年八上创优班数学几何最值问题-专项训练【含答案】，共23页。

A．B．C．D．
2．△ABC中，AB＝15，BC＝14，AC＝13，则△ABC的面积是（ ）
A．96B．120C．84D．60
3．如图，Rt△ABC中，∠C＝90°，CD⊥AB于点D，AB＝13，CD＝6，则AC+BC等于（ ）
A．5B．C．D．
二．填空题（共6小题）
4．如图，在△ABC中，∠BAC＝90°，AB＝3，AC＝4，AD平分∠BAC交BC于D，则BD的长为 ．
5．在Rt△ABC中，∠C＝90°，△ABC的周长为+2，其中斜边的长为2，则这个三角形的面积为 ．
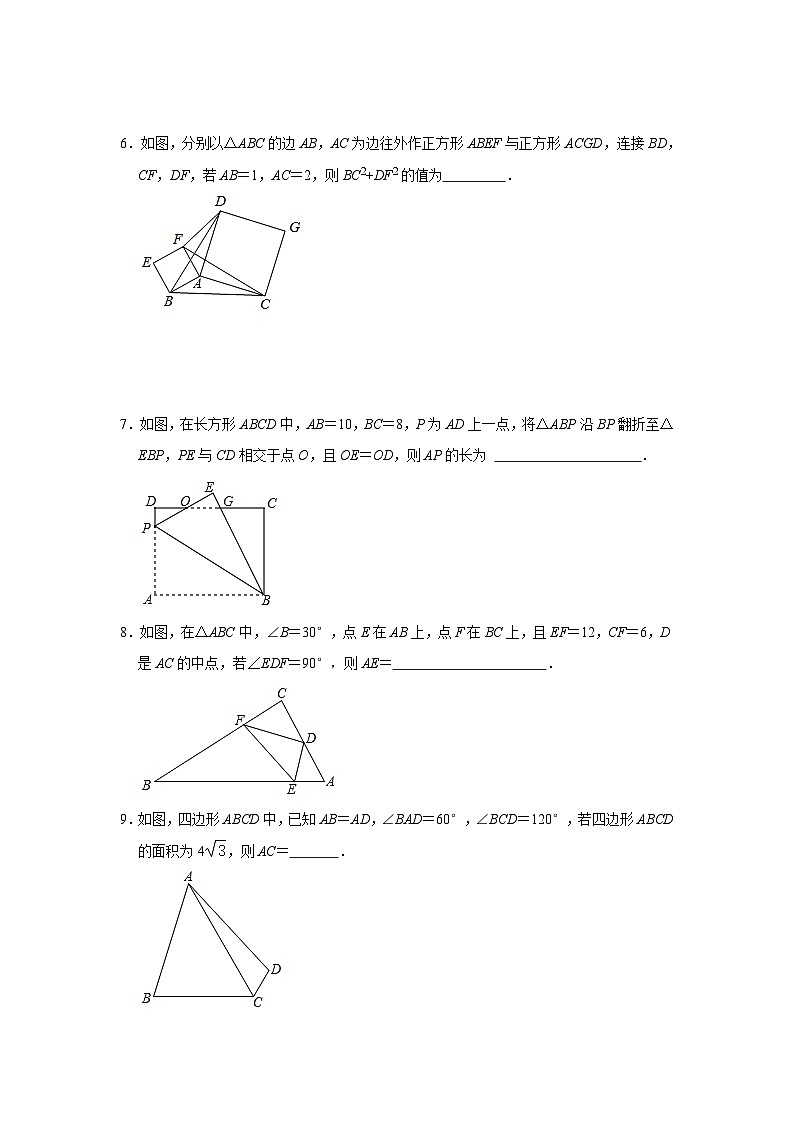
6．如图，分别以△ABC的边AB，AC为边往外作正方形ABEF与正方形ACGD，连接BD，CF，DF，若AB＝1，AC＝2，则BC2+DF2的值为 ．
7．如图，在长方形ABCD中，AB＝10，BC＝8，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，且OE＝OD，则AP的长为 ．
8．如图，在△ABC中，∠B＝30°，点E在AB上，点F在BC上，且EF＝12，CF＝6，D是AC的中点，若∠EDF＝90°，则AE＝ ．
9．如图，四边形ABCD中，已知AB＝AD，∠BAD＝60°，∠BCD＝120°，若四边形ABCD的面积为4，则AC＝ ．
三．解答题（共8小题）
10．在△ABC中，AD是∠BAC的平分线．
（1）如图①，求证：；
（2）如图②，若BD＝CD，求证：AB＝AC；
（3）如图③，若AB＝5，AC＝4，BC＝6．求BD的长．
11．（1）如图1，锐角△ABC中分别以AB、AC为边向外作等腰△ABE和等腰△ACD，使AE＝AB，AD＝AC，∠BAE＝∠CAD，连接BD、CE，试猜想BD与CE的大小关系，并说明理由．
（2）如图2，四边形ABCD中，AB＝7cm，BC＝3cm，∠ABC＝∠ACD＝∠ADC＝45°，求BD的长．
甲同学受到第一问的启发构造了如图所示的一个和△ABD全等的三角形，将BD进行转化再计算，请你准确的叙述辅助线的作法，再计算．
（3）如图3，四边形ABCD中，AB＝BC，∠ABC＝60°，∠ADC＝30°，AD＝6，BD＝10，求CD的长度．
12．（1）问题发现：如图1，△ABC与△CDE均为等腰直角三角形，∠ACB＝∠DCE＝90°，则线段AE、BD的数量关系为 ，AE、BD所在直线的位置关系为 ；
（2）深入探究：在（1）的条件下，若点A，E，D在同一直线上，CM为△DCE中DE边上的高，请判断∠ADB的度数及线段CM，AD，BD之间的数量关系，并说明理由；
（3）解决问题：如图3，已知△ABC中，AB＝7，BC＝3，∠ABC＝45°，以AC为直角边作等腰直角△ACD，∠CAD＝90°，AC＝AD，连接BD，则BD的长为 ．
13．早在古罗马时代，传说亚历山大城有一位精通数学和物理的学者，名叫海伦．一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题．
将军每天从军营A出发，先到河边饮马，然后再去河岸同侧的军营B开会，应该怎样走才能使路程最短？这个问题的答案并不难，据说海伦略加思索就解决了它．从此以后，这个被称为“将军饮马”的问题便流传至今．
大数学家海伦曾用轴对称的方法巧妙地解决了这个问题．
如图2，作B关于直线l的对称点B′，连接AB′与直线l交于点C，点C就是所求的位置．
证明：如图3，在直线l上另取任一点C′，连接AC′，BC′，B′C′，
∵直线l是点B，B′的对称轴，点C，C′在l上，
∴CB＝CB′，C′B＝C′B′，
∴AC+CB＝AC+ ＝ ．
在△AC′B′中，
∵AB′＜AC′+C′B′
∴AC+CB＜AC′+C′B′即AC+CB最小．
本问题实际上是利用轴对称变换的思想，把A，B在直线同侧的问题转化为在直线的两侧，从而可利用“两点之间线段最短”，即“三角形两边之和大于第三边”的问题加以解决（其中C在AB′与l的交点上，即A、C、B′三点共线）．本问题可归纳为“求定直线上一动点与直线外两定点的距离和的最小值”的问题的数学模型．
【简单应用】
（1）如图4，在等边△ABC中，AB＝6，AD⊥BC，E是AC的中点，M是AD上的一点，求EM+MC的最小值
借助上面的模型，由等边三角形的轴对称性可知，B与C关于直线AD对称，连接BM，EM+MC的最小值就是线段 的长度，则EM+MC的最小值是 ；
（2）如图5，在四边形ABCD中，∠BAD＝130°，∠B＝∠D＝90°，在BC，CD上分别找一点M、N当△AMN周长最小时，∠AMN+∠ANM＝ °．
【拓展应用】
如图6，是一个港湾，港湾两岸有A、B两个码头，∠AOB＝30°，OA＝1千米，OB＝2千米，现有一艘货船从码头A出发，根据计划，货船应先停靠OB岸C处装货，再停靠OA岸D处装货，最后到达码头B．怎样安排两岸的装货地点，使货船行驶的水路最短？请画出最短路线并求出最短路程．
14．把两个同样大小的含45°角的三角尺，按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A，且另三个锐角顶点B，C，D在同一直线上，若AB＝，求CD的长．
15．如图，在四边形ABCD中，AD∥BC，DE⊥BC，垂足为点E，连接AC交DE于点F，点G为AF的中点，∠ACD＝2∠ACB．若DG＝3，EC＝1，则DE的长为多少？
16．数学家华罗庚说过“数缺形时少直观，形缺数时难入微；数形结合百般好，隔离分家万事休”．请你利用数形结合的思想解决以下数学问题．
（1）根据图中大正方形面积的两种不同表示方法，可得出代数恒等式 ；
（2）如图，将一张大长方形纸板按图中虚线裁剪成9块，其中有2块是边长为a厘米的大正方形，2块是边长都为b厘米的小正方形，5块是长为a厘米，宽为b厘米的全等的小长方形，且a＞b．
①观察图形，可以发现代数式可以因式分解为 ．
②若阴影部分的面积为20平方厘米，大长方形纸板的周长为24厘米，求图中空白部分的面积．
若a+b＝12（a＞0，b＞0），请你构造合适的图形，直接写出的最小值是 ．
17．在△ABC中，AB＝13，BC＝14．
（1）如图1，AD⊥BC于点D，且BD＝5，则△ABC的面积为 ；
（2）在（1）的条件下，如图2，点H是线段AC上任意一点，分别过点A，C作直线BH的垂线，垂足为E，F，设BH＝x，AE＝m，CF＝n，请用含x的代数式表示m+n，并求m+n的最大值和最小值．
参考答案与试题解析
一．选择题（共3小题）
1．【解答】解：以A为圆心，AB长为半径作圆，延长BA交⊙A于F，连接DF．
∵DC∥AB，
∴＝，
∴DF＝CB＝1，BF＝2+2＝4，
∵FB是⊙A的直径，
∴∠FDB＝90°，
∴BD＝＝．
故选：B．
2．【解答】解：设BD＝x，则CD＝14﹣x，在Rt△ABD中，AD2+x2＝132，
在Rt△ADC中，AD2＝152﹣（14﹣x）2，
∴132﹣x2＝152﹣（14﹣x）2，
132﹣x2＝152﹣196+28x﹣x2，
解得x＝9，
∴CD＝5，
在Rt△ACD中，AD＝＝12，
∴△ABC的面积＝×BC•AD＝×14×12＝84，
故选：C．
3．【解答】解：∵S△ABC＝AB•CD＝AC•BC，AB＝13，CD＝6，
∴AC•BC＝13×6＝78，
∵△ABC为直角三角形，
∴根据勾股定理得：AB2＝AC2+BC2＝169，
∴（AC+BC）2＝AC2+2AC•BC+BC2＝169+156＝325，
则AC+BC＝＝5．
故选：B．
二．填空题（共6小题）
4．【解答】解：如图，过点D作DE⊥AB于E，
∵AD平分∠BAC，
∴点D到AC的距离也等于DE，
∴S△ABC＝×3•DE+×4•DE＝×3×4，
解得DE＝，
∵AD平分∠BAC，∠BAC＝90°，
∴∠DAE＝45°，
∴△ADE是等腰直角三角形，
∴AE＝DE＝，
∴BE＝3﹣＝，
在Rt△BDE中，BD＝＝＝．
故答案为：．
5．【解答】解：设两条直角边分别为a、b，斜边为c，
由题意得，a+b+c＝+2，
∵c＝2，
∴a+b＝，
则（a+b）2＝6，即a2+2ab+b2＝6，
由勾股定理得，a2+b2＝c2＝4，
∴2ab＝6﹣4＝2，
∴这个三角形的面积＝ab＝0.5，
故答案为：0.5．
6．【解答】解：连接BF、CD，BD与CF相交于O点，CF交AD于P，如图，
∵四边形ABEF和四边形ACGD为正方形，
∴AB＝AF，AC＝AD，∠BAF＝∠CAD＝90°，BF＝AB＝，CD＝AC＝2，
∵∠BAF＝∠CAD，
∴∠BAF+∠DAF＝∠CAD+∠DAF，
即∠BAD＝∠FAC，
在△ABD和△AFC中，
，
∴△ABD≌△AFC（SAS），
∴∠ADB＝∠ACF，
∵∠PDO+∠POD+∠DPO＝∠PCA+∠PAC+∠APC，
而∠DPO＝∠APC，
∴∠POD＝∠PAC＝90°，
在Rt△CDO中，OD2+OC2＝CD2，
在Rt△BOF中，OB2+OF2＝BF2，
在Rt△CBO中，OB2+OC2＝BC2，
在Rt△DOF中，OD2+OF2＝DF2，
∴BC2+DF2＝CD2+BF2＝（2）2+（）2＝10．
故答案为10．
7．【解答】解：设CD与BE交于点G，
∵四边形ABCD是矩形，
∴∠D＝∠A＝∠C＝90°，AD＝BC＝8，CD＝AB＝10，
由折叠的性质可知△ABP≌△EBP，
∴EP＝AP，∠E＝∠A＝90°，BE＝AB＝10，
在△ODP和△OEG中，
，
∴△ODP≌△OEG（ASA），
∴OP＝OG，PD＝GE，
∴DG＝EP，
设AP＝EP＝x，则PD＝GE＝8﹣x，DG＝x，
∴CG＝10﹣x，BG＝10﹣（8﹣x）＝2+x，
根据勾股定理得：BC2+CG2＝BG2，
即82+（10﹣x）2＝（x+2）2，
解得：x＝，
∴AP＝，
故答案为：．
8．【解答】解：延长FD至点H，使得FD＝DH，连接AH，过H作HG⊥AB，交BA的延长线于点G，
∵D是AC的中点，
∴DA＝DC，
在△DAH和△DCF中，
，
∴△DAH≌△DCF（SAS），
∴AH＝CF＝6，∠DAH＝∠C，
∴AH∥BC，
∴∠HAG＝∠B＝30°，
∴HG＝AH＝3，AG＝AH•cs30°＝3，
∵DE⊥DF，DH＝DF，
∴EH＝EF＝12，
∴EG＝＝＝3，
∴AE＝EG﹣AG＝3﹣3．
故答案为：3﹣3．
9．【解答】将△ACD绕点A顺时针旋转60°，得到△ABE．
∵四边形内角和360°，
∴∠D+∠ABC＝180°．
∴∠ABE+∠ABC＝180°，
∴E、B、C三点共线．
根据旋转性质可知∠EAC＝60度，AE＝AC，
∴△AEC是等边三角形．
四边形ABCD面积等于△AEC面积，
等边△AEC面积＝，解得AC＝4．
故答案为4．
三．解答题（共8小题）
10．【解答】
解：（1）如图①，证明：作DE⊥AB于E，DF⊥AC于F，∵AD是∠BAC的平分线，
∴DE＝DF
∴；
（2）∵BD＝CD，∴S△ABD＝S△ACD
由（1）的结论，
∴，
∴AB＝AC；
（3）如图③，过A作AE⊥BC，垂足为E，
∵，
∴
由（1）的结论，
∴，
∴BD＝，DC＝．
11．【解答】解：（1）BD＝CE．
理由是：∵∠BAE＝∠CAD，
∴∠BAE+∠BAC＝∠CAD+∠BAC，
即∠EAC＝∠BAD，
在△EAC和△BAD中，
，
∴△EAC≌△BAD（SAS），
∴BD＝CE；
（2）如图2，在△ABC的外部，以A为直角顶点作等腰直角△BAE，使∠BAE＝90°，AE＝AB，连接EA、EB、EC．
∵∠ACD＝∠ADC＝45°，
∴AC＝AD，∠CAD＝90°，
∴∠BAE+∠BAC＝∠CAD+∠BAC，
即∠EAC＝∠BAD，
在△EAC和△BAD中，
，
∴△EAC≌△BAD（SAS），
∴BD＝CE．
∵AE＝AB＝7，
∴BE＝＝＝7，∠ABE＝∠AEB＝45°，
又∵∠ABC＝45°，
∴∠ABC+∠ABE＝45°+45°＝90°，
∴EC＝＝＝，
∴BD＝CE＝，
（3）∵AB＝BC，∠ABC＝60°，
∴△ABC是等边三角形，
如图3，把△ACD绕点C逆时针旋转60°得到△BCE，连接DE，
则BE＝AD＝6，△CDE是等边三角形，
∴DE＝CD，∠CED＝60°，
∵∠ADC＝30°，
∴∠BED＝30°+60°＝90°，
在Rt△BDE中，DE＝＝＝8，
∴CD＝DE＝8．
12．【解答】解：（1）结论：AE＝BD，AE⊥BD．
理由：如图1中，延长AE交BD于点H，AH交BC于点O．
∵△ACB和△DCE均为等腰直角三角形，
∠ACB＝∠DCE＝90°，
∴AC＝BC，CD＝CE，
∴∠ACE＝∠BCD，
∴△ACE≌△BCD（SAS），
∴AE＝BD，∠CAE＝∠CBD，
∵∠CAE+∠AOC＝90°，∠AOC＝∠BOH，
∴∠BOH+∠CBD＝90°
∴∠AHB＝90°，
∴AE⊥BD．
故答案为AE＝BD，AE⊥BD．
（2）结论：AD＝2CM+BD，
理由：如图2中，
∵△ACB和△DCE均为等腰直角三角形，
∠ACB＝∠DCE＝90°，
∴AC＝BC，CD＝CE，
∴∠ACE＝∠BCD，
∴△ACE≌△BCD（SAS），
∴AE＝BD，∠BDC＝∠AEC＝135°．
∴∠ADB＝∠BDC﹣∠CDE＝135°﹣45°＝90°；
在等腰直角三角形DCE中，CM为斜边DE上的高，
∴CM＝DM＝ME，
∴DE＝2CM．
∴AD＝DE+AE＝2CM+BD．
（3）情形1：如图3﹣1中，在△ABC的外部，以A为直角顶点作等腰直角△BAE，使∠BAE＝90°，AE＝AB，连接EA、EB、EC．
∵∠ACD＝∠ADC＝45°，
∴AC＝AD，∠CAD＝90°，
∴∠BAE+∠BAC＝∠CAD+∠BAC，即∠EAC＝∠BAD，
∴△EAC≌△BAD（SAS），
∴BD＝CE．
∵AE＝AB＝7，
∴BE＝＝7，∠ABE＝∠AEB＝45°，
又∵∠ABC＝45°，
∴∠ABC+∠ABE＝45°+45°＝90°，
∴EC＝＝＝，
∴BD＝CE＝．
情形2：如图3﹣2中，作AE⊥AB交BC的延长线于E，则△ABE是等腰直角三角形，
同法可证：△EAC≌△BAD（SAS），
∴BD＝CE，
∵AB＝AE＝7，
∴BE＝7，
∴EC＝BE＝CB＝7﹣3，
综上所述，BD的长为或7﹣3．
故答案为或7﹣3．
13．【解答】解：AC+CB＝AC+CB′＝AB′，
故答案为：CB′；AB′；
【简单应用】（1）由等边三角形的轴对称性可知，B与C关于直线AD对称，连接BM，
EM+MC的最小值就是线段BE的长度，
BE＝＝3，
则EM+MC的最小值是3，
故答案为：BE；3；
（2）如图5，作A关于BC和CD的对称点A′，A″，连接A′A″，交BC于M，交CD于N，
则A′A″即为△AMN的周长最小值，
∵∠DAB＝130°，
∴∠AA′M+∠A″＝50°，
∵∠MA′A＝∠MAA′，∠NAD＝∠A″，
且∠MA′A+∠MAA′＝∠AMN，∠NAD+∠A″＝∠ANM，
∴∠AMN+∠ANM＝∠MA′A+∠MAA′+∠NAD+∠A″＝2（∠AA′M+∠A″）＝2×50°＝100°，
故答案为：100；
【拓展应用】如图6，分别作点A关于OB的对称点A′，点B关于OA的对称点B′，连接A′B′，交OB于C，交OA于D，
则C、D为两岸的装货地点，A′B′是货船行驶的水路最短路程，
由轴对称的性质可知，OA′＝OA＝1，OB′＝OB＝2，∠BOA′＝∠AOB＝30°，∠AOB′＝∠AOB＝30°，
∴∠A′OB′＝90°，
∴A′B′＝＝，
答：货船行驶的水路最短路程为千米．
14．【解答】解：如图，过点A作AF⊥BC于F，
在Rt△ABC中，∠B＝45°，
∴BC＝AB＝2，BF＝AF＝AB＝1，
∵两个同样大小的含45°角的三角尺，
∴AD＝BC＝2，
在Rt△ADF中，根据勾股定理得，DF＝＝，
∴CD＝BF+DF﹣BC＝1+﹣2＝﹣1．
15．【解答】解：∵AD∥BC，DE⊥BC，
∴∠DAG＝∠ACB，DE⊥AD，
∴∠ADF＝90°，
∵AG＝GF，
∴DG＝AG＝GF，
∴∠GAD＝∠GDA，
∴∠DGC＝∠GAD+∠GDA＝2∠GAD，
∵∠DCG＝2∠ACB，
∴∠DGC＝∠DCG，
∴DG＝DC＝3，
在Rt△DEC中，∵∠DEC＝90°，DC＝3，EC＝1，
∴DE＝＝2．
16．【解答】解：（1）由图知，大正方形的边长为（a+b+c），所以大正方形的面积为（a+b+c）2，
由各部分面积和可得大正方形的面积为：a2+b2+c2+2ab+2bc+2ac，
∴可得代数恒等式：（a+b+c）2＝a2+b2+c2+2ab+2bc+2ac，
故答案为：（a+b+c）2＝a2+b2+c2+2ab+2bc+2ac；
（2）①由各部分和可得大矩形的面积为：2a2+2b2+5ab，
由图知，在矩形的长为（2a+b），宽为（a+2b），则大矩形的面积也可表示为：（2a+b）（a+2b），
∴由该图可得 因式分解为：2a2+2b2+5ab＝（2a+b）（a+2b），
故答案为：2a2+2b2+5ab＝（2a+b）（a+2b）；
②∵阴影部分的面积为20平方厘米，大长方形纸板的周长为24厘米，
∴2a2+2b2＝20，2（2a+b+a+2b）＝24，
∴a2+b2＝10，a+b＝4，
∵（a+b）2＝a2+b2+2ab，
∴16＝10+2ab，
∴ab＝3，
∴图中空白部分的面积＝（2a+b）（a+2b）﹣2（a2+b2）＝5ab＝5×3＝15；
（3）画线段AB＝a+b＝12，再过分别过A、B两点，在直线AB两旁分别作AM⊥AB，BN⊥AB，并分别在AM、BN上截取AC＝2，BD＝3，连接CD，
设AH＝a，则BH＝12﹣a＝b，连接AH，DH，
由勾股定理得CH＝，DH＝，
∴＝CH+DH≥CD，
当C、H、D三点依次在同一直线上时，＝CH+DH＝CD的值最小，
过点C作CF⊥DB，与DB的延长线交于点F，则MF＝AB＝12，BF＝AC＝2，
∴DF＝DB+BF＝3+2＝5，
由勾股定理得CD＝，
∴的最小值是13．
故答案为：13．
17．【解答】解：（1）在Rt△ABD中，AB＝13，BD＝5，
∴AD＝＝＝12．
∵BC＝14，
∴＝＝84．
故答案为：84．
（2）∵SABC＝SABH+S△BHC，
∴．
∴xm+xn＝168．
∴m+n＝
∵AD＝12，DC＝14﹣5＝9，
∴AC＝＝15．
∵m+n与x成反比，
∴当BH⊥AC时，m+n有最大值．
∴（m+n）BH＝AC•BH．
∴m+n＝AC＝15．
∵m+n与x成反比，
∴当BH值最大时，m+n有最小值．
∴当点H与点C重合时m+n有最小值．
∴m+n＝，
∴m+n＝12．
∴m+n的最大值为15，最小值为12．：试题解析著作权属菁优网所有，未经书面同意，不得