




北京市丰台区2024-2025学年高一上学期11月期中数学试题
展开
这是一份北京市丰台区2024-2025学年高一上学期11月期中数学试题,文件包含丰台区2024-2025学年度第一学期期中练习高一数学答案docx、丰台区2024-2025学年度第一学期期中练习高一数学试卷docx等2份试卷配套教学资源,其中试卷共16页, 欢迎下载使用。
第I卷(选择题 共40分)
一、选择题共10小题,每小题4分。在每小题给出的四个选项中,选出符合题目要求的一项。
(1)已知集合,,则
(A) (B) (C) (D)
(2)命题“,”的否定是
(A), (B),
(C), (D),
(3)下列函数中,在区间上单调递减的是
(A) (B)
(C) (D)
(4)已知函数的定义域和值域均为,则的图象可能为
(A) (B)
(C) (D)
(5)已知关于的一元二次不等式的解集为,则的值为
(A) (B) (C) (D)
(6)“”是“”的
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
(7)已知函数,,对,用表示,中的最小者,记为,则当取得最大值时的值为
(A) (B) (C) (D)
(8)已知是定义域为的偶函数,且在区间上单调递增,则与的大小关系为
(A) (B)
(C) (D)不确定
(9)2024年7月15日至18日,党的二十届三中全会在北京隆重举行,全会审议并通过了《中共中央关于进一步全面深化改革、推进中国式现代化的决定》(以下简称《决定》),《决定》中指出要完善基本公共服务制度体系,加强普惠性、基础性、兜底性民生建设,解决好人民最关心最直接最现实的利益问题,不断满足人民对美好生活的向往.居民用水作为民生建设的重要内容,愈发引起社会关注,现已知某城市对居民生活用水实行“阶梯水价”.计费方法如下表:
若某户居民希望本月缴纳的水费不超过51.4元,则此户居民本月用水最多为
(A)19m³ (B)20m³ (C)21m³ (D)22m³
(10)已知定义域为的函数满足为偶函数.当时,,且当时,.对,都有,则的最小值为
(A) (B) (C) (D)
第Ⅱ卷(非选择题 共110分)
二、填空题共5小题,每小题5分,共25分。
(11)函数的定义域为 .
(12)设集合,若,则实数的值为 .
(13)能够说明“若,则”是假命题的一组实数的值依次为 .
(14)设函数若,则的值域是 ;若的值域是,则实数的取值范围是 .
(15)已知的定义域为,对,,若同时满足以下两个条件:
(i);
(ii),
则称具有“丰彩”性质.现给出以下定义域均为的四个函数:
①; ②;
③; ④.
其中所有具有“丰彩”性质的函数序号是 .
三、解答题共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
(16)(本小题14分)
已知集合,.
(Ⅰ)若,求,;
(Ⅱ)若,求实数的取值范围.
(17)(本小题13分)
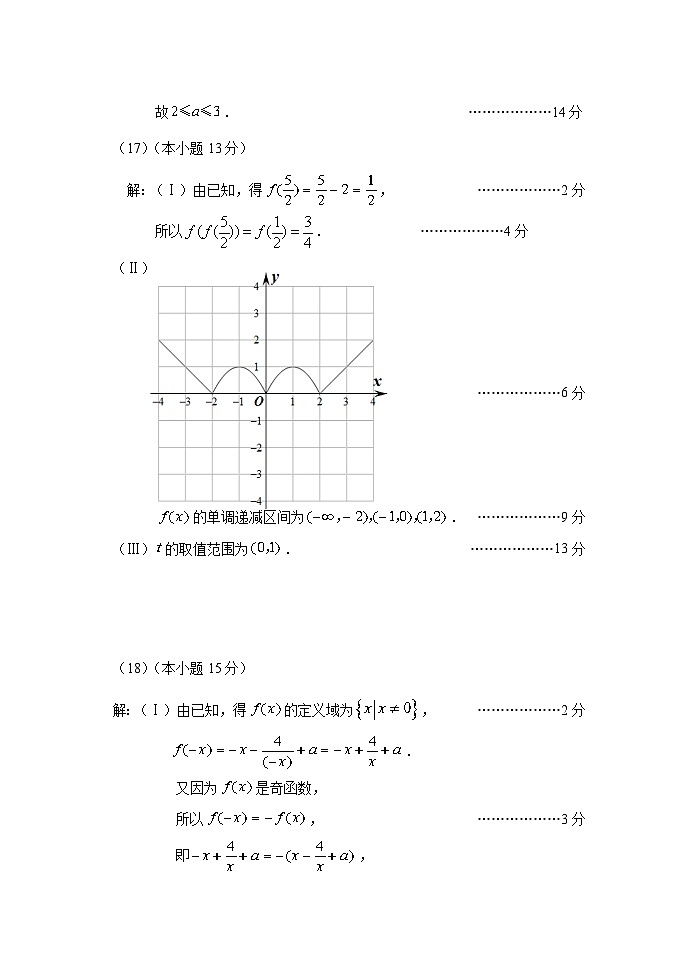
已知是定义域为的偶函数,当时,
(Ⅰ)求的值;
(Ⅱ)的部分图象如下图,请将的图象补充完整,并写出的单调递减区间;
(Ⅲ)若关于的方程恰有6个实数根,则实数的取值范围是________.
(18)(本小题15分)
设函数,.
(Ⅰ)若为奇函数,求实数的值;
(Ⅱ)根据定义证明在区间上单调递增;
(Ⅲ)若对,,使得,求实数的取值范围.
(19)(本小题15分)
设函数.
(Ⅰ)若______(从条件①、条件②、条件③这三个条件中选择一个作为已知),
求实数的值,并以此时的图象与坐标轴的交点为三角形的顶点,求该三角形的面积;
条件①:关于的方程有两个实数根,且;
条件②:,都有;
条件③:的最小值为,且.
注:如果选择多个条件分别解答,按第一个解答计分.
(Ⅱ)求关于的不等式的解集.
(20)(本小题14分)
某公司计划生产一类电子设备,该电子设备每月产量不超过150台,每台售价为40万元. 每月生产该电子设备的成本由固定成本和可变成本两部分组成,固定成本为20万元,每月生产台时需要投入的可变成本为(单位:万元),每月的利润为(单位:万元),其中利润是收入与成本之差.当每月产量不超过40台时,;当每月产量超过40台时,.假设该公司每月生产的电子设备都能够售罄.
(Ⅰ)求关于的函数解析式;
(Ⅱ)如果你是该公司的决策者,分析每月生产多少台电子设备可以使月利润最大?最大利润是多少?
(21)(本小题14分)
给定正整数,设集合,对,,,两数中至少有一个数属于,则称集合具有性质.
(Ⅰ)设集合,,请直接写出,是否具有性质;
(Ⅱ)若集合具有性质,求的值;
(Ⅲ)若具有性质的集合恰有6个元素,且,求集合.
(考生务必将答案写在答题卡上,在试卷上作答无效)每户每月用水量
水价
不超过15m³的部分
2.07元/m³
超过15m³但不超过21.67m³的部分
4.07元/m³
超过21.67m³的部分
6.07元/m³
相关试卷
这是一份北京市丰台区2023-2024学年高一上学期期末数学试题(Word版附答案),共10页。试卷主要包含了01,函数,则,荀子《劝学》中说等内容,欢迎下载使用。
这是一份2023-2024学年北京市丰台区高一上学期期中练习数学试题(A)含答案,共15页。试卷主要包含了单选题,填空题,解答题,作图题,证明题,问答题,应用题等内容,欢迎下载使用。
这是一份2023-2024学年北京市丰台区高二上学期期中练习数学试题(B)含答案,共18页。试卷主要包含了单选题,填空题,问答题,证明题,应用题等内容,欢迎下载使用。








