

福建省南平市浦城县2022-2023学年高一下学期期末冲刺卷(三)数学试卷(解析版)
展开
这是一份福建省南平市浦城县2022-2023学年高一下学期期末冲刺卷(三)数学试卷(解析版),共16页。试卷主要包含了单项选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。
一、单项选择题(本大题共8小题,每小题5分,共40分.)
1. 设,,则在复平面内对应的点位于( )
A. 第一象限B. 第二象限
C. 第三象限D. 第四象限
【答案】C
【解析】,
在复平面内对应的点为,
所以在复平面内对应的点位于第三象限.
故选:C.
2. 如图,设O是正六边形ABCDEF的中心,在向量,,,,,,,,,,中,与共线的向量有( )
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】在向量,,,,,,,,,,
中与共线的向量有:向量,,.
故选:C.
3. 已知正四棱柱ABCD-A1B1C1D1中,AB=2,CC1=,E为CC1的中点,则直线AC1与平面BED的距离为( )
A. 2B. C. D. 1
【答案】D
【解析】因为线面平行,所求求线面距可以转化为求点到面的距离,选用等体积法,
平面,到平面的距离等于到平面的距离,
由题计算得,
在中,,
边上的高,所以,
所以,利用等体积法,
得:,解得:.
故选:D.
4. 在中,已知,,的外接圆半径为1,则( )
A. B. C. D. 6
【答案】C
【解析】已知A=,得sinA=,
∵b=1,R=1,根据正弦定理,得,sinB=,
∵,易知B为锐角,∴B=,∴C=,
根据三角形的面积公式,S△ABC=.
故选:C.
5. 已知数据的平均数为,方差为,则,,…,的平均数和方差分别为( )
A. 和B. 和
C. 和D. 和
【答案】B
【解析】因为数据的平均数为,方差为,
所以,,…,的平均数和方差分别为和.
故选:B.
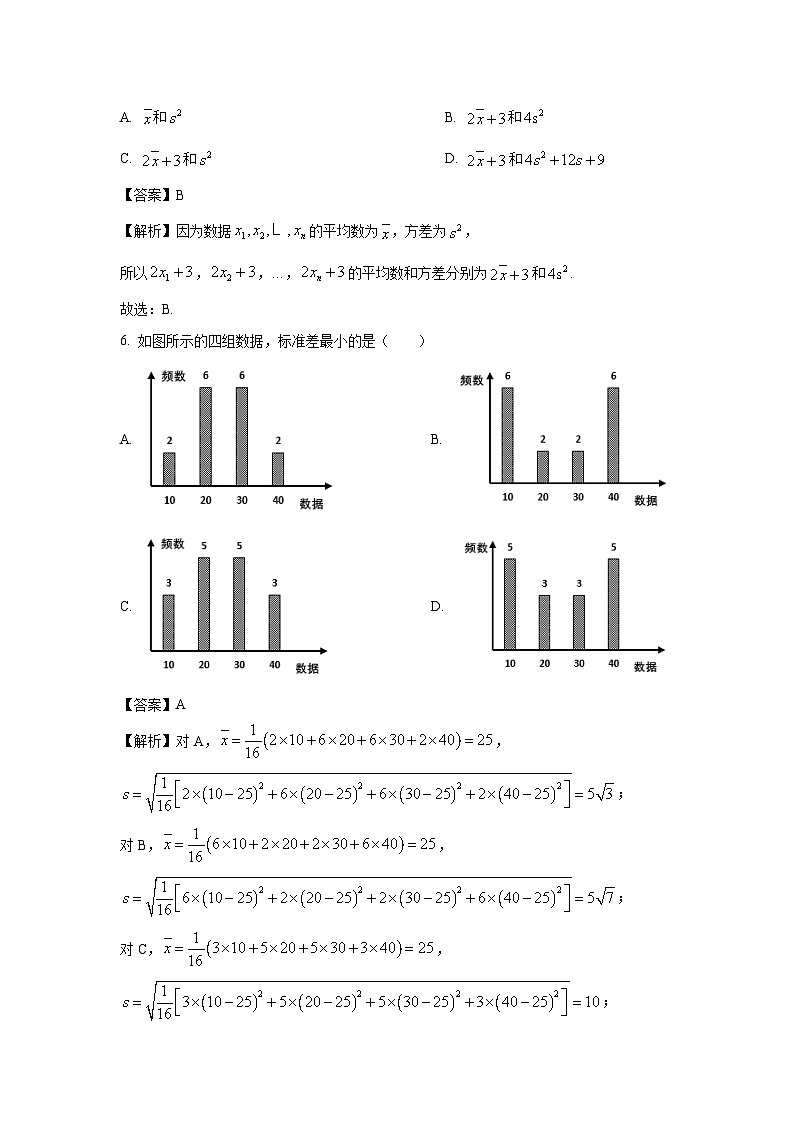
6. 如图所示的四组数据,标准差最小的是( )
A. B.
C. D.
【答案】A
【解析】对A,,
;
对B,,
;
对C,,
;
对D,,
;
所以标准差最小的是A.
故选:A.
7. 已知正四棱柱(即底面是正方形的直棱柱)的底面边长为,侧面的对角线长是,则这个正四棱柱的表面积为( )
A. B. C. D.
【答案】A
【解析】由题意侧棱长为,
所以表面积为:.
故选:A.
8. 海伦公式是利用三角形的三条边的边长直接求三角形面积S的公式,表达式为:;它的特点是形式漂亮,便于记忆.中国宋代的数学家秦九韶在1247年独立提出了“三斜求积术”,虽然它与海伦公式形式上有所不同,但它与海伦公式完全等价,因此海伦公式又译作海伦-秦九韶公式.现在有周长为的满足,则用以上给出的公式求得的面积为( )
A. B.
C. D. 12
【答案】C
【解析】在中,因为,
由正弦定理可得:,
设,,,且,
∴,解得,
即,,,且,
∴
.
故选:C.
二、多项选择题(本大题共4小题,每小题5分,共20分.全部选对的得5分,部分选对的得2分,有选错的得0分.)
9. 小明与小华两人玩游戏,则下列游戏公平的有( )
A. 抛掷一枚骰子,向上的点数为奇数,小明获胜,向上的点数为偶数,小华获胜
B. 同时抛掷两枚硬币,恰有一枚正面向上,小明获胜,两枚都正面向上,小华获胜
C. 从一副不含大小王的扑克牌中抽一张,扑克牌是红色,小明获胜,扑克牌是黑色,小华获胜
D. 小明、小华两人各写一个数字6或8,如果两人写的数字相同,小明获胜,否则小华获胜
【答案】ACD
【解析】对于A,抛掷一枚骰子,向上的点数为奇数和向上的点数为偶数是等可能的,所以游戏公平
对于B,恰有一枚正面向上包括正,反反,正两种情况,
而两枚都正面向上仅有正,正一种情况,所以游戏不公平
对于C,从一副不含大小王的扑克牌中抽一张,扑克牌是红色和扑克牌是黑色是等可能的,
所以游戏公平
对于D,小明、小华两人各写一个数字6或8,一共四种情况:(6,6),(6,8),(8,6),
(8,8);两人写的数字相同和两人写的数字不同是等可能的,所以游戏公平.
故选:ACD.
10. 在中,a,b,c分别为角A,B,C的对边,已知,,且,则( )
A. B.
C. D.
【答案】AD
【解析】,由正弦定理可得,
整理可得,
所以,
为三角形内角,,
∴,∵,,故A正确,B错误;
∵,,
,解得,
由余弦定理,得,
解得或(舍去),故D正确,C错误.
故选:AD.
11. 如图所示,在正方体中,为的中点,直线交平面于点,则下列结论正确的是( )
A. ,,三点共线B. ,,,四点共面
C. ,,,四点共面D. ,,,四点共面
【答案】ABC
【解析】在正方体中,为的中点,直线交平面于点,
在选项中,直线交平面于点,
平面,直线,又平面,平面,
为的中点,平面,底面为正方形,所以为的中点,
平面,且平面,
又平面,且平面,,,三点共线,故选项正确;
在选项中,,,三点共线,,,,四点共面,故正确;
在选项中,,,三点共线,,,,四点共面,故正确;
在选项中,直线,,
,,,四点不共面,故错误.
故选:ABC.
12. 对于三角形ABC,有如下判断,其中正确的判断是( )
A. 若sin2A+sin2B<sin2C,则三角形ABC是钝角三角形
B. 若A>B,则sin A>sin B
C. 若a=8,c=10,B=60°,则符合条件的三角形ABC有两个
D. 若三角形ABC为斜三角形,则
【答案】ABD
【解析】对于A,因为sin2A+sin2B<sin2C,所以由正弦定理得,
所以,所以为钝角,所以三角形ABC是钝角三角形,
所以A正确;
对于B,因为A>B,所以,所以由正弦定理得sin A>sin B,所以B正确;
对于C,由余弦定理得,,
所以,所以符合条件的三角形ABC有一个,所以C错误;
对于D,因为,
所以
因为,
所以,
所以,所以D正确.
故选:ABD.
三、填空题(本大题共4小题,每小题5分,共20分.)
13. 已知向量,,.若与共线,则在方向上的投影为________.
【答案】
【解析】因为,,
所以;
因为与共线,,
所以,解得;
所以在方向上的投影为.
故答案为:.
14. 已知复数满足条件,那么的最大值为______.
【答案】4
【解析】因为,所以复数对应的点在单位圆上,
表示复数对应的点与复数对应的点之间的距离,
而,
所以的最大值为.
故答案为:4.
15. 在山顶铁塔上处测得地面上一点的俯角,在塔底处测得点的俯角,已知铁塔部分高米,山高_______.
【答案】米
【解析】由,易得,,
设,则,
,
,.
故答案为:米.
16. 如图,点E是正方体的棱的中点,点在线段上运动,则下列结论正确的有__________.
①直线与直线始终是异面直线;
②存在点,使得;
③四面体的体积为定值;
④当时,平面平面.
【答案】②③④.
【解析】对于①:连接交于点,当点在点时直线与直线相交,
故①不正确,
以为坐标原点,建立如图所示空间直角坐标系,设正方体的边长为,则,
,,,,,,
对于②:,假设存在点,使得,
,,
所以,解得,所以当时,
故②正确;
对于③:连接、交于点,因为点E是棱的中点,此时,
故线段到平面的距离为定值,所以四面体的体积为定值,故③正确;
对于④:当时,,,,
设平面的法向量为,由,令,
可得,,可得,设平面的法向量为,
,由解得:,
令可得,所以,因为,,
所以平面平面,故④正确.
故答案为:②③④.
四、解答题(本大题共6小题,17题10分,18-22题每题12分,共70分.)
17. 实数取什么值时,复数.
(1)与复数相等;
(2)与复数互为共轭复数;
(3)对应的点在轴上方.
解:(1)根据复数相等的充要条件得,解得m=-1.
(2)根据共轭复数的定义得,解得m=1.
(3)根据复数z的对应点在x轴的上方可得m2-2m-15>0,解得m5.
18. 已知向量.
(1)若,求证:;
(2)若向量共线,求.
解:(1)当时,,
又,.
(2)因为向量共线,,即,
当,则与矛盾,故舍去;
当时,由得:,
又
.
另解:由,得,所以.
19. 为了落实习主席提出“绿水青山就是金山银山”的环境治理要求,某市政府积极鼓励居民节约用水.计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准(吨),一位居民的月用水量不超过的部分按平价收费,超出的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年200位居民每人的月均用水量(单位:吨),将数据按照[0,1),[1,2),…,[8,9)分成9组,制成了如图所示的频率分布直方图,其中.
(1)求直方图中的值,并由频率分布直方图估计该市居民用水的平均数(每组数据用该组区间中点值作为代表);
(2)设该市有40万居民,估计全市居民中月均用水量不低于2吨的人数,并说明理由;
(3)若该市政府希望使85%的居民每月的用水量不超过标准(吨),估计的值,并说明理由.
解:(1)由频率分布直方图可得,
又,则,,
该市居民用水的平均数估计为:
.
(2)由频率分布直方图可得,
月均用水量不超过2吨的频率为:,
则月均用水量不低于2吨的频率为:,
所以全市40万居民中月均用水量不低于2吨的人数为:(万).
(3)由频率分布直方图知月均用水量不超过6吨的频率为:0.88,
月均用水量不超过5吨的频率为0.73,
则85%的居民每月的用水量不超过的标准(吨),,
,解得,
即标准为5.8吨.
20. 如图,在三棱锥中,平面ABC,底面ABC是直角三角形,,O是棱的中点,G是的重心,D是PA的中点.
(1)求证:平面;
(2)求证:平面;
解:(1)证明:平面ABC,且平面ABC,,
底面ABC是直角三角形且,,
又平面PAB,平面PAB,,
平面.
(2)证明:连结并延长交于点,连结,,
是的重心,为边上的中线,为边上的中点,
又有为边上的中点,,
平面PBC,平面PBC,
同理可得平面PBC,
又平面DOE,平面DOE,,
平面DOE平面PBC,
又有平面DOE,平面.
21. 如图,在圆内接中,内角A,B,C所对的边分别为a,b,c,满足.
(1)求B;
(2)若点D是劣弧AC上一点,AB=2,BC=3,AD=1,求四边形ABCD的面积
解:(1)由正弦定理得,
得,
因为,所以,即.
(2)在中AB=2,BC=3,,,
解得,
在中,,A,B,C,D在圆上,
因为,所以,
所以,
解得或(舍去),
所以四边形ABCD的面积.
22. 如图,棱柱中,底面是平行四边形,侧棱底面,过的截面与上底面交于,且点在棱上,点在棱上,且,,.
(1)求证:;
(2)若二面角的平面角的余弦值为,求侧棱的长.
解:(1)在棱柱中,面,面,
面面,由线面平行的性质定理有,
又,故.
(2)证明:在底面中,,,,
, ,,
又因侧棱底面,则底面,
面,,
又,面,
过点作于,连接,则是二面角的平面角,
,,
则,故,
,,
设,则,
,,
故,故.
相关试卷
这是一份2022-2023学年福建省南平市浦城县高二(上)期中数学试卷-普通用卷 (1),共15页。试卷主要包含了抛物线y=43x2的焦点坐标为,已知F1,F2分别为双曲线C等内容,欢迎下载使用。
这是一份2022-2023学年福建省南平市浦城县高二(上)期中数学试卷-普通用卷,共15页。试卷主要包含了抛物线y=43x2的焦点坐标为,已知F1,F2分别为双曲线C等内容,欢迎下载使用。
这是一份福建省南平市浦城县2022-2023学年高一数学下学期期末冲刺试卷(二)(Word版附解析),共18页。试卷主要包含了单项选择题.,多项选择题.,解答题.等内容,欢迎下载使用。










