+广东省湛江市雷州市2023-2024学年八年级上学期第一次月考数学试卷+

这是一份+广东省湛江市雷州市2023-2024学年八年级上学期第一次月考数学试卷+，共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

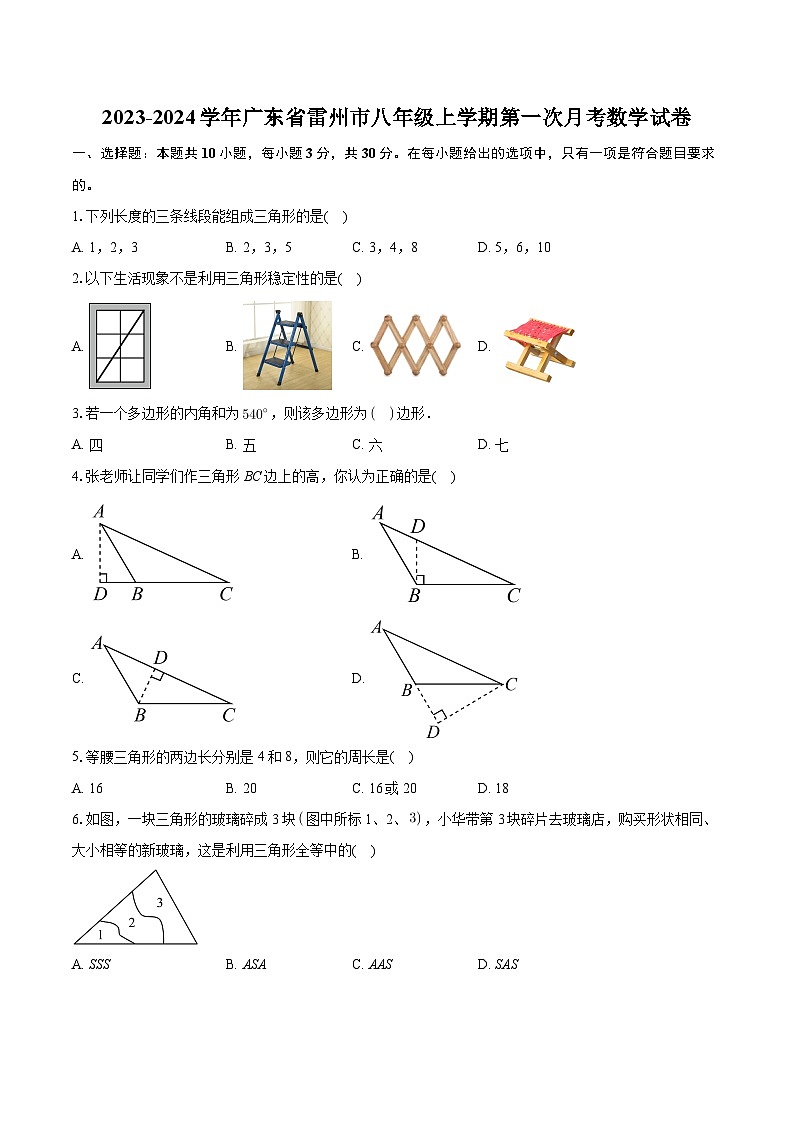
1.下列长度的三条线段能组成三角形的是( )
A. 1，2，3B. 2，3，5C. 3，4，8D. 5，6，10
2.以下生活现象不是利用三角形稳定性的是( )
A. B. C. D.
3.若一个多边形的内角和为，则该多边形为边形．
A. 四B. 五C. 六D. 七
4.张老师让同学们作三角形BC边上的高，你认为正确的是( )
A. B.
C. D.
5.等腰三角形的两边长分别是4和8，则它的周长是( )
A. 16B. 20C. 16或20D. 18
6.如图，一块三角形的玻璃碎成3块图中所标1、2、，小华带第3块碎片去玻璃店，购买形状相同、大小相等的新玻璃，这是利用三角形全等中的( )
A. SSSB. ASAC. AASD. SAS
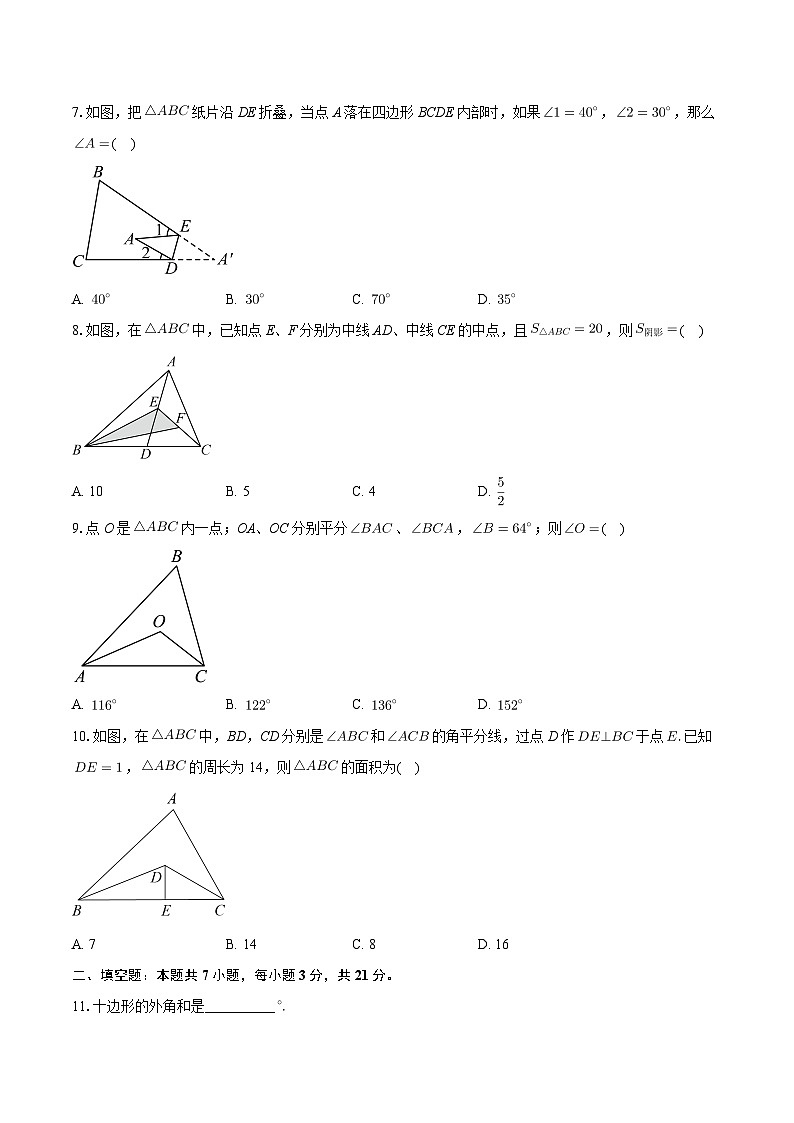
7.如图，把纸片沿DE折叠，当点A落在四边形BCDE内部时，如果，，那么( )
A. B. C. D.
8.如图，在中，已知点E、F分别为中线AD、中线CE的中点，且，则( )
A. 10B. 5C. 4D.
9.点O是内一点；OA、OC分别平分、，；则( )
A. B. C. D.
10.如图，在中，BD，CD分别是和的角平分线，过点D作于点已知，的周长为14，则的面积为( )
A. 7B. 14C. 8D. 16
二、填空题：本题共7小题，每小题3分，共21分。
11.十边形的外角和是__________
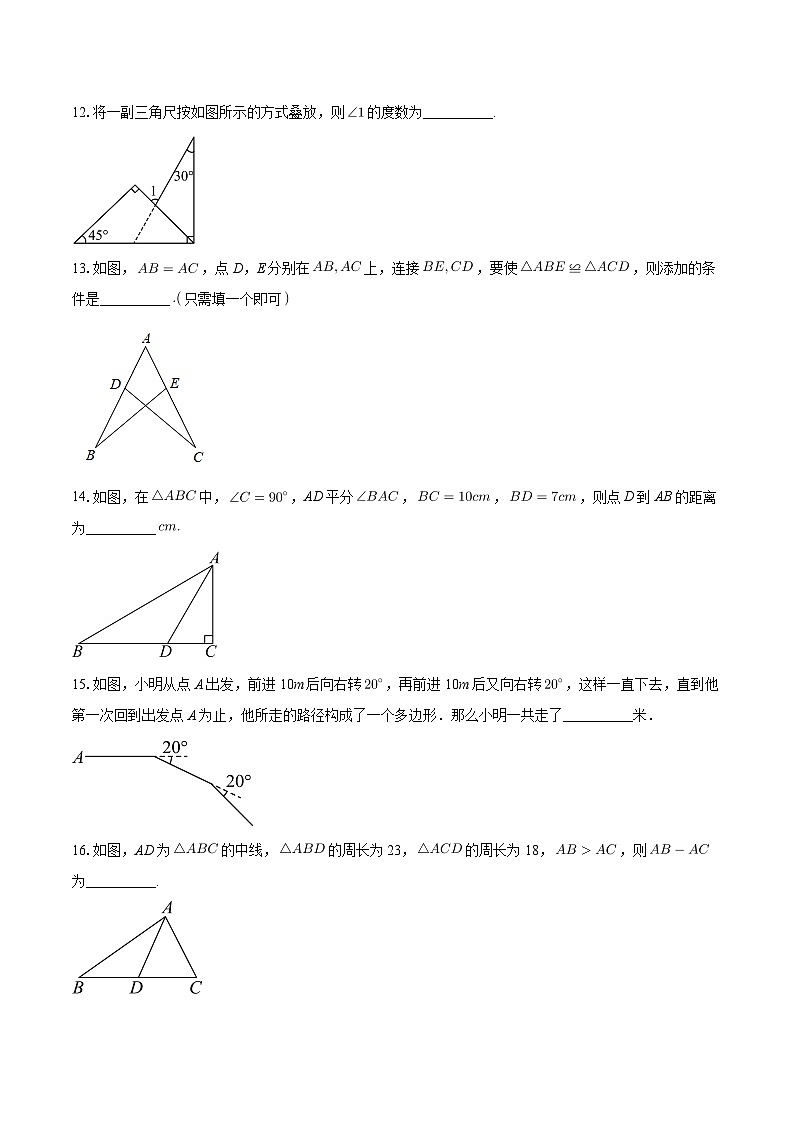
12.将一副三角尺按如图所示的方式叠放，则的度数为__________.
13.如图，，点D，E分别在上，连接，要使≌，则添加的条件是__________只需填一个即可
14.如图，在中，，AD平分，，，则点D到AB的距离为__________
15.如图，小明从点A出发，前进10m后向右转，再前进10m后又向右转，这样一直下去，直到他第一次回到出发点A为止，他所走的路径构成了一个多边形．那么小明一共走了__________米．
16.如图，AD为的中线，的周长为23，的周长为18，，则为__________.
17.如图，已知的内角，分别作内角与外角的平分线，两条平分线交于点，得；和的平分线交于点，得；…，以此类推得到，则的度数是__________.
三、解答题：本题共8小题，共64分。解答应写出文字说明，证明过程或演算步骤。
18.本小题8分
求出下列图中x的值．
19.本小题8分
一个多边形的内角和是外角和的5 倍，求这个多边形的边数．
20.本小题8分
如图，在中，AD是角平分线，AE是高，已知，，求的度数．
21.本小题8分
如图，D是中BC边上一点，
尺规作图：作的平分线，交AB于点保留作图痕迹，不写作法；
在的条件下，求证：
22.本小题8分
如图，，，

求证：
求证：
23.本小题8分
如图，于E，于F，若、

求证：；
求证：
24.本小题8分
如图，在与中，，，，BD与CE相交于点

求证：；
求证：
25.本小题8分
如图，，，，，点P在线段AB上以的速度，由A向B运动，同时点Q在线段BD上由B向D运动．

如图1，若点Q的运动速度与点P的运动速度相等，当运动时间，与是否全等？说明理由，并直接判断此时线段PC和线段PQ的位置关系；
如图2，将“，”为改“”，其他条件不变，若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能使与全等．
在图2的基础上延长AC，BD交于点E，使C，D分别是AE，BE中点，如图3，若点Q以中的运动速度从点B出发，点P以原来速度从点A同时出发，都逆时针沿三边运动，求出经过多长时间点P与点Q第一次相遇．
答案和解析
1.【答案】D
【解析】【分析】三角形的三边关系：三角形的任意两边之和大于第三边，任意两边之差小于第三边，根据原理分别计算两条较短边的和与最长边比较，再逐一分析即可.
【详解】解：故A不符合题意；
故B不符合题意；
故C不符合题意；
故D符合题意；
故选D
2.【答案】C
【解析】【分析】窗框与钉上的木条形成三角形，是利用三角形稳定性；张开的梯腿地面形成三角形，是利用三角形稳定性；伸缩门的结构是平行四边形，不是利用三角形稳定性；张开的马扎腿形成三角形，是利用三角形稳定性．
【详解】A、木窗框与对角钉的木条形成的三角形，三边和三角固定，防止安装变形，是利用三角形的稳定性；
B、活动梯子，张开的梯腿与地面形成三角形，三边和三角固定，防止登上变形，是利用三角形的稳定性；
C、伸缩门的结构是平行四边形，四角活动可以变形开关门，是利用四边形的不稳定性，不是利用三角形的稳定性；
D、小马扎的座面与张开的马扎腿形成三角形，三边与三角固定，防止坐上变形，是利用三角形的稳定性．
故选：
3.【答案】B
【解析】【分析】
根据多边形的内角和的公式，解方程即可求出n的值．
【详解】
解：由多边形的内角和公式可得
，
解得：，
故选：
4.【答案】A
【解析】【分析】根据三角形高的定义解答即可．
【详解】A、AD是中BC边上的高，符合题意；
B、DB不是中BC边上的高，不符合题意；
C、DB是中AC边上的高，不符合题意；
D、，是AB边上的高，不符合题意；
故选：
5.【答案】B
【解析】【分析】分两种情况：当4为腰长，8为底边长时，不符合三角形三边关系，该三角形不存在；当8为腰长，4为底边长时，符合三角形三边关系，即而可以求出周长．
【详解】解：分两种情况：
当4为腰长，8为底边长时，
，不符合三角形三边关系，
该三角形不存在；
当8为腰长，4为底边长时，
，符合三角形三边关系，
该三角形周长为：；
故选：
6.【答案】B
【解析】【分析】根据题意应先假定选择哪块，再对应三角形全等判定的条件进行验证．
【详解】解：1、2块玻璃不同时具备包括一完整边在内的三个证明全等的要素，所以不能带它们去，
只有第3块有完整的两角及夹边，符合ASA，满足题目要求的条件，是符合题意的，
故选：
7.【答案】D
【解析】【分析】根据折叠的性质得到，，一，再根据平角的性质和三角形内角和定理得出答案.
【详解】因为折叠使，，所以，因为，所以，即，同理求出，因为的内角和，所以，即
8.【答案】B
【解析】【分析】根据三角形中线的性质，可得，，，，再根据，求解即可．
【详解】解：点E、F分别为中线AD、中线CE的中点
，，，
又
，即，
故选：
9.【答案】B
【解析】【分析】根据角平分线的定义可得，根据三角形内角和定理可得，则，在中，根据三角形内角和定理即可求解．
【详解】解：如图所示，

、OC分别平分、，
在中，
在中，，
故选：
10.【答案】A
【解析】【分析】连接AD，过D分别作于F、G，则由的面积等于三个小三角形的面积之和可得解答．
【详解】解：如图，连接AD，过D分别作于F、G，

，CD分别是和的角平分线，过点D作于点
由角平分线的性质定理可得：，
，
故选
11.【答案】360
【解析】【分析】根据多边形的外角和等于解答．
【详解】解：十边形的外角和是
故答案为：
12.【答案】度
【解析】【分析】根据三角形外角性质求解即可．
【详解】解：如图，
，，
，
，
故答案为：
13.【答案】答案不唯一
【解析】【分析】根据全等三角形的判定方法，为公共角，，可根据ASA的判定方法进行添加条件即可得出答案．
【详解】解：在和中，
，
≌
故答案为：答案不唯一
14.【答案】3
【解析】解：，，
由角平分线的性质，得点D到AB的距离等于CD的长，
点D到AB的距离为
故答案为
15.【答案】180
【解析】【分析】分析得出所走路径为正多边形，根据正多边形的外角和为，判断多边形的边数，再求路程．
【详解】解：小明每次都是右转且走的路程相同，
走过的路线是正多边形，且每一个外角是，
边数为：，
小明一共走的路程为：
故答案为：
16.【答案】5
【解析】【分析】根据三角形的周长和中线的定义求AB与AC的差．
【详解】解：是的中线，
的周长为23，的周长为18，
，
，
即
故答案为：
17.【答案】
【解析】【分析】根据角平分线的定义可得，，再根据三角形的一个外角等于与它不相邻的两个内角的和可得，，整理即可求出的度数，同理求出，可以发现后一个角等于前一个角的，根据此规律即可得解．
【详解】解：是的平分线，是的平分线，
，，
又，，
，
，
，
；
同理可得，
，
，
故答案为：
18.【答案】；
【解析】【分析】根据三角形的外角等于两个不相邻的内角的和，即可求解；
根据五边形的内角和即可列方程求解．
【详解】解：根据三角形外角的性质可得：，
解得：；
根据五边形的内角和是可得：，
解得：
19.【答案】这个多边形的边数是12
【解析】【分析】根据多边形的内角和公式和外角和定理列出方程，然后求解即可．
【详解】解：设多边形的边数为n，
由题意得，，
解得
故这个多边形的边数是
20.【答案】
【解析】【分析】根据三角形内角和定理，求得和的度数，再根据角平分线的定义，即可求解．
【详解】解：是高，
，
又，，
，，
是角平分线，
，
；
21.【答案】如图：
平分，
，而，
，即，

【解析】【分析】利用基本作图作的平分线DE；
利用角平分线定义得到，再根据三角形外角性质得，加上，从而得到，然后根据平行线的判定方法得到结论．
【详解】如图：
平分，
，而，
，即，
22.【答案】证明： ，
，
，
，
，
≌ ，
，
；
≌ ，
， ，
，
，
≌ ，
.

【解析】【分析】先证明，，结合，可得≌，可得，从而可得结论；
由≌，可得，，可得，结合，证明≌，可得
【详解】证明：，
，
，
，
，
≌，
，
；
≌，
，，
，
，
≌，
23.【答案】证明： ， ，
，
在 和 中，
，
≌ ，
.
于 E ， 于 F ，
，
在 和 中，
，
≌ ，
，
，
.

【解析】【分析】由“HL”可证即可得到结论；
由于E，于F，结合，证明≌，即可得出结论．
【详解】证明：，，
，
在和中，
，
≌，
于E，于F，
，
在和中，
，
≌，
，
，
24.【答案】证明： ，
，即 ，
， ，
≌
.
≌ ，
，
如图，记 的交点为 K ，

， ，
，
.

【解析】【分析】先证明，再利用SAS证明≌即可；
先证明，如图，记的交点为K，结合三角形的内角和定理证明，从而可得结论．
【详解】证明：，
，即，
，，
≌
≌，
，
如图，记的交点为K，

，，
，
25.【答案】全等，理由如下：
当 时， ， ，
又 ，
在 与 中，
，
≌ ，
，
，
，
线段 PC 与线段 PQ 垂直．
；垂直

【解析】【分析】利用SAS证得≌，得出，进一步得出，得出结论即可；
由，分两种情况：①，，建立方程组求解后发现此时点Q的运动速度与点P的运动速度相等，与题目不符，故舍去；②，，建立方程组求得答案即可；
因为Q以中的运动速度从点B出发，点P以原来速度从点A同时出发，都逆时针沿三边运动，只能是Q点绕圈追上P点，即点P比点Q多走的路程，据此列出方程，解这个方程即可．
【详解】全等，理由如下：
当时，，，
又，
在与中，
，
≌，
，
，
，
线段PC与线段PQ垂直．
设点Q的运动速度，
①若≌，则，，
，
解得，
由于此时点Q的运动速度与点P的运动速度相等，不合题意，故舍去此种情况；
②若≌，则，，
，
解得，
综上所述，当点Q的运动速度为时，能使与全等．
，D分别是AE，BE中点，，
，
以中的运动速度从点B出发，点P以原来速度从点A同时出发，都逆时针沿三边运动，
只能是Q点绕圈追上P点，即点Q比点P多走的路程，设运动时间为m秒，
列方程：，
解得：，
故经过24s，点P与点Q第一次相遇．