

所属成套资源:中考数学总复习举一反三系列(通用版)(原卷版+解析)
- 中考数学总复习举一反三系列(通用版)专题25投影与视图(10个高频考点)(全国通用)(原卷版+解析) 试卷 0 次下载
- 中考数学总复习举一反三系列(通用版)专题25投影与视图(10个高频考点)(强化训练)(全国通用)(原卷版+解析) 试卷 0 次下载
- 中考数学总复习举一反三系列(通用版)专题26图形的对称、平移、旋转与位似(10个高频考点)(强化训练)(全国通用)(原卷版+解析) 试卷 0 次下载
- 中考数学总复习举一反三系列(通用版)专题27统计(10个高频考点)(全国通用)(原卷版+解析) 试卷 0 次下载
- 中考数学总复习举一反三系列(通用版)专题27统计(10个高频考点)(强化训练)(全国通用)(原卷版+解析) 试卷 0 次下载
中考数学总复习举一反三系列(通用版)专题26图形的对称、平移、旋转与位似(10个高频考点)(全国通用)(原卷版+解析)
展开
这是一份中考数学总复习举一反三系列(通用版)专题26图形的对称、平移、旋转与位似(10个高频考点)(全国通用)(原卷版+解析),共48页。
TOC \ "1-1" \h \u
\l "_Tc5649" 【考点1 利用平移的性质求解】 PAGEREF _Tc5649 \h 1
\l "_Tc211" 【考点2 坐标轴中的平移】 PAGEREF _Tc211 \h 3
\l "_Tc12687" 【考点3 镜面对称】 PAGEREF _Tc12687 \h 4
\l "_Tc32320" 【考点4 轴对称中坐标与图形变化】 PAGEREF _Tc32320 \h 5
\l "_Tc9647" 【考点5 设计轴对轴图案】 PAGEREF _Tc9647 \h 5
\l "_Tc18509" 【考点6 利用轴对称求最值】 PAGEREF _Tc18509 \h 6
\l "_Tc4449" 【考点7 利用旋转的性质求解】 PAGEREF _Tc4449 \h 8
\l "_Tc28745" 【考点8 旋转中的坐标与图形变换】 PAGEREF _Tc28745 \h 9
\l "_Tc32340" 【考点9 位似变换】 PAGEREF _Tc32340 \h 10
\l "_Tc2140" 【考点10 图形的变换与作图】 PAGEREF _Tc2140 \h 12
【知识点 平移】
(1)定义:把一个图形沿着某一直线方向移动,这种图形的平行移动,简称为平移。
(2)平移的性质:平移后的图形与原图形全等;对应角相等;对应点所连的线段平行(或在同一条直线上)且相等。
(3)坐标的平移: 点(x,y)向右平移a个单位长度后的坐标变为(x+a,y);
点(x,y)向左平移a个单位长度后的坐标变为(x-a,y);
点(x,y)向上平移a个单位长度后的坐标变为(x,y+a);
点(x,y)向下平移a个单位长度后的坐标变为(x,y-a)。
【考点1 利用平移的性质求解】
【例1】(2022春·广东江门·九年级模拟预测)如图,长方形ABCD的长AB为8,宽AD为6,将这个长方形向上平移3个单位,再向左平移2个单位,得到长方形EFGH,则阴影部分的面积为( )
A.30B.32C.36D.40
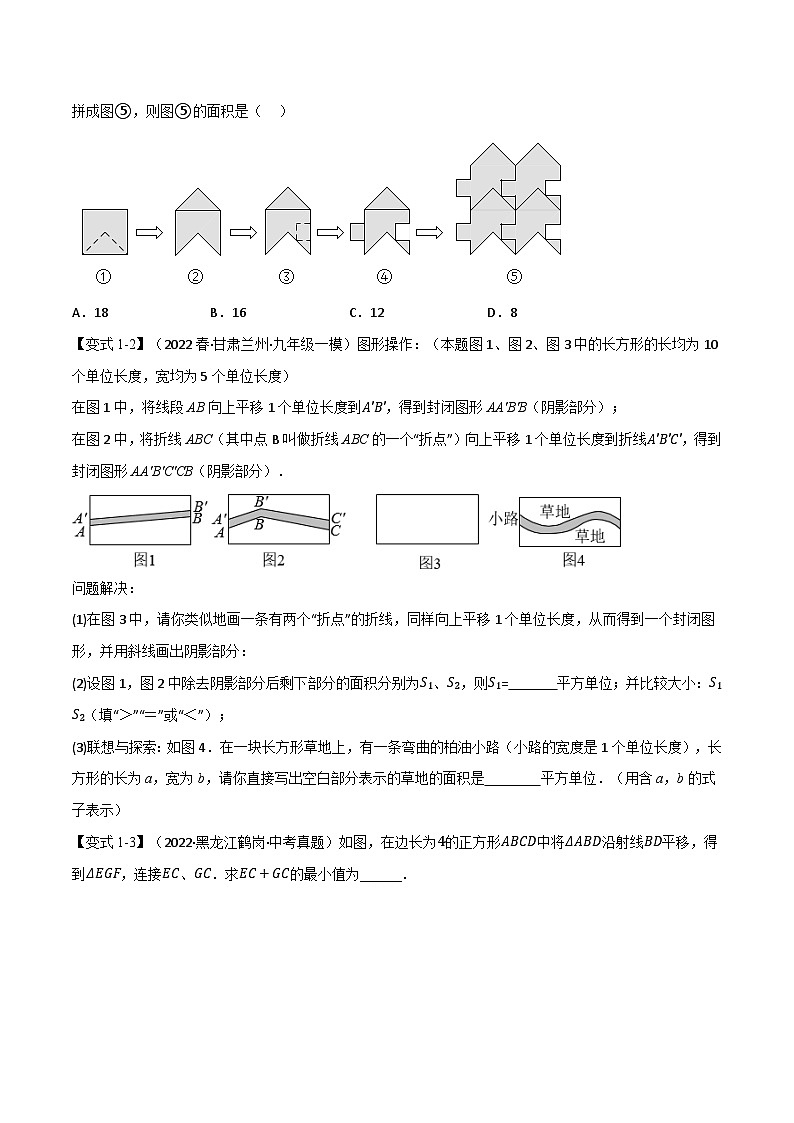
【变式1-1】(2022春·广东韶关·九年级一模)如图,把边长为2的正方形的局部进行图①~图④的变换,拼成图⑤,则图⑤的面积是( )
A.18B.16C.12D.8
【变式1-2】(2022春·甘肃兰州·九年级一模)图形操作:(本题图1、图2、图3中的长方形的长均为10个单位长度,宽均为5个单位长度)
在图1中,将线段AB向上平移1个单位长度到A′B′,得到封闭图形AA'B'B(阴影部分);
在图2中,将折线ABC(其中点B叫做折线ABC的一个“折点”)向上平移1个单位长度到折线A′B′C′,得到封闭图形AA'B'C'CB(阴影部分).
问题解决:
(1)在图3中,请你类似地画一条有两个“折点”的折线,同样向上平移1个单位长度,从而得到一个封闭图形,并用斜线画出阴影部分:
(2)设图1,图2中除去阴影部分后剩下部分的面积分别为S1、S2,则S1= 平方单位;并比较大小:S1 S2(填“>”“=”或“<”);
(3)联想与探索:如图4.在一块长方形草地上,有一条弯曲的柏油小路(小路的宽度是1个单位长度),长方形的长为a,宽为b,请你直接写出空白部分表示的草地的面积是 平方单位.(用含a,b的式子表示)
【变式1-3】(2022·黑龙江鹤岗·中考真题)如图,在边长为4的正方形ABCD中将ΔABD沿射线BD平移,得到ΔEGF,连接EC、GC.求EC+GC的最小值为______.
【考点2 坐标轴中的平移】
【例2】(2022春·黑龙江齐齐哈尔·九年级模拟预测)如图,在平面直角坐标系中,A−2,0,将点A向下平移1个单位,再向右平移2个单位得到点B,若点C在y轴上,且S△ABC=3,则点C的坐标为______.
【变式2-1】(2022春·广东珠海·九年级模拟预测)如图,在平面直角坐标系中,AP∥DF∥x轴,AB∥CD∥GF∥PH∥y轴,点C、B、H、G在x轴上,A(−1,2),C(−3,0),D(−3,−2),F(3,−2),P(1,2),把一条长为2022个单位长度且没有弹性的细线(粗细忽略不计)的一端固定在点A处,并按A−B−C−D−E−F−G−H−P−A⋯的规律紧绕在图形“凸”的边上,则细线另一端所在位置的点的坐标是_______.
【变式2-2】(2022春·山东滨州·九年级校联考)如图,在平面直角坐标系中A−1,1,B−1,−2,C3,−2,D3,1,一只瓢虫从点A出发以2个单位长度/秒的速度沿A→B→C→D→A循环爬行,问第2021秒瓢虫在( )处.
A.3,1B.−1,−2C.1,−2D.3,−2
【变式2-3】(2022秋·河北保定·九年级模拟预测)点Em,n在平面直角坐标系中的位置如图所示,则坐标m+1,n−1对应的点可能是( )
A.A点B.B点C.C点D.D点
【考点3 镜面对称】
【例3】(2022·河南·一模)小狗皮皮看到镜子里的自己,觉得很奇怪,此时它所看到的全身像是( )
A.(A)B.(B)C.(C)D.(D)
【变式3-1】(2012·湖南郴州·一模)小强站在镜前,从镜子中看到镜子对面墙上挂着的电子表,其读数如图所示,则电子表的实际时刻是____________.
【变式3-2】(2022·广东湛江·一模)一个汽车牌在水中的倒影为,则该车牌照号码___________.
【变式3-3】(2022·浙江温州·一模)某电梯中一面镜子正对楼层显示屏,显示屏中显示的是电梯所在楼层号和电梯运行方向.当电梯中镜子如图显示时,电梯所在楼层号为______.
【考点4 轴对称中坐标与图形变化】
【例4】(2022·贵州省遵义市第一初级中学九年级一模)已知点P1(2a−b,2)和P2(−7,4a+2b)关于x轴对称,则ab=__.
【变式4-1】(2022·内蒙古·霍林郭勒市第五中学九年级一模)将点A先向下平移3个单位,再向右平移2个单位后得B(﹣2,5),则A点关于y轴的对称点坐标为__________.
【变式4-2】(2022秋·河南安阳模拟预测)已知点P(2a+b,-3a)与点P′(8,b+2).
(1)若点p与点p′关于x轴对称,求a、b的值.
(2)若点p与点p′关于y轴对称,求a、b的值.
【变式4-3】(2022·吉林白山·九年级模拟预测)在坐标平面上有一个轴对称图形,其中A(3,﹣52)和B(3,﹣112)是图形上的一对对称点,若此图形上另有一点C(﹣2,﹣9),则C点对称点的坐标是( )
A.(﹣2,1)B.(﹣2,﹣32)C.(﹣32,﹣9)D.(﹣2,﹣1)
【考点5 设计轴对轴图案】
【例5】(2022·江苏·九年级课时练习)如图所示的“钻石”型网格(由边长都为1个单位长度的等边三角形组成),其中已经涂黑了3个小三角形(阴影部分表示),请你再只涂黑一个小三角形,使它与阴影部分合起来所构成的图形是一个轴对称图形,一共有( )种涂法.
A.1B.2C.3D.4
【变式5-1】(2022·河北·九年级专题练习)如图为5×5的方格,其中有A、B、C三点,现有一点P在其它格点上,且A、B、C、P为轴对称图形,问共有几个这样的点P( )
A.5B.4C.3D.2
【变式5-2】(2022春·广东江门·九年级模拟预测)在3×3的正方形网格中,有三个小方格涂上阴影,请再在余下的6个空白的小方格中,选两个小方格并涂成阴影,使得图中的阴影部分组成一个轴对称图形,共有 ( )种不同的填涂方法.
A.3种B.4种C.5种D.6种
【变式5-3】(2022·江苏·九年级专题练习)现有如图1所示的两种瓷砖,请你从两种瓷砖中各选两块,拼成一个新的正方形,使拼成的图案为轴对称图形,如图2,要求:在图3,图4中各设计一种与示例拼法不同的轴对称图形.
【考点6 利用轴对称求最值】
【例6】(2022·湖南·李达中学九年级)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AB=10,AD是∠BAC的平分线,若P,Q分别是AD何AC上的动点,则PC+PQ的最小值是( )
A.2.4B.4C.4.8D.5
【变式6-1】(2022·河南驻马店·九年级模拟预测)如图,四边形ABCD中,∠BAD=α,∠B=∠D=90°,在BC、CD上分别找一点M、N,当△AMN周长最小时,则∠MAN的度数为( )
A.12αB.2α−180°C.180°−αD.α−90°
【变式6-2】(2022·全国·九年级专题练习)如图,在长方形ABCD中,AD=BC=3,AB=CD=4,AC=5,动点M在线段AC上运动(不与端点重合),点M关于边AD,DC的对称点分别为M1,M2,连接M1M2,点D在M1M2上,则在点M的运动过程中,线段M1M2长度的最小值是_______.
【变式6-3】(2022·福建龙岩·九年级一模)如图,在Rt△ABC中,∠A=90°,AB=8,AC=6,BC=10,M、N、P分别是边AB、AC、BC上的动点,连接PM、PN和MN,则PM+PN+MN的最小值是 _______.
【知识点 旋转的定义】
在平面内,把一个平面图形绕着平面内某一点O转动一个角度,就叫做图形的旋转,点O叫做旋转中心,转动的角叫做旋转角。
我们把旋转中心、旋转角度、旋转方向称为旋转的三要素。
【知识点 旋转的性质】
旋转的特征:
(1)对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角;
(3)旋转前后的图形全等。
理解以下几点:
(1)图形中的每一个点都绕旋转中心旋转了同样大小的角度。
(2)对应点到旋转中心的距离相等,对应线段相等,对应角相等。
(3)图形的大小与形状都没有发生改变,只改变了图形的位置。
【考点7 利用旋转的性质求解】
【例7】(2022春•梅州校级模拟预测)如图,点O是等边△ABC内一点,∠AOB=110°,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,若OD=AD,则∠BOC的度数为 140° .
【变式7-1】(2022•东莞市校级一模)如图,△AOB中,∠AOB=90°,AO=4,BO=8,△AOB绕点O逆时针旋转到△A′OB′处,此时线段A′B′与BO的交点E为BO的中点,则线段B′E的长度为( )
A.35B.1255C.955D.1655
【变式7-2】(2022•城步县模拟)如图,P为等边三角形ABC内一点,∠APB:∠APC:∠CPB=5:6:7,则以PA,PB,PC为三边构成的三角形的三个内角从小到大的度数之比为( )
A.1:2:3B.2:3:4C.3:4:5D.5:6:7
【变式7-3】(2022春•和平区模拟预测)如图,△ABC与△CDE都是等边三角形,连接AD,BE,CD=4,BC=2,若将△CDE绕点C顺时针旋转,当点A、C、E在同一条直线上时,线段BE的长为( )
A.23B.27C.3或7D.23或27
【考点8 旋转中的坐标与图形变换】
【例8】(2022秋•黄石模拟预测)如图,线段AB与线段CD关于点P对称,若点A(a,b)、B(5,1)、D(﹣3,﹣1),则点C的坐标为( )
A.(﹣a,﹣b)B.(﹣a+2,﹣b)
C.(﹣a﹣1,﹣b+1)D.(﹣a+1,﹣b﹣1)
【变式3-1】(2022秋•本溪模拟预测)如图,在△AOB中,OA=4,OB=6,AB=27,将△AOB绕原点O逆时针旋转90°,则旋转后点A的对应点A′的坐标是( )
A.(﹣4,2)B.(﹣23,4)C.(﹣23,2)D.(﹣2,23)
【变式3-2】(2022秋•西湖区模拟预测)如图,在平面直角坐标系中,△MNP绕原点逆时针旋转90°得到△M1N1P1,若M(1,﹣2),则点M1的坐标为( )
A.(﹣2,﹣1)B.(1,2)C.(2,1)D.(﹣1,﹣2)
【变式3-3】(2022•新抚区模拟)如图,Rt△AOB的斜边AO在y轴上,OB=3,∠AOB=30°,直角顶点B在第二象限,将Rt△AOB绕原点O顺时针旋转120°后得到△A′OB',则A点的对应点A′的坐标是( )
A.(3,﹣1)B.(1,−3)C.(2,0)D.(3,0)
【考点9 位似变换】
【例9】(2022春•如皋市模拟预测)若△ABC绕点A逆时针旋转α后,与△ADE构成位似图形,则我们称△ABC与△ADE互为“旋转位似图形”.
(1)知识理解:
如图1,△ABC与△ADE互为“旋转位似图形”.
①若α=25°,∠D=100°,∠C=28°,则∠BAE= ;
②若AD=6,DE=7,AB=4,则BC=
(2)知识运用:
如图2,在四边形ABCD中,∠ADC=90°,AE⊥BD于点E,∠DAC=∠DBC,求证:△ACD与△ABE互为“旋转位似图形”.
(3)拓展提高:
如图3,△ABG为等边三角形,点C为AG的中点,点F是AB边上的一点,点D为CF延长线上的一点,点E在线段CF上,且△ABD与△ACE互为“旋转位似图形”.若AB=6,AD=4,求DECE的值.
【变式9-1】(2022·山东潍坊·中考真题)《墨子·天文志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形ABCD的面积为4,以它的对角线的交点为位似中心,作它的位似图形A′B′C′D′,若A′B′:AB=2:1,则四边形A′B′C′D′的外接圆的周长为___________.
【变式9-2】(2022·贵州黔西·中考真题)如图,△A′B′C′与△ABC是位似图形,点O为位似中心,若OA′=A′A,则△A′B′C′与△ABC的面积比为__.
【变式9-3】(2022·安徽·中考真题)如图,在由边长为1个单位长度的小正方形组成的10×10网格中,已知点O,A,B均为网格线的交点.
(1)在给定的网格中,以点O为位似中心,将线段AB放大为原来的2倍,得到线段A1B1(点A,B的对应点分别为A1、B1).画出线段A1B1;
(2)将线段A1B1绕点B1逆时针旋转90°得到线段A2B1.画出线段A2B1;
(3)以A、A1、B1、A2为顶点的四边形AA1B1A2的面积是_______个平方单位.
【考点10 图形的变换与作图】
【例10】(2022春•化州市校级一模)如图,在平面直角坐标系中,△ABC的三个顶点分别是A(1,3),B(4,4),C(2,1).
(1)把△ABC向左平移4个单位后得到对应的△A1B1C1,请画出平移后的△A1B1C1;
(2)把△ABC绕原点O旋转180°后得到对应的△A2B2C2,请画出旋转后的△A2B2C2.
【变式10-1】(2022春·北京怀柔·九年级模拟预测)如图,在平面直角坐标系中,三角形ABC的三个顶点分别是A(0,4),B(-4,1),C(-1,2).
请你解答下列问题:
(1)在平面直角坐标系中画出三角形ABC;
(2)将三角形ABC先向下平移5个单位,再向右平移3个单位.画出平移后的三角形A1B1C1.
(3)把(2)三角形A1B1C1各个顶点的横坐标保持不变,纵坐标增加2,得到三角形A2B2C2.直接写出三角形A2B2C2的面积.
【变式10-2】(2022·广西桂林·中考真题)如图,在平面直角坐标系中,形如英文字母“V”的图形三个端点的坐标分别是A(2,3),B(1,0),C(0,3).
(1)画出“V”字图形向左平移2个单位后的图形;
(2)画出原“V”字图形关于x轴对称的图形;
(3)所得图形与原图形结合起来,你能从中看出什么英文字母?(任意答一个即可)
【变式10-3】(2022春•蒲城县模拟预测)在如图所示的平面直角坐标系中,每个小方格都是边长为1个单位长度的正方形,△ABC的顶点坐标分别为A(1,1),B(3,0),C(2,3).
(1)将△ABC向左平移4个单位长度得到△A1B1C1,点A、B、C的对应点分别为A1、B1、C1,请画出△A1B1C1,并写出点C1的坐标;
(2)以原点O为旋转中心,将△ABC顺时针旋转90°得到△A2B2C2,点A、B、C的对应点分别为A2、B2、C2,请画出△A2B2C2.
专题26 图形的对称、平移、旋转与位似(10个高频考点)(举一反三)
TOC \ "1-1" \h \u
\l "_Tc5649" 【考点1 利用平移的性质求解】 PAGEREF _Tc5649 \h 1
\l "_Tc211" 【考点2 坐标轴中的平移】 PAGEREF _Tc211 \h 6
\l "_Tc12687" 【考点3 镜面对称】 PAGEREF _Tc12687 \h 9
\l "_Tc32320" 【考点4 轴对称中坐标与图形变化】 PAGEREF _Tc32320 \h 10
\l "_Tc9647" 【考点5 设计轴对轴图案】 PAGEREF _Tc9647 \h 12
\l "_Tc18509" 【考点6 利用轴对称求最值】 PAGEREF _Tc18509 \h 15
\l "_Tc4449" 【考点7 利用旋转的性质求解】 PAGEREF _Tc4449 \h 20
\l "_Tc28745" 【考点8 旋转中的坐标与图形变换】 PAGEREF _Tc28745 \h 25
\l "_Tc32340" 【考点9 位似变换】 PAGEREF _Tc32340 \h 28
\l "_Tc2140" 【考点10 图形的变换与作图】 PAGEREF _Tc2140 \h 33
【知识点 平移】
(1)定义:把一个图形沿着某一直线方向移动,这种图形的平行移动,简称为平移。
(2)平移的性质:平移后的图形与原图形全等;对应角相等;对应点所连的线段平行(或在同一条直线上)且相等。
(3)坐标的平移: 点(x,y)向右平移a个单位长度后的坐标变为(x+a,y);
点(x,y)向左平移a个单位长度后的坐标变为(x-a,y);
点(x,y)向上平移a个单位长度后的坐标变为(x,y+a);
点(x,y)向下平移a个单位长度后的坐标变为(x,y-a)。
【考点1 利用平移的性质求解】
【例1】(2022春·广东江门·九年级模拟预测)如图,长方形ABCD的长AB为8,宽AD为6,将这个长方形向上平移3个单位,再向左平移2个单位,得到长方形EFGH,则阴影部分的面积为( )
A.30B.32C.36D.40
【答案】A
【分析】利用平移的性质求得HM=BN=2,DM=FN=3,根据阴影部分的面积=长方形ABCD的面积-长方形AMGN的面积,求解即可.
【详解】解:如图,
∵将这个长方形向上平移3个单位,再向左平移2个单位,
∴HM=BN=2,DM=FN=3
∵长方形ABCD的长AB为8,宽AD为6,
∴AM=AD−DM=6−3=3,AN=AB−BN=8−2=6,
∴长方形AMGN=AM×AN= 3×6=18,
∴阴影部分的面积为8×6−18=30,
故选:A.
【点睛】本题考查了平移的性质,掌握平移的性质是解题的关键.平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.
【变式1-1】(2022春·广东韶关·九年级一模)如图,把边长为2的正方形的局部进行图①~图④的变换,拼成图⑤,则图⑤的面积是( )
A.18B.16C.12D.8
【答案】B
【分析】根据平移的基本性质,平移不改变图形的形状和大小,即图形平移后面积不变,则⑤的面积为4个正方形的面积和,即可得到结论.
【详解】解:一个正方形面积为2×2=4,而把一个正方形从①﹣④变换,面积并没有改变,所以图⑤由4个图④构成,故图⑤面积为4×4=16,故B正确.
故选:B.
【点睛】本题主要考查了图形拼接与平移的变换,解答本题的关键是要知道平移不改变图形的形状和大小,即面积没有改变.
【变式1-2】(2022春·甘肃兰州·九年级一模)图形操作:(本题图1、图2、图3中的长方形的长均为10个单位长度,宽均为5个单位长度)
在图1中,将线段AB向上平移1个单位长度到A′B′,得到封闭图形AA'B'B(阴影部分);
在图2中,将折线ABC(其中点B叫做折线ABC的一个“折点”)向上平移1个单位长度到折线A′B′C′,得到封闭图形AA'B'C'CB(阴影部分).
问题解决:
(1)在图3中,请你类似地画一条有两个“折点”的折线,同样向上平移1个单位长度,从而得到一个封闭图形,并用斜线画出阴影部分:
(2)设图1,图2中除去阴影部分后剩下部分的面积分别为S1、S2,则S1= 平方单位;并比较大小:S1 S2(填“>”“=”或“<”);
(3)联想与探索:如图4.在一块长方形草地上,有一条弯曲的柏油小路(小路的宽度是1个单位长度),长方形的长为a,宽为b,请你直接写出空白部分表示的草地的面积是 平方单位.(用含a,b的式子表示)
【答案】(1)见解析过程;
(2)40,=;
(3)(ab-a)
【分析】(1)画一条有两个“折点”的折线,同样向上平移1个单位长度,从而得到一个封闭图形AA'B'C'D'DCB;
(2)依据平移变换可知,图1,图2中除去阴影部分后剩下部分可以拼成一个长为10个单位,宽为4个单位的长方形,进而得出其面积;
(3)依据平移变换可知,图3中除去阴影部分后剩下部分可以拼成一个长为a个单位,宽为(b-1)个单位的长方形,进而得出其面积.
【详解】(1)如图3所示,封闭图形AA'B'C'D'DCB即为所求;
(2)图1,图2中除去阴影部分后剩下部分的面积分别为S1、S2,
则S1=10×(5-1)=10×4=40平方单位;
S2=10×(5-1)=10×4=40平方单位;
∴S1=S2,
故答案为:40,=;
(3)如图4,长方形的长为a,宽为b,小路的宽度是1个单位长度,
∴空白部分表示的草地的面积是a(b-1)=(ab-a)平方单位.
故答案为:(ab-a).
【点睛】本题属于几何变换综合题,主要考查了平移变换以及矩形面积的计算公式的运用,解决问题的关键是利用平移的性质,把不规则的图形拆分或拼凑为基本图形来计算面积.
【变式1-3】(2022·黑龙江鹤岗·中考真题)如图,在边长为4的正方形ABCD中将ΔABD沿射线BD平移,得到ΔEGF,连接EC、GC.求EC+GC的最小值为______.
【答案】45
【分析】将△ABC沿射线CA平移到△AB′C′的位置,连接C′E、AE、DE,证出四边形ABGE和四边形EGCD均为平行四边形,根据平行四边形的性质和平移图形的性质,可得C′E=CE,CG=DE,可得EC+GC=C′E+ED,当点C′、E、D在同一直线时,C′E+ED最小,由勾股定理求出C′D的值即为EC+GC的最小值.
【详解】如图,将△ABC沿射线CA平移到△AB′C′的位置,连接C′E、AE、DE,
∵AB∥GE∥DC且AB=GE=DC,
∴四边形ABGE和四边形EGCD均为平行四边形,
∴AE∥BG,CG=DE,
∴AE⊥CC′,
由作图易得,点C与点C′关于AE对称,C′E=CE,
又∵CG=DE,
∴EC+GC=C′E+ED,
当点C′、E、D在同一直线时,C′E+ED最小,
此时,在Rt△C′D′E中,
C′B′=4,B′D=4+4=8, C′D=42+82=45,
即EC+GC的最小值为45,
故答案为:45.
【点睛】本题考查正方形的性质、图形的对称性、线段最短和平行四边形的性质与判定,解题的关键是将两条线段的和转化为同一条线段求解.
【考点2 坐标轴中的平移】
【例2】(2022春·黑龙江齐齐哈尔·九年级模拟预测)如图,在平面直角坐标系中,A−2,0,将点A向下平移1个单位,再向右平移2个单位得到点B,若点C在y轴上,且S△ABC=3,则点C的坐标为______.
【答案】(0,2)或(0,−4)
【分析】根据题意确定点B的坐标,然后设C(0,m),结合图形,利用面积得出方程求解即可.
【详解】解:将点A向下平移1个单位,再向右平移2个单位得到点B,
∴B(0,−1),
设C(0,m),
如图所示,
根据题意得:12×m+1×2=3,
解得:m=2或−4,
∴C(0,2)或(0,−4),
故答案为:(0,2)或(0,−4).
【点睛】题目主要考查坐标与图形,坐标的平移,一元一次方程的应用等,理解题意,综合运用这些知识点是解题关键.
【变式2-1】(2022春·广东珠海·九年级模拟预测)如图,在平面直角坐标系中,AP∥DF∥x轴,AB∥CD∥GF∥PH∥y轴,点C、B、H、G在x轴上,A(−1,2),C(−3,0),D(−3,−2),F(3,−2),P(1,2),把一条长为2022个单位长度且没有弹性的细线(粗细忽略不计)的一端固定在点A处,并按A−B−C−D−E−F−G−H−P−A⋯的规律紧绕在图形“凸”的边上,则细线另一端所在位置的点的坐标是_______.
【答案】(−1,0)
【分析】根据点的坐标、坐标的平移规律可知旋转一周的长度为20,然后可判断细线另一端所在位置的点在B处,再直接求解即可.
【详解】解:∵AP∥DF∥x轴,AB∥CD∥GF∥PH∥y轴,
点C、B、H、G在x轴上,A(−1,2),C(−3,0),D(−3,−2),F(3,−2),P(1,2),
∴B点坐标为(-1,0),点H坐标为(1,0),G(3,0),
∴AP=BH=2,AB=PH=2,CD=GF=2,BC=HG=2,DF=CG=6,
∴按A-B-C-D-E-F-G-H-P-A缠绕一周的总长度为2+2+2+6+2+2+2+2=20,
∵2022÷20=101···2,
∴细线另一端所在位置的点在B点处,
∴细线另一端所在位置的点的坐标为(-1,0).
故答案为:(−1,0).
【点睛】本题主要考查点的坐标、坐标的平移,解决本题的关键是确定缠绕一周的总长度为20.
【变式2-2】(2022春·山东滨州·九年级校联考)如图,在平面直角坐标系中A−1,1,B−1,−2,C3,−2,D3,1,一只瓢虫从点A出发以2个单位长度/秒的速度沿A→B→C→D→A循环爬行,问第2021秒瓢虫在( )处.
A.3,1B.−1,−2C.1,−2D.3,−2
【答案】A
【分析】根据点A、B、C、D的坐标可得出AB、AD及四边形ABCD的周长,由2021÷7=288……5,且5×2=10s,可得出当t=2021秒时,瓢虫在AD上,且距离D点3个单位,即可得出结论.
【详解】解:∵A(−1,1)B(−1,−2),C(3,−2),D(3,1),
∴AB=CD=3,AD=BC=4,
∴四边形ABCD的周长为2AB+AD=14,
∵瓢虫从点A出发以2个单位长度/秒的速度沿A→B→C→D→A循环爬行,
∴瓢虫爬行一个循环所用的时间为142=7s,
∵2021÷7=288……5,且5×2=10s,
∴此时瓢虫在AD上,且距离D点3个单位,
∴此时点瓢虫的坐标为3,1.
故选:A.
【点睛】本题考查了规律型中点的坐标,根据瓢虫的运动规律找出当t=2021秒时,瓢虫所在的位置是解题的关键.
【变式2-3】(2022秋·河北保定·九年级模拟预测)点Em,n在平面直角坐标系中的位置如图所示,则坐标m+1,n−1对应的点可能是( )
A.A点B.B点C.C点D.D点
【答案】C
【分析】由Em,n移动到m+1,n−1,点向右移动1个单位,同时向下移动1个单位,依此观察图形即可求解.
【详解】解:∵由Em,n移动到m+1,n−1,
∴点向右移动1个单位,同时向下移动1个单位,
观察图形可得坐标m+1,n−1对应的点可能是C
故选:C.
【点睛】本题考查了点的坐标,解题的关键是得到点的坐标移动的规律.
【考点3 镜面对称】
【例3】(2022·河南·一模)小狗皮皮看到镜子里的自己,觉得很奇怪,此时它所看到的全身像是( )
A.(A)B.(B)C.(C)D.(D)
【答案】A
【详解】根据题意可知,小狗和镜面里的像是关于镜面对称的,
∴小狗与它的像的对应点的连线应该与镜面垂直,且对应点到镜面的距离相等,
∴上述四个图像中,只有A符合要求,其余三个都不符合要求.
故选A.
【变式3-1】(2012·湖南郴州·一模)小强站在镜前,从镜子中看到镜子对面墙上挂着的电子表,其读数如图所示,则电子表的实际时刻是____________.
【答案】10:51
【分析】根据镜面对称原理,左右颠倒,上下不变即可解题.
【详解】根据镜面对称原理,物体的像与物体本身上下不变,左右颠倒可知,12:01对称之后为10:51.
【点睛】本题考查了镜面对称,属于简单题,熟悉镜面对称的原理是解题关键.
【变式3-2】(2022·广东湛江·一模)一个汽车牌在水中的倒影为,则该车牌照号码___________.
【答案】M17936
【详解】试题分析:本题是轴对称中的镜面对称问题,水面相当于一个平面镜,因为镜面对称的性质是在平面镜中的像与现实中的事物恰好顺序颠倒,且关于镜面对称.故答案为.
考点:轴对称的性质.
【变式3-3】(2022·浙江温州·一模)某电梯中一面镜子正对楼层显示屏,显示屏中显示的是电梯所在楼层号和电梯运行方向.当电梯中镜子如图显示时,电梯所在楼层号为______.
【答案】15
【分析】根据镜面成像的原理:左右相反,即可得到答案.
【详解】解:由镜面成像的原理可知电梯所在的楼层为15,
故答案为:15.
【点睛】本题主要考查了镜面成像,熟知镜面成像的原理是解题的关键.
【考点4 轴对称中坐标与图形变化】
【例4】(2022·贵州省遵义市第一初级中学九年级一模)已知点P1(2a−b,2)和P2(−7,4a+2b)关于x轴对称,则ab=__.
【答案】−8
【分析】根据题意,列关于a、b的二元一次方程组,求解并计算即可;
【详解】∵点P1(2a−b,2)和P2(−7,4a+2b)关于x轴对称,
∴2a−b=−72+(4a+2b)=0
解得a=−2b=3,
∴ab=(−2)3=−8.
故答案为:−8
【点睛】本题考查了关于x轴对称的点的坐标,解二元一次方程组,掌握相关知识并熟练使用,同时注意解题中需注意的事项是本题的解题关键.
【变式4-1】(2022·内蒙古·霍林郭勒市第五中学九年级一模)将点A先向下平移3个单位,再向右平移2个单位后得B(﹣2,5),则A点关于y轴的对称点坐标为__________.
【答案】(4,8)
【分析】设A(x,y),根据向下平移纵坐标减,向右平移横坐标加列方程求解,再根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”解答.
【详解】解:设A(x,y),
∵点A向下平移3个单位,再向右平移2个单位后得B(−2,5),
∴x+2=−2,y−3=5,
解得x=−4,y=8,
∴点A的坐标为(−4,8),
∴A点关于y轴的对称点坐标为(4,8).
故答案为:(4,8).
【点睛】本题考查了坐标的平移规律,以及关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:关于x轴对称的点,横坐标相同,纵坐标互为相反数;关于y轴对称的点,纵坐标相同,横坐标互为相反数.
【变式4-2】(2022秋·河南安阳模拟预测)已知点P(2a+b,-3a)与点P′(8,b+2).
(1)若点p与点p′关于x轴对称,求a、b的值.
(2)若点p与点p′关于y轴对称,求a、b的值.
【答案】(1)a=2,b=4
(2)a=6,b=-20
【分析】(1)根据关于x轴对称的点,横坐标相等、纵坐标互为相反数方程组求解即可;
(2)根据关于y轴对称的点,纵坐标相等、横坐标互为相反数方程组求解即可.
(1)
解:∵点P与点P′关于x轴对称,
∴2a+b=8,3a= b+2,解得a=2, b=4.
(2)
解:∵点P与点P′关于y轴对称,
∴2a+b=-8,-3a= b+2
解得a=6, b=-20.
【点睛】本题主要考查了关于坐标轴对称的点坐标特征,关于x轴对称的点,横坐标相等,纵坐标互为相反数;关于y轴对称的点,纵坐标相等、横坐标互为相反数.
【变式4-3】(2022·吉林白山·九年级模拟预测)在坐标平面上有一个轴对称图形,其中A(3,﹣52)和B(3,﹣112)是图形上的一对对称点,若此图形上另有一点C(﹣2,﹣9),则C点对称点的坐标是( )
A.(﹣2,1)B.(﹣2,﹣32)C.(﹣32,﹣9)D.(﹣2,﹣1)
【答案】A
【分析】先利用点A和点B的坐标特征可判断图形的对称轴为直线y=-4,然后写出点C关于直线y=-4的对称点即可.
【详解】解:∵A(3,﹣52)和B(3,﹣112)是图形上的一对对称点,
∴点A与点B关于直线y=﹣4对称,
∴点C(﹣2,﹣9)关于直线y=﹣4的对称点的坐标为(﹣2,1).
故选:A.
【点睛】本题考查了坐标与图形的变化,需要注意关于直线对称:关于直线x=m对称,则两点的纵坐标相同,横坐标和为2m;关于直线y=n对称,则两点的横坐标相同,纵坐标和为2n.
【考点5 设计轴对轴图案】
【例5】(2022·江苏·九年级课时练习)如图所示的“钻石”型网格(由边长都为1个单位长度的等边三角形组成),其中已经涂黑了3个小三角形(阴影部分表示),请你再只涂黑一个小三角形,使它与阴影部分合起来所构成的图形是一个轴对称图形,一共有( )种涂法.
A.1B.2C.3D.4
【答案】C
【分析】将一个图形沿着某条直线翻折,直线两侧的部分能够完全重合的图形是轴对称图形,根据轴对称图形的概念进行设计即可.
【详解】解:如图所示:
故选:C
【点睛】本题主要考查轴对称图形的概念,解决本题的关键是要熟练掌握轴对称图形的概念.
【变式5-1】(2022·河北·九年级专题练习)如图为5×5的方格,其中有A、B、C三点,现有一点P在其它格点上,且A、B、C、P为轴对称图形,问共有几个这样的点P( )
A.5B.4C.3D.2
【答案】B
【分析】利用轴对称图形的性质得出符合题意的点即可.
【详解】解:如图所示:A、B、C、P为轴对称图形,共有4个这样的点P.
答案:B.
【点睛】此题主要考查了利用轴对称设计图案,正确把握轴对称图形的定义是解题关键.
【变式5-2】(2022春·广东江门·九年级模拟预测)在3×3的正方形网格中,有三个小方格涂上阴影,请再在余下的6个空白的小方格中,选两个小方格并涂成阴影,使得图中的阴影部分组成一个轴对称图形,共有 ( )种不同的填涂方法.
A.3种B.4种C.5种D.6种
【答案】D
【分析】如图,将图中的空白正方形标号,然后根据轴对称图形的定义对其不同的组合进行判断即可.
【详解】解:如图所示:
当将①②、①⑤、②③、②⑥、④⑤、④⑥分别组合,都可以得到轴对称图形,共有6种方法.
故选:D.
【点睛】本题考查了轴对称图形的设计,熟知概念、明确方法是解题的关键.
【变式5-3】(2022·江苏·九年级专题练习)现有如图1所示的两种瓷砖,请你从两种瓷砖中各选两块,拼成一个新的正方形,使拼成的图案为轴对称图形,如图2,要求:在图3,图4中各设计一种与示例拼法不同的轴对称图形.
【答案】见解析
【分析】利用轴对称的性质,以及轴对称的作图方法来作图,通过变换对称轴来得到不同的图案即可.
【详解】解:依照轴对称图形的定义,设计出图形,如图所示.
【点睛】此题主要考查了利用轴对称设计图案,利用轴对称定义得出是解题关键.
【考点6 利用轴对称求最值】
【例6】(2022·湖南·李达中学九年级)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AB=10,AD是∠BAC的平分线,若P,Q分别是AD何AC上的动点,则PC+PQ的最小值是( )
A.2.4B.4C.4.8D.5
【答案】C
【分析】由题意可以把Q反射到AB的O点,如此PC+PQ的最小值问题即变为C与线段AB上某一点O的最短距离问题,最后根据“垂线段最短”的原理得解.
【详解】解:如图,作Q关于AP的对称点O,则PQ=PO,所以O、P、C三点共线时,CO=PC+PO=PC+PQ,此时PC+PQ有可能取得最小值,
∵当CO垂直于AB即CO移到CM位置时,CO的长度最小,
∴PC+PQ的最小值即为CM的长度,
∵S△ABC=12AB×CM=12AC×CB,
∴CM=6×810=4.8,即PC+PQ的最小值为 4.8,
故选C.
【点睛】本题考查了轴对称最短路径问题,垂线段最短,通过轴反射把线段和最小的问题转化为线段外一点到线段某点连线段最短问题是解题关键.
【变式6-1】(2022·河南驻马店·九年级模拟预测)如图,四边形ABCD中,∠BAD=α,∠B=∠D=90°,在BC、CD上分别找一点M、N,当△AMN周长最小时,则∠MAN的度数为( )
A.12αB.2α−180°C.180°−αD.α−90°
【答案】B
【分析】根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,即可得出∠AA′M+∠A″=∠HAA′,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″)即可得出答案.
【详解】解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,
∵∠DAB=α ,
∴∠HAA′=180°−α,
∴∠AA′M+∠A″=∠HAA′=180°−α,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2180°−α=360°−2α,
∴∠MAN=180°−∠AMN+∠ANM=180°−360°−2α=2α−180°.
故选:B.
【点睛】本题主要考查轴对称-最段路线问题,熟练掌握平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出M,N的位置是解题关键.
【变式6-2】(2022·全国·九年级专题练习)如图,在长方形ABCD中,AD=BC=3,AB=CD=4,AC=5,动点M在线段AC上运动(不与端点重合),点M关于边AD,DC的对称点分别为M1,M2,连接M1M2,点D在M1M2上,则在点M的运动过程中,线段M1M2长度的最小值是_______.
【答案】245
【分析】过D作DM'⊥AC于M',连接DM,根据已知,由面积法先求出DM'=125,由M关于边AD,DC的对称点分别为M1,M2,可得DM1=DM=DM2,M1M2=2DM,故线段M1M2长度最小即是DM长度最小,此时DM⊥AC,M与M'重合,即可得M1M2最小值为2DM'=245.
【详解】解:过D作DM'⊥AC于M',连接DM,如图:
长方形ABCD中,AD=BC=3,AB=CD=4,AC=5,
∴S△ADC=12AD•CD=12AC•DM',
∴DM'=AD·CDAC=3×45=125,
∵M关于边AD,DC的对称点分别为M1,M2,
∴DM1=DM=DM2,
∴M1M2=2DM,
线段M1M2长度最小即是DM长度最小,此时DM⊥AC,即M与M'重合,M1M2最小值为2DM'=245.
故答案为:245.
【点睛】本题考查对称变换,涉及三角形面积、点到直线的距离等知识,解题的关键是将求M1M2长度的最小值转化为求DM长度的最小值.
【变式6-3】(2022·福建龙岩·九年级一模)如图,在Rt△ABC中,∠A=90°,AB=8,AC=6,BC=10,M、N、P分别是边AB、AC、BC上的动点,连接PM、PN和MN,则PM+PN+MN的最小值是 _______.
【答案】485
【分析】如图,作点P关于AB,AC的对称点E,F,连接PE,PF,PA,EM,FN,AE,AF.首先证明E,A,F共线,则PM+MN+PN=EM+MN+NF≥EF,推出EF的值最小时,PM+MN+PN的值最小,求出PA的最小值,可得结论.
【详解】解:如图,作点P关于AB,AC的对称点E,F,连接PE,PF,PA,EM,FN,AE,AF.
由对称的性质可知,AE=AP=AF,∠BAP=∠BAE,∠CAP=∠CAF,
∵∠PAB+∠PAC=∠BAC=90°,
∴∠EAF=180°,
∴E,A,F共线,
∵ME=MP,NF=NP,
∴PM+MN+PN=EM+MN+NF,
∵EM+MN+NF≥EF,
∴EF的值最小时,PM+MN+PN的值最小,
∵EF=2PA,
∴当PA⊥BC时,PA的值最小,此时PA=6×810=245,
∴PM+MN+PN≥485,
∴PM+MN+PN的最小值为485.
故答案为:485.
【点睛】本题考查了轴对称最短问题,解题的关键是学会利用轴对称的性质添加辅助线,把问题转化为两点之间线段最短.
【知识点 旋转的定义】
在平面内,把一个平面图形绕着平面内某一点O转动一个角度,就叫做图形的旋转,点O叫做旋转中心,转动的角叫做旋转角。
我们把旋转中心、旋转角度、旋转方向称为旋转的三要素。
【知识点 旋转的性质】
旋转的特征:
(1)对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角;
(3)旋转前后的图形全等。
理解以下几点:
(1)图形中的每一个点都绕旋转中心旋转了同样大小的角度。
(2)对应点到旋转中心的距离相等,对应线段相等,对应角相等。
(3)图形的大小与形状都没有发生改变,只改变了图形的位置。
【考点7 利用旋转的性质求解】
【例7】(2022春•梅州校级模拟预测)如图,点O是等边△ABC内一点,∠AOB=110°,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,若OD=AD,则∠BOC的度数为 140° .
【分析】设∠BOC=α,根据旋转前后图形不发生变化,易证△COD是等边△OCD,从而利用α分别表示出∠AOD与∠ADO,再根据等腰△AOD的性质求出α.
【解答】解:设∠BOC=α,根据旋转的性质知,△BOC≌△ADC,则OC=DC,∠BOC=∠ADC=α.
又∵△BOC绕点C按顺时针方向旋转60°得到△ADC,
∴∠OCD=60°,
∴△OCD是等边三角形,
∴∠COD=∠CDO=60°,
∵OD=AD,
∴∠AOD=∠DAO.
∵∠AOD=360°﹣110°﹣60°﹣α=190°﹣α,∠ADO=α﹣60°,
∴2×(190°﹣α)+α﹣60°=180°,
解得α=140°.
故答案是:140°.
【变式7-1】(2022•东莞市校级一模)如图,△AOB中,∠AOB=90°,AO=4,BO=8,△AOB绕点O逆时针旋转到△A′OB′处,此时线段A′B′与BO的交点E为BO的中点,则线段B′E的长度为( )
A.35B.1255C.955D.1655
【分析】由勾股定理求出AB,由旋转的性质可得AO=A′O,A′B′=AB,再求出OE,从而得到OE=A′O,过点O作OF⊥A′B′于F,由三角形的面积求出OF,由勾股定理列式求出EF,再由等腰三角形三线合一的性质可得A′E=2EF,然后由B′E=A′B′﹣A′E代入数据计算即可得解.
【解答】解:∵∠AOB=90°,AO=4,BO=8,
∴AB=AO2+BO2=42+82=45,
∵△AOB绕顶点O逆时针旋转到△A′OB′处,
∴AO=A′O=4,A′B′=AB=45,
∵点E为BO的中点,
∴OE=12BO=12×8=4,
∴OE=A′O=4,
过点O作OF⊥A′B′于F,如图,
S△A′OB′=12×45•OF=12×4×8,
解得:OF=855,
在Rt△EOF中,EF=OE2−OF2=42−(855)2=455,
∵OE=A′O,OF⊥A′B′,
∴A′E=2EF=2×455=855,
∴B′E=A′B′﹣A′E=45−855=1255.
故选:B.
【变式7-2】(2022•城步县模拟)如图,P为等边三角形ABC内一点,∠APB:∠APC:∠CPB=5:6:7,则以PA,PB,PC为三边构成的三角形的三个内角从小到大的度数之比为( )
A.1:2:3B.2:3:4C.3:4:5D.5:6:7
【分析】将△APB绕A点逆时针旋转60°得△ADC,显然有△ADC≌△APB,连PD,则AD=AP,∠DAP=60°,得到△ADP是等边三角形,PD=AP,所以△DCP的三边长分别为PA,PB,PC;再由∠APB+∠BPC+∠CPA=360°,∠APB:∠APC:∠CPB=5:6:7,得到∠APB=100°,∠BPC=140°,∠CPA=120°,这样可分别求出∠PDC=∠ADC﹣∠ADP=∠APB﹣∠ADP=100°﹣60°=40°,∠DPC=∠APC﹣∠APD=120°﹣60°=60°,∠PCD=180°﹣(40°+60°)=80°,即可得到答案.
【解答】解:如图,将△APB绕A点逆时针旋转60°得△ADC,
显然有△ADC≌△APB,连PD,
∵AD=AP,∠DAP=60°,
∴△ADP是等边三角形,
∴PD=AP,
∵DC=PB,
∴△DCP的三边长分别为PA,PB,PC,
∵∠APB+∠BPC+∠CPA=360°,∠APB:∠APC:∠CPB=5:6:7,
∴∠APB=100°,∠BPC=140°,∠CPA=120°,
∴∠PDC=∠ADC﹣∠ADP=∠APB﹣∠ADP=100°﹣60°=40°,
∠DPC=∠APC﹣∠APD=120°﹣60°=60°,
∠PCD=180°﹣(40°+60°)=80°,
∴以PA,PB,PC为三边构成的三角形的三个内角从小到大的度数之比为2:3:4.
故选:B.
【变式7-3】(2022春•和平区模拟预测)如图,△ABC与△CDE都是等边三角形,连接AD,BE,CD=4,BC=2,若将△CDE绕点C顺时针旋转,当点A、C、E在同一条直线上时,线段BE的长为( )
A.23B.27C.3或7D.23或27
【分析】分两种情况:①当E在CA延长线上时,过A作AM⊥BE于M,根据△ABC与△CDE都是等边三角形,CD=4,BC=2,可得AE=AB,∠AEB=∠ABE=30°,在Rt△ABM中,可得BM=3,从而BE=2BM=23;②当E在AC的延长线上时,过B作BN⊥AC于N,在Rt△BCN中,CN=12BC=1,BN=3CN=3,在Rt△BNE中,BE=BN2+NE2=27.
【解答】解:①当E在CA延长线上时,过A作AM⊥BE于M,如图:
∵△ABC与△CDE都是等边三角形,CD=4,BC=2,
∴AE=CE﹣AC=4﹣2=2,∠BAC=60°,
∴AE=AB,
∴∠AEB=∠ABE=30°,
在Rt△ABM中,
AM=12AB=1,BM=3AM=3,
∴BE=2BM=23;
②当E在AC的延长线上时,过B作BN⊥AC于N,如图:
在Rt△BCN中,
CN=12BC=1,BN=3CN=3,
∴NE=CE+CN=4+1=5,
在Rt△BNE中,
BE=BN2+NE2=(3)2+52=27;
综上所述,线段BE的长为23或27,
故选:D.
【考点8 旋转中的坐标与图形变换】
【例8】(2022秋•黄石模拟预测)如图,线段AB与线段CD关于点P对称,若点A(a,b)、B(5,1)、D(﹣3,﹣1),则点C的坐标为( )
A.(﹣a,﹣b)B.(﹣a+2,﹣b)
C.(﹣a﹣1,﹣b+1)D.(﹣a+1,﹣b﹣1)
【分析】运用中点坐标公式求答案.
【解答】解:设C(m,n),
∵线段AB与线段CD关于点P对称,
点P为线段AC、BD的中点.
∴a+m2=5−32,b+n2=1−12,
∴m=2﹣a,n=﹣b,
∴C(2﹣a,﹣b),
故选:B.
【变式3-1】(2022秋•本溪模拟预测)如图,在△AOB中,OA=4,OB=6,AB=27,将△AOB绕原点O逆时针旋转90°,则旋转后点A的对应点A′的坐标是( )
A.(﹣4,2)B.(﹣23,4)C.(﹣23,2)D.(﹣2,23)
【分析】如图,过点A作AH⊥OB于H,设OH=m,则BH=6﹣m,利用勾股定理构建方程求出m,可得结论.
【解答】解:如图,过点A作AH⊥OB于H,设OH=m,则BH=6﹣m,
∵AH2=OA2﹣OH2=AB2﹣BH2,
∴42﹣m2=(27)2﹣(6﹣m)2,
∴m=2,
∴AH=42−22=23,
∴A(2,23),
∴将△AOB绕原点O逆时针旋转90°,则旋转后点A的对应点A′(﹣23,2),
【变式3-2】(2022秋•西湖区模拟预测)如图,在平面直角坐标系中,△MNP绕原点逆时针旋转90°得到△M1N1P1,若M(1,﹣2),则点M1的坐标为( )
A.(﹣2,﹣1)B.(1,2)C.(2,1)D.(﹣1,﹣2)
【分析】如图,连接OM,OM1,过点M作MH⊥y轴于点H,过点M1作M1T⊥x轴于点T.利用全等三角形的性质解决问题即可.
【解答】解:如图,连接OM,OM1,过点M作MH⊥y轴于点H,过点M1作M1T⊥x轴于点T.
∵M(1,﹣2),
∴MH=1,OH=2,
∵∠MOM1=∠POT,
∴∠MOH=∠M1OT,
∵∠MHO=∠M1TO=90°,OM=OM1,
∴△MHO≌△M1TO(AAS),
∴MH=M1T=1,OH=OT=2,
∴M1(2,1),
故选:C.
【变式3-3】(2022•新抚区模拟)如图,Rt△AOB的斜边AO在y轴上,OB=3,∠AOB=30°,直角顶点B在第二象限,将Rt△AOB绕原点O顺时针旋转120°后得到△A′OB',则A点的对应点A′的坐标是( )
A.(3,﹣1)B.(1,−3)C.(2,0)D.(3,0)
【分析】如图,利用含30度的直角三角形三边的关系得到BC=1,再利用旋转的性质得到OB′=OB=3,B′A′=BA=1,∠A′B′O=∠ABO=90°,然后利用第四象限点的坐标特征写出点A′的坐标.
【解答】解:如图,
在Rt△OAB中,∵∠BOA=30°,
∴AB=33OB=33×3=1,
∵Rt△OCB绕原点顺时针旋转120°后得到△OA′B',
∴OB′=OB=3,B′A′=BA=1,∠A′B′O=∠ABO=90°,
∴点A′的坐标为(3,﹣1).
故选:A.
【考点9 位似变换】
【例9】(2022春•如皋市模拟预测)若△ABC绕点A逆时针旋转α后,与△ADE构成位似图形,则我们称△ABC与△ADE互为“旋转位似图形”.
(1)知识理解:
如图1,△ABC与△ADE互为“旋转位似图形”.
①若α=25°,∠D=100°,∠C=28°,则∠BAE= ;
②若AD=6,DE=7,AB=4,则BC=
(2)知识运用:
如图2,在四边形ABCD中,∠ADC=90°,AE⊥BD于点E,∠DAC=∠DBC,求证:△ACD与△ABE互为“旋转位似图形”.
(3)拓展提高:
如图3,△ABG为等边三角形,点C为AG的中点,点F是AB边上的一点,点D为CF延长线上的一点,点E在线段CF上,且△ABD与△ACE互为“旋转位似图形”.若AB=6,AD=4,求DECE的值.
【答案】(1)①27°;②143;(2)见解析; (3)2155.
【分析】(1)①依据△ABC和△ADE互为“旋转位似图形”,可得△ABC∽△ADE,依据相似三角形的对应角相等,即可得到∠BAE=180°﹣100°﹣28°﹣25°=27°;
②依据△ABC∽△ADE,可得BCDE=ABAD,根据AD=6,DE=7,AB=4,即可得出BC=143;
(2)依据△AOD∽△BOC,即可得到AODO=BOCO,进而得到△AOB∽△DOC,再根据∠7=∠8,∠ADC=∠AEB,即可得到△ABE∽△ACD,进而得出△ACD和△ABE互为“旋转位似图形”;
(3)利用三角函数和勾股定理解答即可.
【详解】(1)①∵△ABC和△ADE互为“旋转位似图形”,
∴△ABC∽△ADE,
∴∠D=∠B=100°,
又∵α=25°,∠E=28°,
∴∠BAE=180°﹣100°﹣25°﹣28°=27°;
②∵△ABC∽△ADE,
∴BCDE=ABAD,
∵AD=6,DE=7,AB=4,
∴BC7=46,
∴BC=143,
故答案为:27°;143;
(2)∵∠DOA=∠COB,∠DAC=∠DBC,
∴△DOA∽△COB,
∴AOBO=DOCO,即AODO=BOCO,
又∵∠DOC=∠AOB,
∴△AOB∽△DOC,
∴∠DCA=∠EBA,
又∵∠ADC=90°,AE⊥BD,
∴∠ADC=∠AEB=90°,
∴△ABE∽△ACD,
∴∠DAC=∠EAB,
∴△AEB绕点A逆时针旋转∠DAE的度数后与△ADC构成位似图形,
∴△ACD和△ABE互为“旋转位似图形”;
(3)∵AC=12AG=12AB=3,
由题意得:ECBD=ACAB=AEAD=12,
∵AD=4,
∴AE=2,
∵∠DAE=∠FAC=60°,
∴cs∠DAE=cs60°=12,
∴∠DEA=90°,
∴由勾股定理可得CE=AC2−AE2=32−22=5,
∴DE=AE•tan∠DAE=23,
∴DECE=235=2155.
【点睛】本题属于相似形综合题,主要考查了相似三角形的判定及性质,等腰直角三角形的判定及性质,勾股定理的综合运用.在解答时添加辅助线等腰直角三角形,利用相似形的对应边成比例是关键.
【变式9-1】(2022·山东潍坊·中考真题)《墨子·天文志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形ABCD的面积为4,以它的对角线的交点为位似中心,作它的位似图形A′B′C′D′,若A′B′:AB=2:1,则四边形A′B′C′D′的外接圆的周长为___________.
【答案】42π
【分析】根据正方形ABCD的面积为4,求出AB=2,根据位似比求出A′B′=4,周长即可得出;
【详解】解:∵正方形ABCD的面积为4,
∴ AB=2,
∵ A′B′:AB=2:1,
∴ A′B′=4,
∴ A′C′=42+42=42,
所求周长=42π;
故答案为:42π.
【点睛】本题考查位似图形,涉及知识点:正方形的面积,正方形的对角线,圆的周长,解题关键求出正方形ABCD的边长.
【变式9-2】(2022·贵州黔西·中考真题)如图,△A′B′C′与△ABC是位似图形,点O为位似中心,若OA′=A′A,则△A′B′C′与△ABC的面积比为__.
【答案】1:4
【分析】根据位似图形的性质得出△ABC∽△A'B'C'和相似比的值,然后根据相似三角形的性质面积比是相似比比值的平方解答即可.
【详解】解:由题意得,△ABC和△A'B'C'是位似图形,
∴△ABC∽△A'B'C',AB:A'B'=OA:AA'=1:2,
∴△A′B′C′与△ABC的面积比为:1:4.
故答案为:1:4.
【点睛】此题考查的知识点为:位似的概念、三角形相似的性质;掌握面积比是相似比比值的平方是解答问题的关键.
【变式9-3】(2022·安徽·中考真题)如图,在由边长为1个单位长度的小正方形组成的10×10网格中,已知点O,A,B均为网格线的交点.
(1)在给定的网格中,以点O为位似中心,将线段AB放大为原来的2倍,得到线段A1B1(点A,B的对应点分别为A1、B1).画出线段A1B1;
(2)将线段A1B1绕点B1逆时针旋转90°得到线段A2B1.画出线段A2B1;
(3)以A、A1、B1、A2为顶点的四边形AA1B1A2的面积是_______个平方单位.
【答案】(1)画图见解析;(2)画图见解析;(3)20
【分析】(1)结合网格特点,连接OA并延长至A1,使OA1=2OA,同样的方法得到B1,连接A1B1即可得;
(2)结合网格特点根据旋转作图的方法找到A2点,连接A2B1即可得;
(3)根据网格特点可知四边形AA1 B1A2是正方形,求出边长即可求得面积.
【详解】(1)如图所示;
(2)如图所示;
(3)结合网格特点易得四边形AA1 B1A2是正方形,
AA1=42+22=25,
所以四边形AA1 B1A2的面积为:252=20,
故答案为:20.
【点睛】本题考查了作图-位似变换,旋转变换,能根据位似比、旋转方向和旋转角得到关键点的对应点是作图的关键.
【考点10 图形的变换与作图】
【例10】(2022春•化州市校级一模)如图,在平面直角坐标系中,△ABC的三个顶点分别是A(1,3),B(4,4),C(2,1).
(1)把△ABC向左平移4个单位后得到对应的△A1B1C1,请画出平移后的△A1B1C1;
(2)把△ABC绕原点O旋转180°后得到对应的△A2B2C2,请画出旋转后的△A2B2C2.
【分析】(1)利用平移变换的性质分别作出A,B,C的对应点A1,B1,C1即可;
(2)利用旋转变换的性质分别作出A,B,C的对应点A2,B2,C2即可.
【解答】解:(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求.
【变式10-1】(2022春·北京怀柔·九年级模拟预测)如图,在平面直角坐标系中,三角形ABC的三个顶点分别是A(0,4),B(-4,1),C(-1,2).
请你解答下列问题:
(1)在平面直角坐标系中画出三角形ABC;
(2)将三角形ABC先向下平移5个单位,再向右平移3个单位.画出平移后的三角形A1B1C1.
(3)把(2)三角形A1B1C1各个顶点的横坐标保持不变,纵坐标增加2,得到三角形A2B2C2.直接写出三角形A2B2C2的面积.
【答案】(1)作图见解析;
(2)作图见解析;
(3)作图见解析;2.5
【分析】(1)利用点A、B、C的坐标描点连线即可;
(2)利用点的坐标变换规律得到的坐标A1、B1、C1,然后描点连线即可;
(3)把点A1、B1、C1的横坐标保持不变,纵坐标增加2得到A2、B2、C2的坐标,再描点连线得到△A2B2C2,然后用一个大直角三角形的面积分别减去2个小直角三角形的面积和一个正方形的面积去计算△A2B2C2的面积.
(1)
如图,△ABC为所作;
(2)
如图,△A1B1C1为所作;
(3)
如图,△A2B2C2为所作,
△A2B2C2的面积=12×3×4−12×3×1−12×2×1-1×1=2.5.
【点睛】本题考查了作图−平移变换:作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
【变式10-2】(2022·广西桂林·中考真题)如图,在平面直角坐标系中,形如英文字母“V”的图形三个端点的坐标分别是A(2,3),B(1,0),C(0,3).
(1)画出“V”字图形向左平移2个单位后的图形;
(2)画出原“V”字图形关于x轴对称的图形;
(3)所得图形与原图形结合起来,你能从中看出什么英文字母?(任意答一个即可)
【答案】(1)见解析
(2)见解析
(3)图1是W,图2是X
【分析】(1)根据要求直接平移即可;
(2)在第四象限画出关于x轴对称的图形;
(3)观察图形可得结论.
【详解】(1)解:如图所示,将点A(2,3),B(1,0),C(0,3)得A′(0,3),B′(−1,0),C′(−2,3),
(2)解:如图所示,
(3)解:图1是W,图2是X.
【点睛】本题考查了对称的性质和平移,解题关键是牢固掌握关于坐标轴对称的点的坐标的特征并能灵活运用.
【变式10-3】(2022春•蒲城县模拟预测)在如图所示的平面直角坐标系中,每个小方格都是边长为1个单位长度的正方形,△ABC的顶点坐标分别为A(1,1),B(3,0),C(2,3).
(1)将△ABC向左平移4个单位长度得到△A1B1C1,点A、B、C的对应点分别为A1、B1、C1,请画出△A1B1C1,并写出点C1的坐标;
(2)以原点O为旋转中心,将△ABC顺时针旋转90°得到△A2B2C2,点A、B、C的对应点分别为A2、B2、C2,请画出△A2B2C2.
【分析】(1)利用平移变换的性质分别作出A,B,C的对应点A1,B1,C1即可;
(2)利用旋转变换的性质分别作出A,B,C的对应点A2,B2,C2即可.
【解答】解:(1)如图,△A1B1C1即为所求,点C1的坐标(﹣2,3);
(2)如图,△A2B2C2即为所求.
相关试卷
这是一份中考数学总复习举一反三系列(通用版)专题25投影与视图(10个高频考点)(全国通用)(原卷版+解析),共35页。
这是一份中考数学总复习举一反三系列(通用版)专题24尺规作图(10个高频考点)(全国通用)(原卷版+解析),共61页。
这是一份中考数学总复习举一反三系列(通用版)专题23与圆有关的计算(10个高频考点)(强化训练)(全国通用)(原卷版+解析),共60页。









