2023-2024学年北京市清华附中奥森分校高二（上）期中数学试卷

这是一份2023-2024学年北京市清华附中奥森分校高二（上）期中数学试卷，共6页。试卷主要包含了选择题等内容，欢迎下载使用。
1．已知空间两点A（2，1，1），B（3，2，1），下列选项中的与共线的是（ ）
A．＝（1，0，1）B．＝（2，1，1）
C．＝（2，﹣2，0）D．＝（2，2，0）
2．已知直线m，直线n和平面α，则下列四个命题中正确的是（ ）
A．若m∥/α，n⊂α，则m∥nB．若m∥α，n∥α，则m∥n
C．若m⊥α，n∥α，则m⊥nD．若m⊥n，n∥α，则m⊥α
3．若数组＝（﹣2，1，3）和，，x）满足，则实数x等于（ ）
A．﹣3B．﹣2C．D．
4．若{}是空间的一个基底，则下列各组中不能构成空间一个基底的是（ ）
A．B．，，
C．，，D．，
5．如图，空间四边形OABC 中，，，，点M，N分别为OA，BC的中点，则＝（ ）
A．B．
C．D．
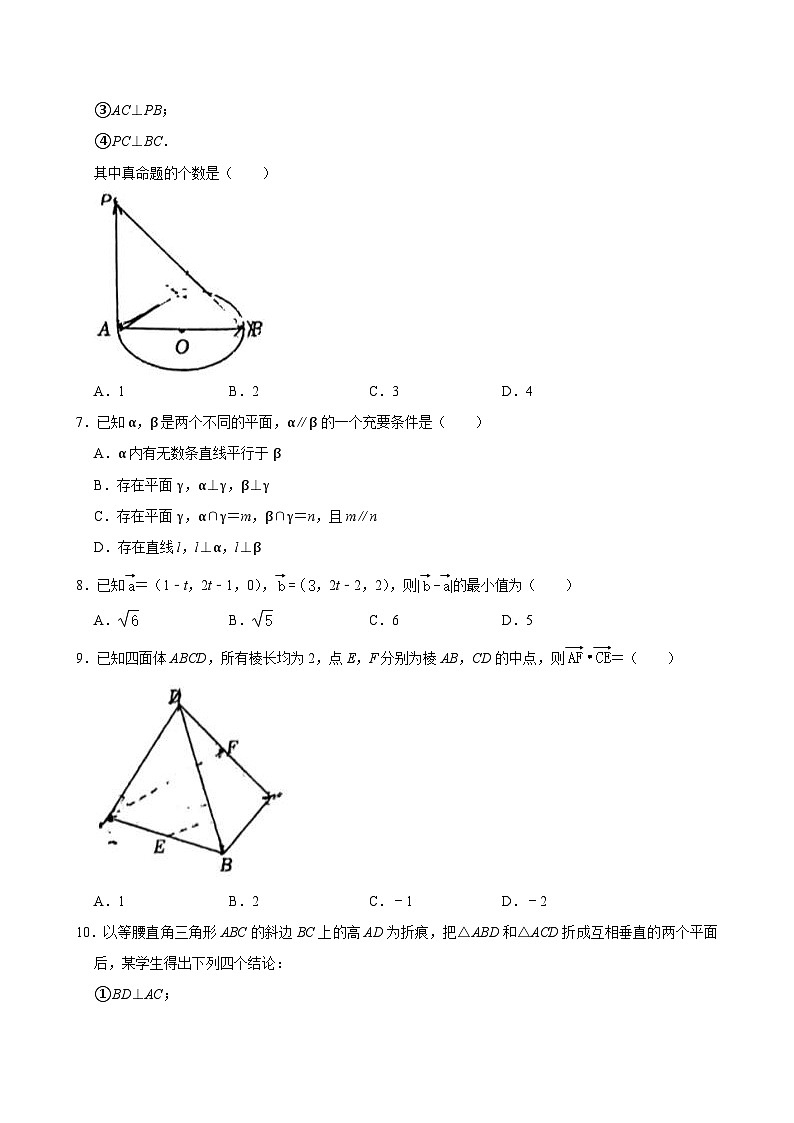
6．如图，PA垂直于以AB为直径的圆O所在的平面，C为圆上异于A、B的任一点，现有下列命题：
①PA⊥BC；
②BC⊥平面PAC；
③AC⊥PB；
④PC⊥BC．
其中真命题的个数是（ ）
A．1B．2C．3D．4
7．已知α，β是两个不同的平面，α∥β的一个充要条件是（ ）
A．α内有无数条直线平行于β
B．存在平面γ，α⊥γ，β⊥γ
C．存在平面γ，α∩γ＝m，β∩γ＝n，且m∥n
D．存在直线l，l⊥α，l⊥β
8．已知＝（1﹣t，2t﹣1，0），，2t﹣2，2），则||的最小值为（ ）
A．B．C．6D．5
9．已知四面体ABCD，所有棱长均为2，点E，F分别为棱AB，CD的中点，则＝（ ）
A．1B．2C．﹣1D．﹣2
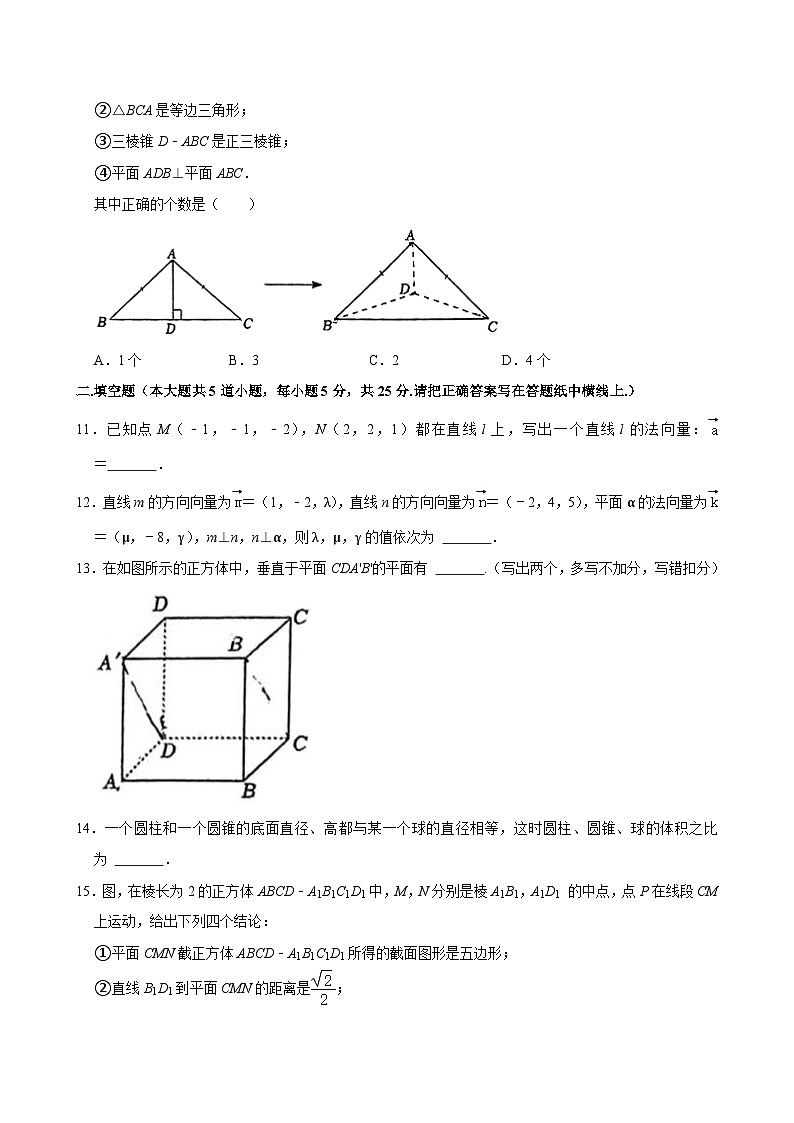
10．以等腰直角三角形ABC的斜边BC上的高AD为折痕，把△ABD和△ACD折成互相垂直的两个平面后，某学生得出下列四个结论：
①BD⊥AC；
②△BCA是等边三角形；
③三棱锥D﹣ABC是正三棱锥；
④平面ADB⊥平面ABC．
其中正确的个数是（ ）
A．1个B．3C．2D．4个
二.填空题（本大题共5道小题，每小题5分，共25分.请把正确答案写在答题纸中横线上.）
11．已知点M（﹣1，﹣1，﹣2），N（2，2，1）都在直线l上，写出一个直线l的法向量：＝ ．
12．直线m的方向向量为＝（1，﹣2，λ），直线n的方向向量为＝（﹣2，4，5），平面α的法向量为＝（μ，﹣8，γ），m⊥n，n⊥α，则λ，μ，γ的值依次为 ．
13．在如图所示的正方体中，垂直于平面CDA'B'的平面有 .（写出两个，多写不加分，写错扣分）
14．一个圆柱和一个圆锥的底面直径、高都与某一个球的直径相等，这时圆柱、圆锥、球的体积之比为 ．
15．图，在棱长为2的正方体ABCD﹣A1B1C1D1中，M，N分别是棱A1B1，A1D1 的中点，点P在线段CM上运动，给出下列四个结论：
①平面CMN截正方体ABCD﹣A1B1C1D1所得的截面图形是五边形；
②直线B1D1到平面CMN的距离是；
③存在点P，使得∠B1PD1＝90°；
④△PDD1面积的最小值是．
其中所有正确结论的序号是 ．
三.解答题（本大题共6道小题，共85分，解答应写出文字说明，证明过程或演算步骤）.
16．已知向量．
（1）求；
（2）若向量与垂直，求实数k的值；
17．如图，△ABC中，AC＝BC＝1，，ABED是正方形，平面ABED⊥平面ABC，若G、F分别是EC、BD的中点．
（1）求证：GF∥平面ABC；
（2）求证：平面BCE⊥平面ACD．
18．如图，在四棱锥P﹣ABCD中，底面ABCD为正方形，PD⊥平面ABCD，PD＝AB，点E，F，G分别为PC，PA，BC的中点．
（1）求证：PB⊥EF；
（2）求平面EFG与平面PAD所成二面角D﹣FG﹣E（锐角）的余弦值．
19．如图，在直三棱柱ABC﹣A1B1C1中，∠ACB＝90°，AC＝CB＝CC1＝2，E是AB中点．
（1）求证：AB1⊥平面A1CE；
（2）求直线 A1C1与平面A1CE所成角的正弦值．
20．如图，在四棱锥P﹣ABCD中，PD⊥平面ABCD，底面ABCD为菱形，E，F分别为AB，PD的中点．
（1）求证：EF∥平面PBC；
（2）若，二面角E﹣FC﹣D的大小为45°，再从条件①、条件②这两个条件中选择一个作为已知，求PD的长．
条件①：DE⊥PC；
条件②：PB＝PC．
21．记所有非零向量构成的集合为V，对于，，，定义V（，）＝{∈V|•＝•}．
（1）若 ，，求出集合V（，）中的三个元素；
（2）若V（，）＝V（，），其中，求证：一定存在实数λ1，λ2，且λ1+λ2＝1，使得．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2024/7/17 10:07:47；用户：笑涵数学；邮箱：15699920825；学号：36906111