人教B版 (2019)必修 第四册10.1.2 复数的几何意义优秀ppt课件

这是一份人教B版 (2019)必修 第四册10.1.2 复数的几何意义优秀ppt课件，共19页。PPT课件主要包含了数轴上的点，一一对应，复数的一般形式，复数与点的对应，x轴实轴，y轴虚轴，复平面，探究点2共轭复数，共轭复数定义，代数形式等内容，欢迎下载使用。

在几何上，我们用什么来表示实数?
实数可以用数轴上的点来表示.
类比实数的表示，可以用什么来表示复数？
1.理解复数与以原点为起点的向量的对应关系. （重点）2.了解复数的几何意义.（难点）3.会用复数的几何意义解决有关问题.
探究点1 复数的几何意义（一）
z=a+bi(a, b∈R)
思考1：一个复数由什么唯一确定？
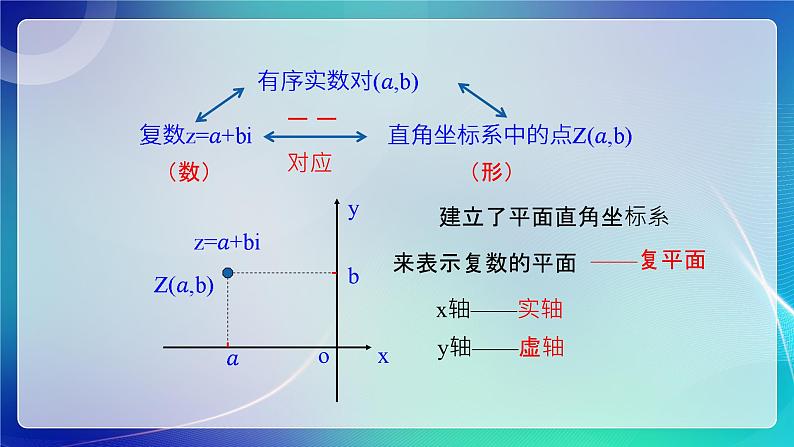
建立了平面直角坐标系来表示复数的平面
思考1：设 3 + i 与 3 – i 在复平面内对应的点分别为 A 与 B，在复平面内画出点 A，B，并说说两点的位置关系是怎样的？
A，B 两点关于实轴对称
如图，在复平面内，表示两个共轭复数的点关于实轴对称；反之，如果表示两个复数的点在复平面内关于实轴对称，则这两个复数互为共轭复数.
探究点3 复数的几何意义（二）
思考：在复平面内，复数除了用点来表示，还可以用什么来表示呢？
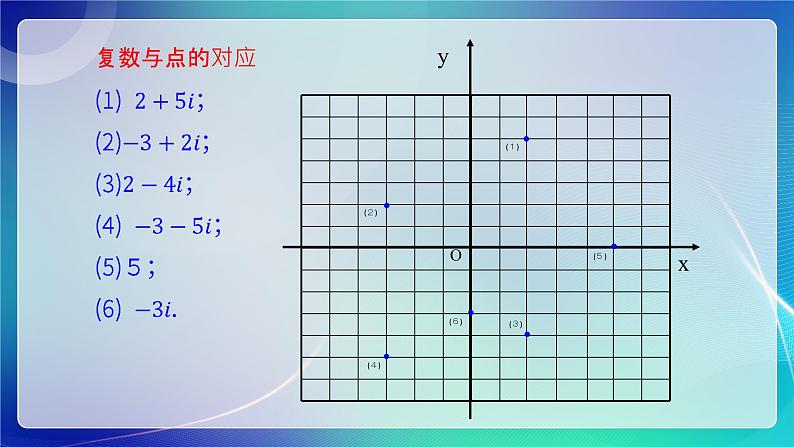
1.写出图中的各点表示的复数. 2.在复平面内，作出表示下列复数的点和向量： 3-i,4+i,7,i,6-4i,-1+4i.
解：1.A:3+4i,B:2+i,C:-5+i,D:-1-i；
2.如图所示，A:3-i,B:4+i,C:7,D:i,E:6-4i,F:-1+4i.
实数绝对值的几何意义:
实数a在数轴上所对应的点A到原点O的距离.
复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离.
设复数 z 在复平面内对应的点为 Z，说明当 z 分别满足下列条件时，点 Z 组成的集合是什么图形，并作图表示.（1）| z | = 2； （2）1 < | z | ≤ 3.